斐波那契数列

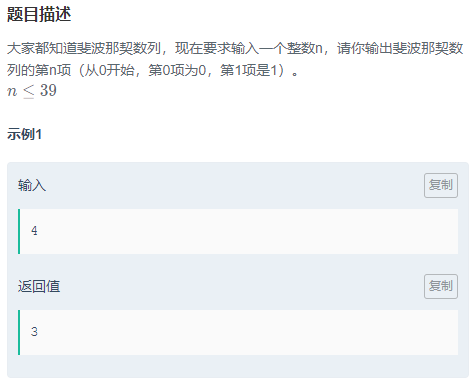
题目：

 

 

 

思路：

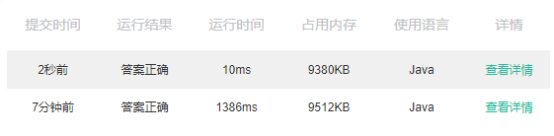
斐波那契数列的核心就是F(N) = F(N-1) + F(N-2)，一般看到的都会采用递归，但是如果使用循环来实现且进行对比，容易发现不少对真是性能的影响

 

如上面的采用循环运行时间大大的小于下面用递归实现的运行时间。这种有点类似于插入排序算法的不同实现，每次都换位置的话效率如同冒泡，但是可以一次性比较完后在进行插入，减少了对变量操作。

代码示例：

public class Solution {

    public static void main(String[] args) {

        System.out.println(Fibonacci2(4));

    }

 

    /**

     * 采用循环实现斐波那契数列，即F(N) = F(N-1) + F(N-2),比递归要更节省时间，原因在于，如果调用层数比较深，每次都要创建新的变量，

     * 需要增加额外的堆栈处理，会对执行效率有一定影响，占用过多的内存资源。

     * 在递归调用的过程中系统为每一层的返回点、局部变量等开辟了栈来储存。递归次数过多容易造成栈溢出

     *

     * @param n

     * @return

     */

    public static int Fibonacci2(int n) {

        int a = 0, b = 1, result = 0;

        if (n < 0)

            return -1;

        if (n == 0)

            return a;

        if (n == 1)

            return b;

        for (int i = 2; i <= n; i++) {

            result = a + b;

            a = b;

            b = result;

        }

        return result;

    }

 

    public static int Fibonacci1(int n) {

        int a = 0, b = 1;

        if (n < 0)

            return -1;

        if (n == 0)

            return a;

        if (n == 1)

            return b;

        return Fibonacci1(n - 1) + Fibonacci1(n - 2);

    }

 

 

}