UOJ Easy Round#7

UOJ Easy Round#7

传送门：http://uoj.ac/contest/35

题解：http://matthew99.blog.uoj.ac/blog/2085

题意：

在一个（2n+1）*(2n+1)的网格中，每次只能走到相邻的点，

从左上端出发到右下端，找到一条路径，使此路径经过的所有点权值和最小。

输入：从内到外输出每一圈的点值大小；数据范围n<=10^5；

比赛中：

拿到题目，看到那极有特色性的一个大方格，以及极为特殊的走法，和那10^5的数据量，算法上基本可以确定贪心；

根据直觉，知道最短路径肯定是从左上角绕到某里圈一层的左上角，然后再从里圈的左上角沿着路线走到这一圈的右下角，然后再按照对称性跑到右下角；

关键是如何使从左上角到里圈左上角的路径最短，我同学提出了很多方法，但大多的问题是有后效性，或者是会Tle；

找不到思路后，我决定按照直觉敲n^2dp；

实际得分：50分；

题意:给定一个长度为n的序列，输出所有的ans使

k∈[2,n]，ans=min{MAXi-MINi}i∈所有长度为k的区间；

且如果答案与标准答案相差不超过5%，也算做正确；（吐槽：近似算法都出出来了，这真的是noip难度吗？）

比赛中：关键信息是题目中允许近似这一点上，做过bzoj遥远的行星这题的估计都对近似有些印象；

在开始考虑如何近似之后，我发现很难做，基本无思路；

但50%的数据比较好搞，两个for循环搞定；

实际得分：50分；

题意：求最大的ans=max(s(l,r)*(r-l))

s(l,r)表示l到r这个区间之间所有数之间的最小的差的绝对值；

比赛中：此时已经心理崩溃，在看到这题没几个人交之后，决定放弃，思考前面的题目（尽管最后也没思考出什么结果）；

实际得分：0分

总体评价：在看完了题解之后，我发现这套题还真不是很难，至少都处于可写范围内：第一题贪心，第二题近似，第三题分块，而且算法都不是十分复杂，代码量都很小；

但为什么没做好，只搞到了100分呢？

一是没有清晰的思路,甚至于没有思路；

先说没有清晰的思路，第一题其实我们已经找到了切入点，极为明显的贪心痕迹和数据量帮助了我们；

我们已经知道了该如何做了，但是没有找到接下来的路（主要是没有解决后效性的问题）；

后来我看题解了后仔细思考了下，其实我的想法已经很接近答案了，但没有用画图，设未知数等方法进行仔细的分析，轻易放弃了；

再说没有思路，第二题第三题就属于这样，题中要求的信息很复杂，又是min，max又是区间之类的，这需要训练；

但也能大致发现这些题目中的一些规律：一般说来，对序列问题，分而治之是解决这些题目最有力方法，信息合并比较容易的话，可以考虑线段树之类的东西；如果信息合并不太容易，就像这次的第三题，合并一次O(n)，总的复杂度O(n^2)，这样的一般就需要考虑一下分块；

代码：

第一题：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<string>
#include<algorithm>
#include<ctime>
#include<cmath>
using namespace std;
#define LL long long 
#define up(i,j,n) for(int i=j;i<=n;i++)
#define down(i,n,j) for(int i=n;i>=j;i--)
const int maxn=101000;
int n;
int a[maxn];
LL ans=1LL<<62,minn=1LL<<62,sum=0;
int main(){
    scanf("%d",&n);n++;
    down(i,n,1)scanf("%d",&a[i]);
    up(i,1,n){
        minn=min(minn,(LL)a[i]);
        if(a[i]==minn)ans=min(ans,(sum<<1)+(4*(n-i)+1)*(LL)a[i]);
        sum+=minn+a[i];
    }
    printf("%lld\n",ans);
    return 0;
}

View Code

第二题：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<string>
#include<algorithm>
#include<ctime>
#include<cmath>
using namespace std;
#define LL long long 
#define up(i,j,n) for(int i=j;i<=n;i++)
#define down(i,n,j) for(int i=n;i>=j;i--)
const int maxn=101000,inf=1000000000;
namespace OI{
    const double c=1.05;
    int n;
    int a[maxn];
    int q[maxn],head=1,tail=0;
    int Q[maxn],Head=1,Tail=0;
    void slove(){
        scanf("%d",&n);
        up(i,1,n)scanf("%d",&a[i]);
        double L=1;
        for(int k=2;k<=n;k++){
            L*=c;
            int t=k+(int)L-1;
            if(t>n)t=n,L=t-k+1;
            int v=(k+t)>>1;
            int ans=inf;
            Head=1,Tail=0;head=1,tail=0;
            for(int i=1;i<=n;i++){
                while(head<=tail&&i-q[head]+1>v)head++;
                while(head<=tail&&a[q[tail]]<=a[i])tail--;
                q[++tail]=i;
                while(Head<=Tail&&i-Q[Head]+1>v)Head++;
                while(Head<=Tail&&a[Q[Tail]]>=a[i])Tail--;
                Q[++Tail]=i;
                if(i>=v)ans=min(ans,a[q[head]]-a[Q[Head]]);
            }
            up(i,1,(int)L)printf("%d\n",ans);
            k=t;
        }
        return;
    }
}
int main(){
    using namespace OI;
    slove();
    return 0;
}

View Code

第三题：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<string>
#include<algorithm>
#include<ctime>
#include<cmath>
using namespace std;
#define LL long long 
#define up(i,j,n) for(int i=j;i<=n;i++)
#define down(i,n,j) for(int i=n;i>=j;i--)
#define max(x,y) ((x)>(y)?(x):(y))
#define min(x,y) ((x)<(y)?(x):(y))
#define abs(x) ((x)<0?(-(x)):(x))
template<typename T>inline bool chkmax(T &a,T b){return a<b?a=b,true : false;}
template<typename T>inline bool chkmin(T &a,T b){return a>b?a=b,true : false;}
int read(){
    int x=0;char ch=getchar();bool flag=0;
    while(ch<'0'||ch>'9'){if(ch=='-')flag=1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return flag?-x:x;
}
namespace OI{
    const int maxn=201000,inf=1000000000;
    int n,m,k,S;
    LL ans=0;
    int a[maxn];
    int b[maxn<<1];
    int f[maxn];
    int now[maxn];
    void slove(){
        scanf("%d%d%d",&n,&m,&k);
        S=max(2,(int)sqrt(m*1.0)+1);
        up(i,1,n)a[i]=read();
        memset(f,127,sizeof(f));
        int mx=-1;
        for(int L=2;L<=S;++L){
            mx=-1;
            for(int i=1;i<=n-L+1;++i){
                chkmin(f[i],min(abs(a[i]-a[i+L-1]),f[i+1]));
                chkmax(mx,f[i]);
            }
            if(L>=k)chkmax(ans,(LL)mx*(L-1));
        }
        for(int i=1;i<=n;++i){
            for(int j=0;j<=S;++j){
                if(j&&i-now[j]>=k)chkmax(ans,(i-now[j]-1)*(LL)j);
                chkmax(now[j+1],now[j]);
                if(a[i]-j>0)chkmax(now[j+1],b[a[i]-j]);
                if(a[i]+j<=m)chkmax(now[j+1],b[a[i]+j]);
            }
            b[a[i]]=i;
        }
        printf("%lld\n",ans);
        return;
    }
}
int main(){
    using namespace OI;
    slove();
    return 0;
}

View Code

顺便说一句：常看看别人的代码是个好习惯，能get一些不错的技巧；

“；第七套广播体操，原地踏步——走！”

众所周知，跳蚤们最喜欢每天早起做早操，经常天还没亮就齐刷刷地站在操场做着反复纵跳热热身。跳晚国在研制三星 note7 的时候注意到了这点，于是他们打算让炸弹更快地引爆，这样就可以消灭更多早起的跳蚤。

三星 note7 的主板可以看作是由 $(2 n + 1) \times (2 n + 1)$ 个中继器构成的，某些中继器会有导线连在一起，左上角和右下角的中继器分别连着电源的正负极。

电流流过一根导线的时间可忽略不计，但当电流经过中继器时，会延缓一段时间再从中继器流出。这个时间只跟该中继器本身有关，我们把这段时间的长度称为中继器的延时值。

这些中继器由导线连接围成一个一个的层，同个层的中继器的种类都一样，而不同层的种类都不一样，可以发现总共有 $n + 1$ 层。当 $n = 4$ 时，主板大概长这样：

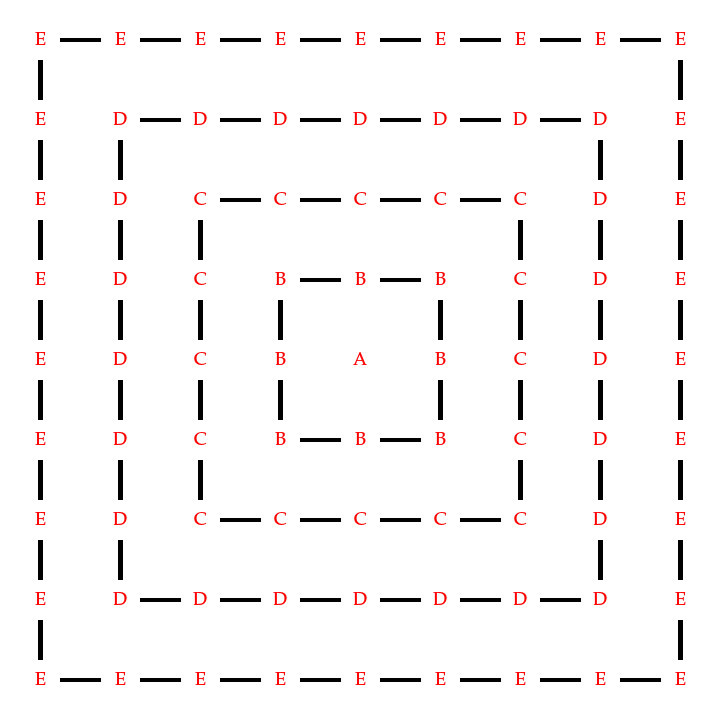
跳晚们打算再加几根导线将某些中继器连接起来.凭借发达的重工业，他们能生产出无数条导线。但由于主板的限制，他们的导线只能和主板四周的边平行，且其长度只够连接相邻两个中继器。

现在他们想知道，他们改造的三星 note7 的电源正极流出的电流能在多短的时间到达电源负极从而造成短路，这样电池就会释放出巨大的能量摧毁跳蚤国的有生力量了。

请参考输入格式和样例配图来更好地理解题意。

输入格式

第一行一个正整数 $n$ 。

第二行 $n + 1$ 个正整数 $a_{0}, a_{1}, \dots, a_{n}$ ，表示从内到外每层的中继器的延时值，单位为秒。其中，第 $i$ 行第 $j$ 列的中继器的延时值为（ $1 \leq i, j \leq n$ ）

a max (| i - n - 1 |, | j - n - 1 |)

输出格式

输出一行一个数表示改造后的最短引爆时间。

C/C++ 输入输出 long long 时请用 %lld。C++ 可以直接使用 cin/cout 输入输出。

posted @ 2016-10-19 17:54 CHADLZX 阅读(247) 评论(0) 编辑收藏举报

刷新页面返回顶部