拓扑排序

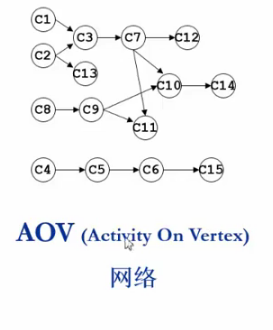
拓扑排序

• 拓扑序：如果图中从V到W有一条有向路径，则V一定排在W之前。满足此条件的顶点序列成为一个拓扑序
• 获得一个拓扑序的过程就是拓扑排序
• AOV如果有合理的拓扑序，则必定是有向无环图（Directed Acyclic Graph，DAG）

 

引入

　　如果

则称 a 为从 u 到 v 的弧(arc)，u和 v 为 a 的端点，称 u 是 a 的尾(tail)，v 是 a 的头(head)

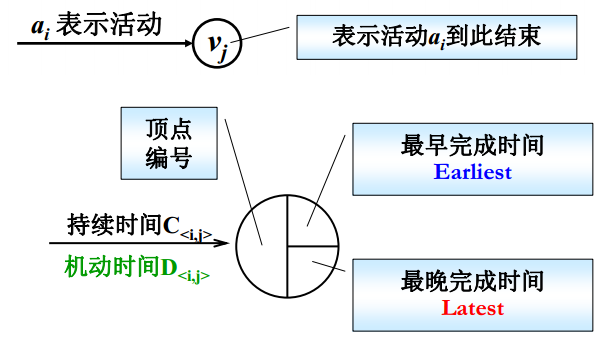
定义

　　顶点 v 的入度是指以 v 为头的弧的数目；顶点v的出度(outdere) 是指以 v 为尾的弧的数目。

 

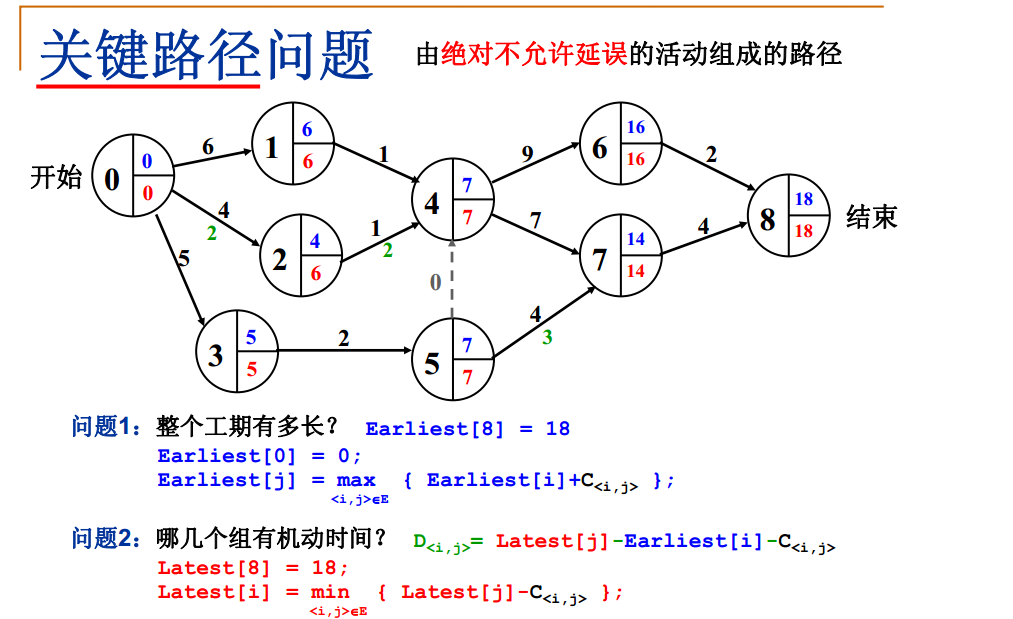
关键路径问题

AOE（Activity On Edge）网络

一般用于安排项目的工序

/* 邻接表存储 - 拓扑排序算法 */
 
bool TopSort( LGraph Graph, Vertex TopOrder[] )
{ /* 对Graph进行拓扑排序,  TopOrder[]顺序存储排序后的顶点下标 */
    int Indegree[MaxVertexNum], cnt;
    Vertex V;
    PtrToAdjVNode W;
       Queue Q = CreateQueue( Graph->Nv );
  
    /* 初始化Indegree[] */
    for (V=0; V<Graph->Nv; V++)
        Indegree[V] = 0;
         
    /* 遍历图，得到Indegree[] */
    for (V=0; V<Graph->Nv; V++)
        for (W=Graph->G[V].FirstEdge; W; W=W->Next)
            Indegree[W->AdjV]++; /* 对有向边<V, W->AdjV>累计终点的入度 */
             
    /* 将所有入度为0的顶点入列 */
    for (V=0; V<Graph->Nv; V++)
        if ( Indegree[V]==0 )
            AddQ(Q, V);
             
    /* 下面进入拓扑排序 */ 
    cnt = 0; 
    while( !IsEmpty(Q) ){
        V = DeleteQ(Q); /* 弹出一个入度为0的顶点 */
        TopOrder[cnt++] = V; /* 将之存为结果序列的下一个元素 */
        /* 对V的每个邻接点W->AdjV */
        for ( W=Graph->G[V].FirstEdge; W; W=W->Next )
            if ( --Indegree[W->AdjV] == 0 )/* 若删除V使得W->AdjV入度为0 */
                AddQ(Q, W->AdjV); /* 则该顶点入列 */ 
    } /* while结束*/
     
    if ( cnt != Graph->Nv )
        return false; /* 说明图中有回路, 返回不成功标志 */ 
    else
        return true;
}

 队列相关代码

#define ERROR -1
#define false  0
#define true   1

struct QNode {
    Vertex Data[MaxQueue];
    int rear;
    int front;
};
typedef struct QNode *Queue;

int IsEmptyQ(Queue PtrQ)
{
    return (PtrQ->front == PtrQ->rear);
}

void AddQ(Queue PtrQ, Vertex item)
{
    if((PtrQ->rear+1)%MaxQueue == PtrQ->front) {
        printf("Queue full");
        return;
    }
    PtrQ->rear = (PtrQ->rear+1)%MaxQueue;
    PtrQ->Data[PtrQ->rear] = item;
}

Vertex DeleteQ(Queue PtrQ)
{
    if(PtrQ->front == PtrQ->rear) {
        printf("Queue Empty");
        return -1;
    } else {
        PtrQ->front = (PtrQ->front+1)%MaxQueue;
        return PtrQ->Data[PtrQ->front];
    }
}