CodeForces 15C Industrial Nim 博弈论

 

题意：NIM博弈变形，第一行给出N表示有N个采石场，接下来N行每一行一个Xi一个Mi,表示第i个采石场有Mi量车，第1辆车的石头量是Xi，第二是Xi+1，第Mi辆车的石头的数量是Xi+Mi-1。有两个人玩nim博弈，可以去若干个，最后一个取完的赢，先手赢输出tolik，后手赢输出bolik。
思路：遍历所有的石头堆是不可能的，但你会发现每个采石场都是1个个递增的，这时假设石头量为n且n为偶数时，与n+1异或就会为1，再凑一对就为0，这时只要分类讨论加判断m%4即可。
初学NIM博弈的同学可以参考网址https://www.cnblogs.com/lengxia/p/4387859.html

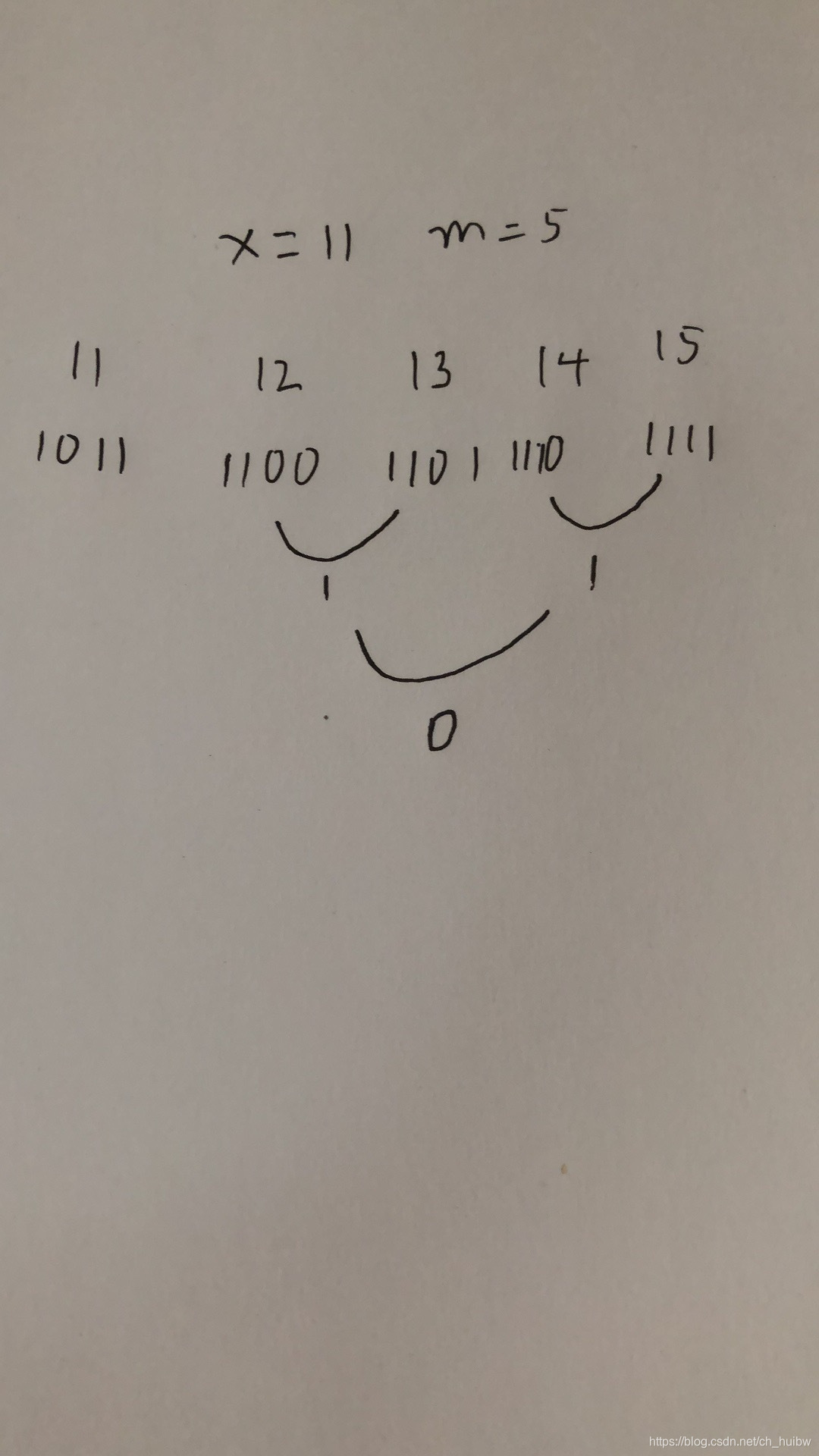
#include <iostream>
#include <algorithm>
using namespace std;
#define ll long long
#define N 1000005
ll x[N],m[N];
ll f(ll x,ll m)//x到x+m-1的石头堆
{
    ll i, j, k;
    ll ans;
    if (m & 1)//m为奇数个
    {
        if (x & 1)//若x为奇数，则后面的可以一起配对，因为n^(n+1)=1(n为偶数时，一定可以后面的数异或为1）,此时后面有(m/2)个1异或
            ans = x;
        else
            ans = x + m - 1;
        m--;//把x或者x+m-1
    }
    else//m为偶数个
    {
        if (x & 1)
        {
            ans = x ^ (x +m-1);//注意！不是x和x+1，因为x是奇数,配对完后只剩下x+m-1
            m -= 2;//除去x和x+m-1这俩个数
        }
        else
            ans = 0;//全部俩俩配对完毕
    }
    if (m % 4)//若不能配成偶数对即不能有偶数个1相异或的话
        return ans ^ 1;
    else
        return ans;
}
int main()
{
    ll i, j, k;
    ll n, t;
    ll sum = 0, ret = 0;
    ll ans = 0;
    cin >> n;
    for(i=0;i<n;i++)
    {
        cin >> x[i] >> m[i];
        ans ^= f(x[i], m[i]);
    }
        if (ans)
            cout << "tolik" << endl;
        else
            cout << "bolik" << endl;
}