二项分布

目录：

1. 定义
2. 期望与方差
3. 两个二项分布的协方差
4. python画图
5. 二项分布与其他分布的关系

一、定义

在n次独立重复的伯努利试验中，设每次试验中事件A发生的概率为p。用 X 表示n重伯努利试验中事件A发生的次数，则X的可能取值为0，1，…，n,且对每一个k（0≤k≤n）,事件{X=k}即为“n次试验中事件A恰好发生k次”，随机变量 X 的离散概率分布即为二项分布（Binomial Distribution）。

在概率论和统计学中，二项分布是n个独立的成功/失败试验中成功的次数的离散概率分布，其中每次试验的成功概率为p。这样的单次成功/失败试验又称为伯努利试验。实际上，当n=1时，二项分布就是伯努利分布

一般地，如果随机变量 X 服从参数为 n 和 p 的二项分布，我们记为 X~B(n,p)  或  X~b(n,p) 。n 次试验中正好得到 k 次成功的概率由概率质量函数给出：

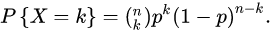
式中k=0，1，2...，n, 

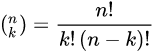
是二项分布，又记为C_n^k     该公式可以用以下方法理解：我们希望有k次成功(p)和n−k次失败(1 −p)。并且，k次成功可以在n次试验的任何地方出现，而把k次成功分布在n次试验中共有C_n^k   个不同的方法

 

二、期望与方差

如果 X~B(n,p)（也就是说，X是服从二项分布的随机变量），那么X的期望为：

 

 

X的方差为：

 

 

 

 

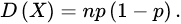
这个事实很容易证明。首先假设有一个伯努利试验。试验有两个可能的结果：1和0，前者发生的概率为p，后者的概率为1−p。该试验的期望值等于μ= 1 * p+ 0  * (1−p) =p。该试验的方差，也可以类似地计算：σ²= (1−μ)² p+ (0−μ)² (1−p) =p(1 − p)
一般的二项分布是n次独立的伯努利试验的和。它的期望值和方差分别等于每次单独试验的期望值和方差的和：

 

 

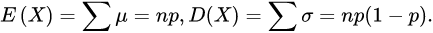
 三、两个二项分布的协方差

如果有两个服从二项分布的随机变量X和Y，我们可以求它们的协方差。利用协方差的定义，当n= 1时我们有：

 

 

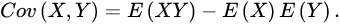
E(XY)为当X和Y都等于1时的概率，而E(X)和E(Y)分别为X= 1和Y= 1的概率。定义P,B为X和Y都等于1的概率，便得到：

 

 

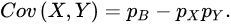
对于n次独立的试验，我们便有：

 

 

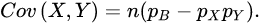
如果X和Y是相同的变量，便化为前文所述的的二项分布方差公式

 

 

四、python画图

import matplotlib.pyplot as plt
import numpy as np
from scipy import stats

#二项分布
n=100
p=0.3
k=np.arange(0,n)#生成一个0到N-1的数列
y1=stats.binom.pmf(k,n,p)
plt.plot(k,y1)
plt.show()

###画泊松分布的图
m=n*p
y2=stats.poisson.pmf(k,m)
plt.plot(k,y2,'g^-')
plt.show()

###再画个正态分布的图
l=np.sqrt(m)
y3=stats.norm.pdf(k,m,l)
plt.plot(k,y3,'ro-')
plt.show()

#画完三个图之后就把他们放一下对比一下吧,为了方便改变参数，我们把它写成一个函数吧。
def draw(times,possibility):
    import matplotlib.pyplot as plt
    import numpy as np
    from scipy import stats
    n=times
    p=possibility
    k=np.arange(0,n)#生成一个0到N-1的数列
    y1=stats.binom.pmf(k,n,p)
    m=n*p#确定泊松分布的参数
    y2=stats.poisson.pmf(k,m)
    l=np.sqrt(m)#确定正态分布的另一个参数
    y3=stats.norm.pdf(k,m,l)#注意一下前两个是pmf最后一个是pdf
    plt.xlabel('k')
    plt.ylabel('possibility')
    plt.title('three distribution :n=%d  p=%.2f' % (n,p) )#用到了python的格式化
    binomial=plt.plot(k,y1,color='r',label='binomial')
    poisson=plt.plot(k,y2,color='g',label='poisson')
    normal=plt.plot(k,y3,color='b',label='normal')#对图的参数进行调整
    plt.legend(loc='upper right')#把图例放在右上角
    plt.show()

draw(100,0.3)

 

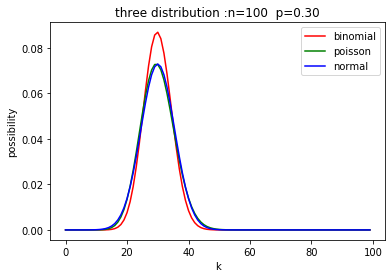
从上图中可以看出，对于固定的n以及p，当k增加时，概率P{X=k}先是随之增加直至达到最大值，随后单调减少。可以证明，一般的二项分布也具有这一性质，且: 

1. 当（n+1）p不为整数时，二项概率P{X=k}在k=[(n+1)p]时达到最大值；
2. 当（n+1）p为整数时，二项概率P{X=k}在k=(n+1)p和k=(n+1)p-1时达到最大值。

注：[x]为取整函数，即为不超过x的最大整数

 

五、二项分布与其他分布的关系

两个二项分布的和

如果X~ B(n,p)和Y~ B(m,p)，且X和Y相互独立，那么X+Y也服从二项分布；它的分布为：

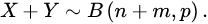
伯努利分布

伯努利分布是二项分布在n= 1时的特殊情况。X~ B(1,p)与X~ Bern(p)的意思是相同的。相反，任何二项分布B(n,p)都是n次独立伯努利试验的和，每次试验成功的概率为p

泊松近似

当试验的次数趋于无穷大，而乘积np固定时，二项分布收敛于泊松分布。因此参数为λ=np的泊松分布可以作为二项分布B(n,p)的近似，近似成立的前提要求n足够大，而p足够小，np不是很小

正态近似

如果n足够大，那么分布的偏度就比较小。在这种情况下，如果使用适当的连续性校正，那么B(n,p)的一个很好的近似是正态分布:

当n越大（至少20）且p不接近0或1时近似效果更好。不同的经验法则可以用来决定n是否足够大,以及p是否距离0或1足够远,其中一个常用的规则是np和n(1 −p)都必须大于 5

 

 回到顶部