三角函数（sin,cos,tan）、log等等

 

 

 

函数关系

 

 

 还有更多的数据具体看：https://baike.baidu.com/item/%E4%B8%89%E8%A7%92%E5%87%BD%E6%95%B0%E5%85%AC%E5%BC%8F/4374733?fr=aladdin

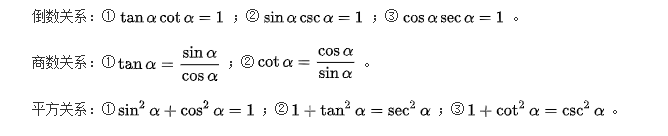
主要看看图形是怎么样的

 

#三角函数的自变量是角度
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 2 * np.pi, 50)
y = np.sin(x)
plt.plot(x, y)
plt.title('sin(x)')
plt.xticks( (0, np.pi * 0.5, np.pi, np.pi * 1.5, np.pi * 2), ('0', '2/π', 'π', '1.5π', '2π') )
plt.annotate(s='sin(2/π)=1',xy=(np.pi * 0.5,1),xytext=(0.5,0.5),color='red',arrowprops=dict(arrowstyle='-|>',connectionstyle='arc3',color='red'))
plt.annotate(s='sin(π)=1',xy=(np.pi,0),xytext=(0.5,-0.5),color='red',arrowprops=dict(arrowstyle='-|>',connectionstyle='arc3',color='red'))
plt.show()

 

 

 

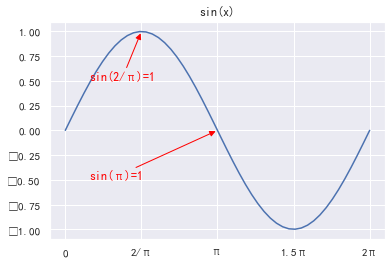
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 2 * np.pi, 50)
y = np.cos(x)
plt.plot(x, y)
plt.title('cos(x)')
plt.xticks( (0, np.pi * 0.5, np.pi, np.pi * 1.5, np.pi * 2), ('0', '2/π', 'π', '1.5π', '2π') )
plt.annotate(s='cos(2/π)=1',xy=(np.pi * 0.5,0),xytext=(0.5,0.5),color='red',arrowprops=dict(arrowstyle='-|>',connectionstyle='arc3',color='red'))
plt.annotate(s='cos(π)=1',xy=(np.pi,-1),xytext=(0.5,-0.5),color='red',arrowprops=dict(arrowstyle='-|>',connectionstyle='arc3',color='red'))
plt.show()

 

 

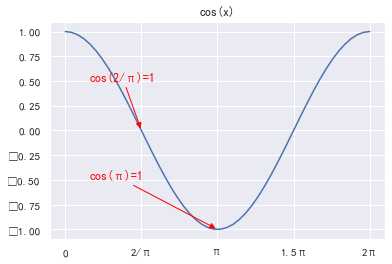
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 2 * np.pi, 50)
y = np.sin(x)/np.cos(x)
plt.plot(x, y)
plt.title('tan(x)')
plt.xticks( (0, np.pi * 0.5, np.pi, np.pi * 1.5, np.pi * 2), ('0', '2/π', 'π', '1.5π', '2π') )
plt.show()

 

 

lnx是以e为底的对数函数，其中e是一个无du限不循环小数，其值约等于2.718281828459…
函数的图象是过点（1,0）的一条C型的曲线,串过第一，第四象限，且第四象限的曲线逐渐靠近Y
轴，但不相交，第一象限的曲线逐渐的远离X轴。
其定义域：x>0 值域：y（无穷）；一般表示方法为lnx。数学中也常见以logx表示自然对数

import matplotlib.pyplot as plt
import numpy as np
x=np.arange(0.1,1000)
y=np.log(x)
plt.plot(x, y)
plt.title('lnx 或者是 logx')
plt.annotate(s='ln1=0',xy=(1,0),xytext=(0.5,0.5),color='red',arrowprops=dict(arrowstyle='-|>',connectionstyle='arc3',color='red'))
plt.show()

 

 

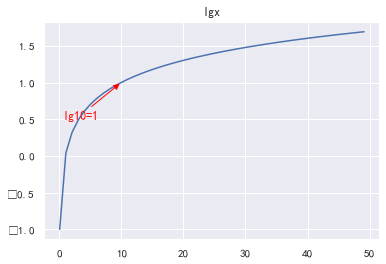
log10(x)又叫lg(x)是以10为底的对数

import matplotlib.pyplot as plt
import numpy as np
x=np.arange(0.1,50)
y=np.log10(x)
plt.plot(x, y)
plt.title('lgx')
plt.annotate(s='lg10=1',xy=(10,1),xytext=(0.5,0.5),color='red',arrowprops=dict(arrowstyle='-|>',connectionstyle='arc3',color='red'))
plt.show()