python 泰坦尼克存活问题分析
导入基本的模块
#导入模块 import numpy as np import pandas as pd from scipy import stats import seaborn as sns import matplotlib.pyplot as plt %matplotlib inline plt.rc("font",family="SimHei",size="12") #解决中文无法显示的问题
导入数据
#导入CSV数据,要不是/,要不是\\ train=pd.read_csv('F:/python/titanic_data.csv')
字段含义:
PassengerId:乘客编号
Survived:乘客是否存活
Pclass:乘客所在的船舱等级
Name:乘客姓名
Sex:乘客性别
Age:乘客年龄
SibSp:乘客的兄弟姐妹和配偶数量
Parch:乘客的父母与子女数量
Ticket:票的编号
Fare:票价
Cabin:座位号
Embarked:乘客登船码头
查查数据分布
#使用info,describe train.info() train.describe()
查看缺失值
#null train.isnull().sum()
PassengerId 0 Survived 0 Pclass 0 Name 0 Sex 0 Age 177 SibSp 0 Parch 0 Ticket 0 Fare 0 Cabin 687 Embarked 2 dtype: int64
区别类别变量和连续变量
#连续变量和类别变量分开 num_features=train.select_dtypes(include=[np.number]) categ_features=train.select_dtypes(include=[np.object]) num_features=num_features.columns categ_features=categ_features.columns
类别变量分析(['Name', 'Sex', 'Ticket', 'Cabin', 'Embarked'])主要分析性别和乘客登船码头
#类别变量的每个类别频数可视化 def count_plot(x, **kwargs): sns.countplot(x=x) x=plt.xticks(rotation=90) f = pd.melt(train, value_vars=['Sex','Embarked']) g = sns.FacetGrid(f, col="variable", col_wrap=2, sharex=False, sharey=False, size=5) g = g.map(count_plot, "value")
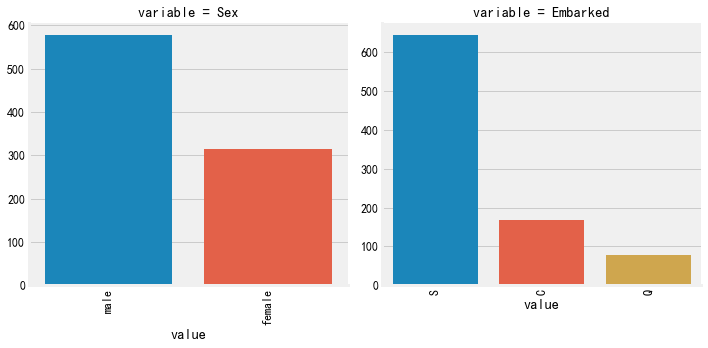
上面这种用法,在数据量较少时可以使用,数据量太大时就需要较长时间,可以看出男女比例(男占比约65%)和客户登船码头(SCQ)占比
查看这二者和存活的关系如何
#性别 fig, axes = plt.subplots(1,2,figsize=(12,6)) pd.crosstab(train["Sex"],train["Survived"]).plot(kind="bar",ax=axes[0]) a=pd.crosstab(train["Sex"],train["Survived"]) a['存活率']=a[1]/a.sum(1) a['存活率'].plot(ax=axes[1]) plt.show()
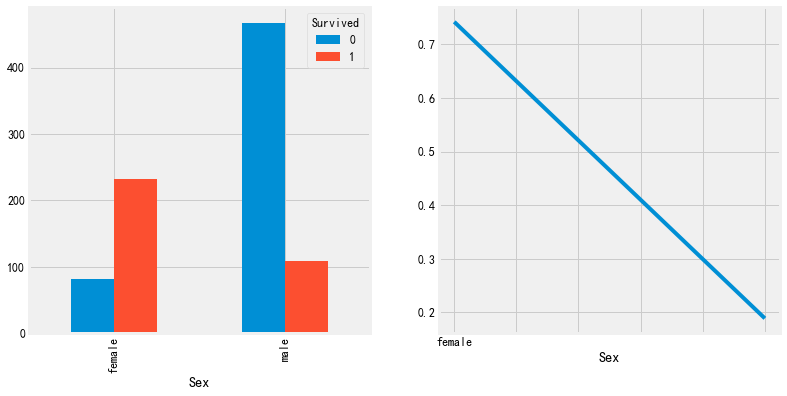
可以看出男女存活率还是有较大的影响的,女生存活率超过了70%,男生不到20%
#登船码头 fig, axes = plt.subplots(1,2,figsize=(12,6)) pd.crosstab(train["Embarked"],train["Survived"]).plot(kind="bar",ax=axes[0]) axes[0].set_title('登船码头的存活人数') a=pd.crosstab(train["Embarked"],train["Survived"]) a['存活率']=a[1]/a.sum(1) a['存活率'].plot(ax=axes[1]) axes[1].set_title('登船码头的存活率') plt.show()
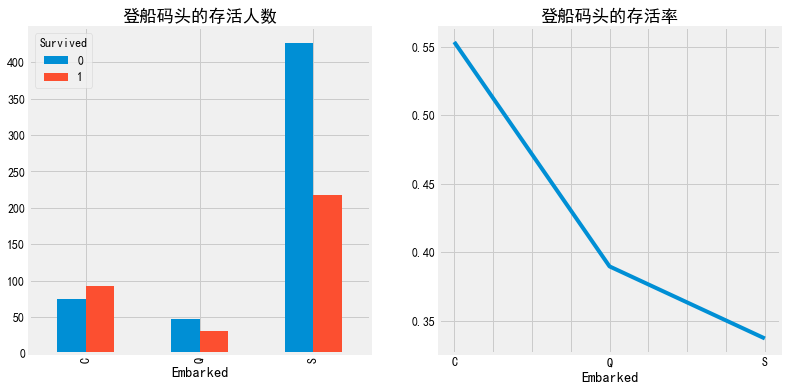
处理连续变量(['PassengerId', 'Survived', 'Pclass', 'Age', 'SibSp', 'Parch', 'Fare'])
#每个数字特征得分布可视化 f = pd.melt(train, value_vars=num_features) g = sns.FacetGrid(f, col="variable", col_wrap=2, sharex=False, sharey=False) g = g.map(sns.distplot, "value")
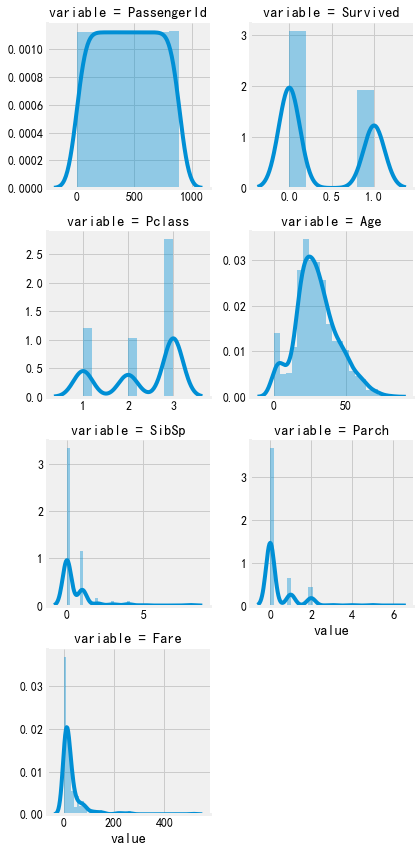
看的出只有ID和age和fare是连续性的,其他是离散型数值特征,但是ID有没有什么意义,所以只有两个是连续性特征
存活画图
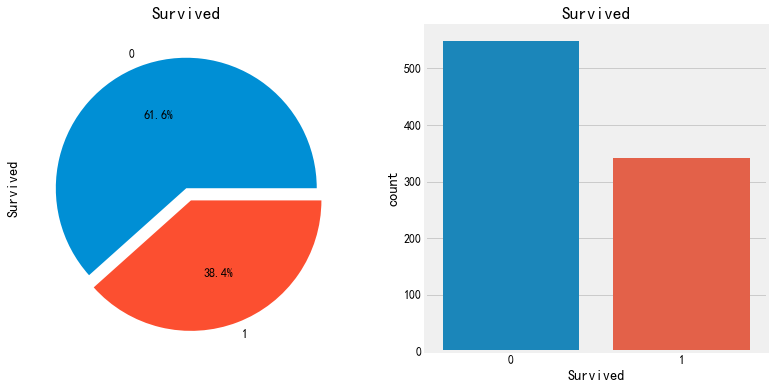
#y值画图,看看样本分布是否均衡 fig, axes = plt.subplots(1,2,figsize=(12,6)) train['Survived'].value_counts().plot.pie(explode=[0,0.1],autopct='%1.1f%%',ax=axes[0]) axes[0].set_title('Survived') #ax[0].set_ylabel('') sns.countplot('Survived',data=train,ax=axes[1]) axes[1].set_title('Survived') plt.show()
乘客所在的船舱等级
#乘客所在的船舱等级画图 fig, axes = plt.subplots(1,2,figsize=(12,6)) pd.crosstab(train["Pclass"],train["Survived"]).plot(kind="bar",ax=axes[0]) axes[0].set_title('船舱等级的存活人数') a=pd.crosstab(train["Pclass"],train["Survived"]) a['存活率']=a[1]/a.sum(1) a['存活率'].plot(ax=axes[1]) axes[1].set_title('船舱等级的存活率') plt.show()
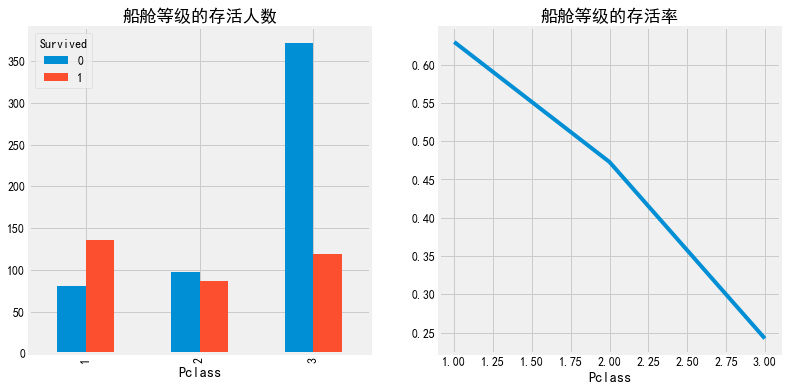
可以看出1的存活率最高,不愧是1等座
年龄处理
由于年龄是连续性数据,而且还有缺失值因此要先分箱,然后再做列联表
首先把缺失值补全
#查看缺失比例 missing=train.isnull().sum()/len(train) missing=missing[missing>0] missing.sort_values().plot.bar()
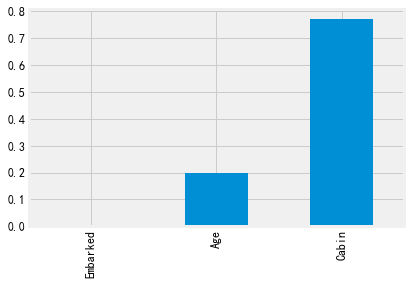
可见年龄的缺失还是很严重的(20%),由于年龄是连续性特征,我们可以使用均值进行填充
#使用均值进行填充年龄的缺失值 train['Age']=train['Age'].fillna(int(train['Age'].mean()))
构建最优分箱函数
import scipy.stats.stats as stats def mono_bin(Y, X, n = 20): ''' 构建最优分箱的函数 返回的是最优分箱的区间 ''' r = 0 good=Y.sum() #Y是标签值,也就是好坏客户,计算好用户个数 bad=Y.count()-good #坏用户个数 while np.abs(r) < 1: #np.abs(r)是求觉得值,有点疑惑,相关系数<1就一直减少分箱个数,感觉相关系数一直都是小于1 d1 = pd.DataFrame({"X": X, "Y": Y, "Bucket": pd.qcut(X, n)}) #等深分段,并且将XY和X分段好的数据组合成一个df d2 = d1.groupby('Bucket', as_index = True) #根据分箱的去分组,且不要索引 r, p = stats.spearmanr(d2.mean().X, d2.mean().Y) #斯皮尔曼等级相关系数 n = n - 1 cut=[] cut.append(float('-inf')) #负无穷 for i in range(1,n+1): qua=X.quantile(i/(n+1)) cut.append(round(qua,4)) cut.append(float('inf')) return cut
由于年龄和票价都是连续性特征,可以一起分箱,但是年龄分布不均匀,不好使用qcut,还是使用cut
fig, axes = plt.subplots(2,2,figsize=(12,12)) sns.distplot(train['Age'],ax=axes[0,0]) axes[0,0].set_title('分箱前的年龄分布') cut=[-1,5,10,18,40,55,70,100] train['age']=pd.cut(train.Age,cut) sns.countplot(train['age'],ax=axes[0,1]) axes[0,1].set_title('分箱后的年龄分布') pd.crosstab(train.age,train.Survived).plot.bar(ax=axes[1,0]) axes[1,0].set_title('分箱后的年龄存活分布') a=pd.crosstab(train.age,train.Survived) a['rate']=a[1]/(a[1]+a[0]) a['rate'].plot(ax=axes[1,1]) axes[1,1].set_title('分箱后的年龄存活率')
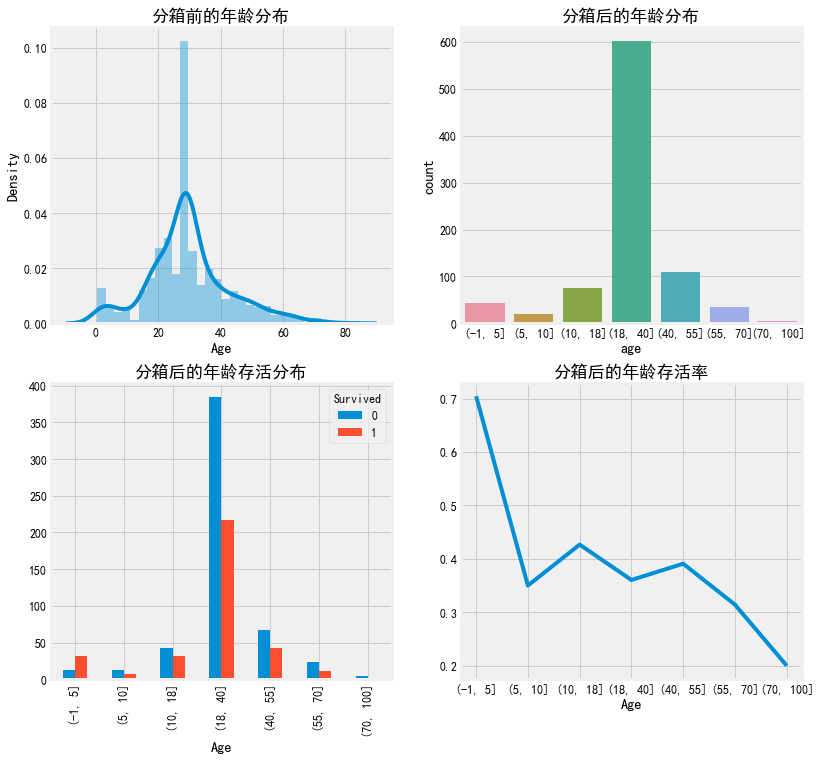
票价
#票价 fig, axes = plt.subplots(2,2,figsize=(12,12)) sns.distplot(train['Fare'],ax=axes[0,0]) axes[0,0].set_title('分箱前的票价分布') train['cut_Fare']=pd.cut(train.Fare,cut_Fare) sns.countplot(train['cut_Fare'],ax=axes[0,1]) axes[0,1].set_title('分箱后的票价分布') pd.crosstab(train.cut_Fare,train.Survived).plot.bar(ax=axes[1,0]) axes[1,0].set_title('分箱后的票价存活分布') a=pd.crosstab(train.cut_Fare,train.Survived) a['rate']=a[1]/(a[1]+a[0]) a['rate'].plot(ax=axes[1,1]) axes[1,1].set_title('分箱后的票价存活率')
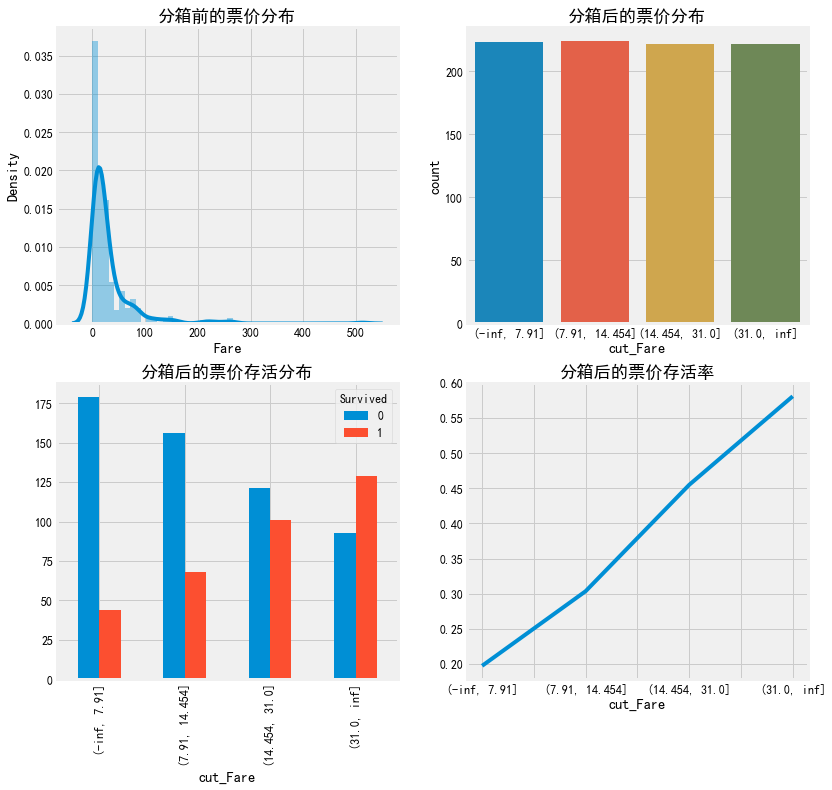
可以看出结果还是不错的
#还有这种表达 #使用箱型图查看二者分布如何 fig,ay = plt.subplots() Fare1 = train.Fare[train.Survived == 1] Fare0 = train.Fare[train.Survived == 0] plt.boxplot((Fare1,Fare0),labels=('Survived','Not Survived')) ay.set_ylim([-10,150]) ay.set_title("Boxplot of Fare")
SibSp:乘客的兄弟姐妹和配偶数量
Parch:乘客的父母与子女数量
可以分为有或者没有,毕竟有的话有抚养义务,存活下来的机会大一点
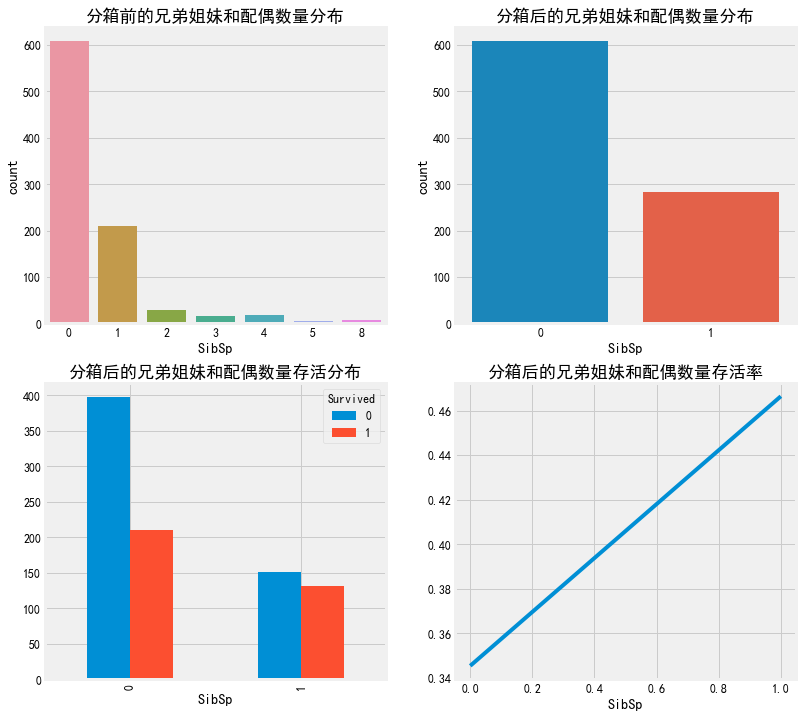
#乘客的兄弟姐妹和配偶数量 fig, axes = plt.subplots(2,2,figsize=(12,12)) sns.countplot(train['SibSp'],ax=axes[0,0]) axes[0,0].set_title('分箱前的兄弟姐妹和配偶数量分布') train['SibSp']=train['SibSp'].mask(train['SibSp']>=1,1) sns.countplot(train['SibSp'],ax=axes[0,1]) axes[0,1].set_title('分箱后的兄弟姐妹和配偶数量分布') pd.crosstab(train['SibSp'],train.Survived).plot.bar(ax=axes[1,0]) axes[1,0].set_title('分箱后的兄弟姐妹和配偶数量存活分布') a=pd.crosstab(train['SibSp'],train.Survived) a['rate']=a[1]/(a[1]+a[0]) a['rate'].plot(ax=axes[1,1]) axes[1,1].set_title('分箱后的兄弟姐妹和配偶数量存活率')
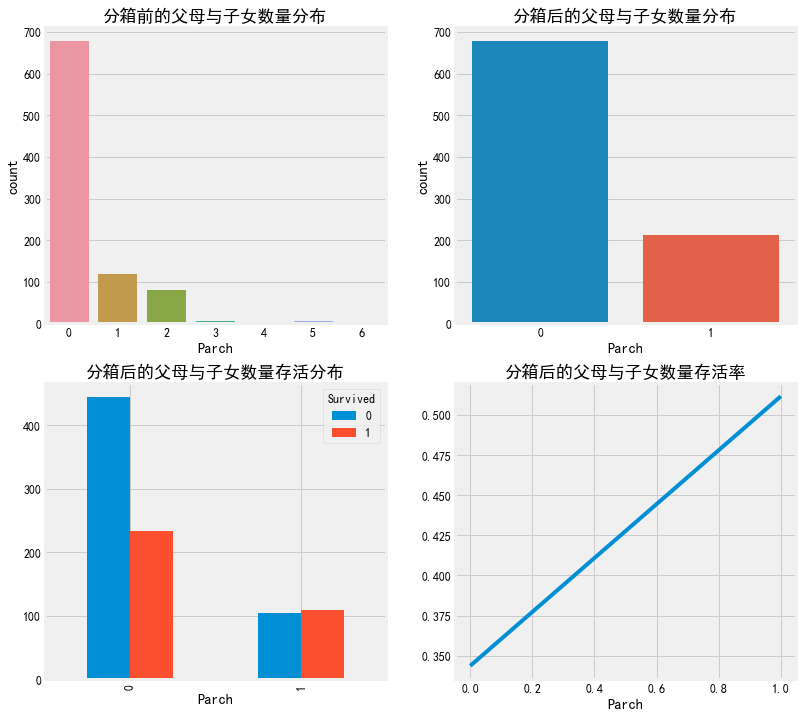
#乘客的父母与子女数量 fig, axes = plt.subplots(2,2,figsize=(12,12)) sns.countplot(train['Parch'],ax=axes[0,0]) axes[0,0].set_title('分箱前的父母与子女数量分布') train['Parch']=train['Parch'].mask(train['Parch']>=1,1) sns.countplot(train['Parch'],ax=axes[0,1]) axes[0,1].set_title('分箱后的父母与子女数量分布') pd.crosstab(train['Parch'],train.Survived).plot.bar(ax=axes[1,0]) axes[1,0].set_title('分箱后的父母与子女数量存活分布') a=pd.crosstab(train['Parch'],train.Survived) a['rate']=a[1]/(a[1]+a[0]) a['rate'].plot(ax=axes[1,1]) axes[1,1].set_title('分箱后的父母与子女数量存活率')
标签化变量
变量之间相关性分析
#corr corr=train.corr() corr["Survived"].sort_values()

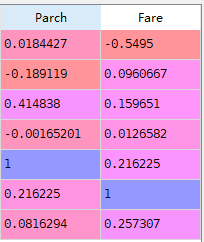

特征构造
#缺失值处理 train['Age'].mean() #29.69911764705882 train['Age'].fillna(30,inplace=True) #删除 train['Cabin'].value_counts() train=train.drop(['Cabin'],axis=1) #众数填充 train['Embarked'].value_counts() train['Embarked'].fillna('S',inplace=True) #年龄分箱 train.age=pd.cut(train.Age,[0,5,15,20,35,50,60,100]) pd.crosstab(train.age,train.Survived).plot.bar() train.Parch[(train.Parch>0) & (train.Parch<=2)]=1 train.Parch[train.Parch>2]=2 train.SibSp[(train.SibSp>0) & (train.SibSp<=2)]=1 train.SibSp[train.SibSp>2]=2 dummy_Pclass = pd.get_dummies(train.Pclass, prefix='Pclass') dummy_Sex = pd.get_dummies(train.Sex, prefix='Sex') dummy_Embarked = pd.get_dummies(train.Embarked, prefix='Embarked') dummy_Parch = pd.get_dummies(train.Parch, prefix='Parch') dummy_SibSp = pd.get_dummies(train.SibSp, prefix='SibSp') dummy_Age = pd.get_dummies(train.age, prefix='Age') train_1=dummy_Pclass.join(dummy_Sex).join(dummy_Embarked).join(dummy_Parch).join(dummy_SibSp).join(dummy_Age) train_1['Fare']=train['Fare']
模型构造
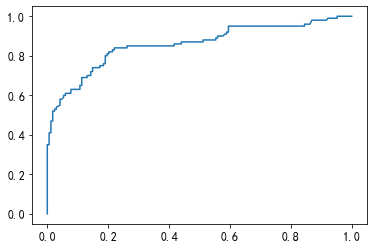
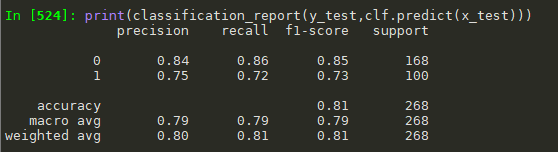
from sklearn.linear_model import LogisticRegression from sklearn.metrics import confusion_matrix, roc_curve,roc_auc_score,classification_report from sklearn.model_selection import train_test_split train_x=train_1 train_y=train['Survived'] x_train,x_test,y_train,y_test=train_test_split(train_x,train_y,test_size=0.3,random_state=0) #逻辑回归 clf = LogisticRegression() clf.fit(x_train,y_train) #用测试集进行检验 clf.predict(x_test) #混淆矩阵 confusion_matrix(y_test,clf.predict(x_test)) #array([[144, 24],[ 28, 72]], dtype=int64) #roc roc_auc_score(y_test,clf.predict_proba(x_test)[:,1]) #0.8578869047619048 #画图 fpr,tpr,thresholds = roc_curve(y_test,clf.predict_proba(x_test)[:,1]) plt.plot(fpr,tpr) #分类报告 print(classification_report(y_test,clf.predict(x_test)))



 浙公网安备 33010602011771号
浙公网安备 33010602011771号