欧拉降幂及广义欧拉降幂证明

预备知识：欧拉定理及欧拉函数求解

https://blog.csdn.net/hzj1054689699/article/details/80693756

https://www.cnblogs.com/bibibi/p/10269051.html

看完这几位大佬的博客，自己试着仔细的证明了一下，由于本人太菜，有啥证明不当的地方希望大佬们帮忙指正一下orz

欧拉降幂公式（图片来源）

 

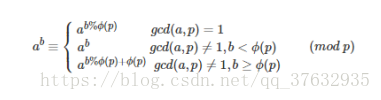
Φ(p)表示p的欧拉函数

 a ≡ b mod(p)  表示a和b在模p的情况下同余

gcd（a，b）表示a和b的最大公因数

%表示取模

1. a ^b ≡ a ^b%Φ(p)      mod(p)                ;  gcd(a,p) =1  

 由欧拉定理易证

 因为gcd(a,p) =1     ， a ^Φ(p) ≡ 1  mod(p)  

所以a ^b  ≡  a ^{b%Φ(p)+b/Φ(p)*Φ(p)}  ≡  a ^b%Φ(p)  

 

2.  a ^b ≡ a ^b  mod(p)                       ;  b< Φ(p)，gcd(a,p) ≠ 1

证明略

 

3.  a ^b ≡ a ^{b%Φ(p)+Φ(p)}   mod(p)        ;  gcd(a,p) ≠ 1

我们先证明对于任何一个a的质因子x

有x ^b ≡ x ^{b%Φ(p)+Φ(p)}   mod(p)          ;  b> Φ(p)

 

令 p=s*x^r     ( r ≥ 0)     gcd(s,x)=1;

则有 x ^Φ(s) ≡ 1  mod(s) (欧拉定理)    

又因为Φ(p)=Φ(s)*Φ(x^r)

所以x ^Φ(p) ≡ 1  mod(s)

  x ^Φ(p)  = k*s +1 (k≥0)

两边同时乘以x^r

x^Φ(p)+r = k*s*x^r+x^r

因为p=s*x^r ，所以当同时对等式两边对p取模时

x^Φ(p)+r ≡ x^r   mod(p)

因为 x ^Φ(p) ≡ 1  mod(s)

所以对于 x ^2*Φ(p) ≡ 1  mod(s)

同理可以推出x ^2*Φ(p)+r ≡ x^r   mod(p)        

综上可以推出x ^k*Φ(p)+r ≡ x^r   mod(p)   ；k≥0

 

又因为x ^b ≡ x ^b-r+r ≡ x ^b-r+Φ(p)+r ≡ x ^b+Φ(p)  mod(p)   ; b≥r，b-r≥0

Φ(p) = Φ(s)* Φ(x^r) ≥ Φ(x^r) = (x^r-1 )*(x-1) ≥ x^r-1 ≥ r

所以 x ^b ≡ x ^b+Φ(p) mod(p)    ;  *其中b≥Φ(p)

 x ^b ≡ x ^{b%Φ(p)+Φ(p)} mod(p)              ;(x ^{b%Φ(p)+Φ(p)} ≡x ^{b%Φ(p)+2*Φ(p)} ≡...≡x ^{b%Φ(p)+k*Φ(p)} ≡x ^b   mod(p))    (  b = b%Φ(p) + k*Φ(p) )

 

我们为什么用 x ^b ≡ x^{b%Φ(p)+Φ(p)} mod(p)    而不用 x ^b ≡ x^b%Φ(p) mod(p)    呢

这是因为我们推出 x ^b ≡ x^b+Φ(p) mod(p) 这个式子的前提是 b ≥ Φ(b) ，如果用b%Φ(p)去推，我们推不出x ^b%Φ(p) ≡ x^b mod(p)

 

现在我们已经推出了x ^b ≡ x^{b%Φ(p)+Φ(p)} mod(p)    ，其中x是a的质因子，p是模

 

对于质数的幂也可以推出一样的结果

(x^k) ^b = x ^{k* b} ≡ x^Φ(p)+k*b ≡ x ^k*(p)+k*b ≡ (x^k) ^Φ(p)+b ≡ (x^k) ^{b%Φ(p)+Φ(p)}  mod(p) ;b≥Φ(p) , k >0

 

然后我们将a分解质因子成a=∏x_i ^k_i ,对于每一个x我们都满足上面的x ^b ≡ x^{b%Φ(p)+Φ(p)} mod(p)

我们将他们乘起来就是a ^b ≡ a^{b%Φ(p)+Φ(p)} mod(p)

证毕