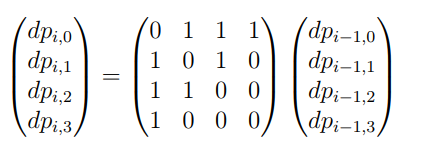牛客小白月赛7

链接：https://www.nowcoder.com/acm/contest/190/A
来源：牛客网

A.

做水题就是在浪费时间，但是一场比赛要是没有送分的签到题，大家的比赛体验就会很差。为了优化你的比赛体验又不浪费你的读题时间，我并不打算给你很复杂的故事背景，你只需要复制下面的代码并选择正确的语言提交即可通过此题。

#include<iostream>
using namespace std;
long long f(long long n)
{
    if (n < 20180001) return n + 2017;
    return f(f(n - 2018));
}
int main()
{
    long long n;
    cin >> n;
    cout << f(n) << endl;
    return 0;
}

输入描述:

输入一个整数n。(1 ≤ n ≤ 10

¹⁸

输出描述:

输出一个整数表示答案。

输入

20182017

输出

20182017
分析: 蛮有意思的签到题.  直接交,肯定是可以A的. 不行看:

 , 很真实的通过率.
     我们稳妥点分析,(把代码复制到本地,随便输入几个数...)然后我们发现, n小于20180001时输出n+2017  否则输出20182017 就OK了.

#include<iostream>
using namespace std;
int main()
{
    long long n;
    cin >> n;
    if (n < 20180001) cout << 2017 + n << endl;
    else cout << 20182017 << endl;
    return 0;
}

View Code

链接：https://www.nowcoder.com/acm/contest/190/B
来源：牛客网

B.题目描述

Alice和Bob产生了不可调节的矛盾，于是他们相约一起玩一个自杀游戏，输的人就会从这个世界上消失。

游戏开始时，Alice手上拿着一个定时炸弹，炸弹有个倒计时t。炸弹在t=0时刻会爆炸，此时手上拿着炸弹的人会从这个世界上消失。为了增加游戏乐趣，他们约定每个人拿到炸弹后可以选择将炸弹的时间调快d秒(d ∈ [a,b])，或者不调。每次交换炸弹会消耗1秒（假设调节炸弹时间不需要消耗时间）。

问题来了，如果双方都足够聪明，谁会活下去呢？

输入描述:

第一行有三个整数t,a,b，分别表示炸弹初始时刻的倒计时，可调节时间的范围。(0 ≤ t ≤ 10^5,1 ≤ a ≤ b ≤ 10)

输出描述:

若Alice存活则输出"Alice"，若Bob存活则输出"Bob"。

输入

6 3 4

输出

Alice

说明

Alice只需要将炸弹调快3秒后再给Bob，Bob就会拿到一个2秒后爆炸的炸弹。

分析: 看到t的范围不是很大,

所以我们可以假定一个状态state[t]表示炸弹时间为t的存活状态,

state[t]==1表示Alice在t时刻存活,Bob死亡,

state[t]==0表示在t时刻Alice死亡, Bob存活.

然后每次可以调控[a,b]的时间,同时传递炸弹需要1秒,

所以,我们的状态可以这样转移:

当state[t-(b+1)]...state[t-(a+1)]存在一个state[x]==0时 state[t] = 1

或者当 state[t-1]==0时 state[t] = 1

可以理解为: 如果时间为炸弹[t-1]或者[t-(b+1)]~[t-(a+1)]的游戏的结果都是最优解了,而现在炸弹的时间增加了,所以如果在过去的一段区间出现Alice死亡的结局,那么现在就可以翻转这个结局了.

#include <cstdio>

using namespace std;

const int maxn = 1e5+500;

bool living[maxn]; // living[t]==true表示t时刻Alice活,Bob死 

int main() {
    int i, j, t, a, b;
    scanf("%d%d%d", &t, &a, &b);
    for (i=1; i<=t; ++i) {
        if (!living[i-1]) living[i] = true; // 表明上一次游戏的最优解Alice死,Bob活,状态转移,当前游戏的Alice活,Bod死 
        for (j=i-b-1; j<=i-a-1; ++j) {      // 因为传递炸弹要用1秒 所以还要减一 
            if (j>=0 && !living[j]) {       // 表明上一次游戏的最优解有Alice死,Bob活,状态转移,当前游戏的Alice活,Bod死 
                living[i] = true;
                break;
            }
        }
    }
    printf("%s\n", living[t] ? "Alice" : "Bob" );
    
    return 0;
}

View Code

链接：https://www.nowcoder.com/acm/contest/190/C
来源：牛客网

C.题目描述

有一天，MWH突然来了兴致，想和CSL比比谁枪法好。于是他们找来了一个瓶子，比比看谁先打中这个瓶子。给定MWH的命中率 $\alpha\%$ 和CSL的命中率 $\beta\%$ 。两人轮流射击，MWH先手，问谁获胜的概率大？

输入描述:

输入两个整数

$\alpha$

和

$\beta$

，表示MWH和CSL的命中率。

$(0 \leq \alpha,\beta \leq 100)$

输出描述:

若MWH获胜的概率大，则输出"MWH"。 若CSL获胜的概率大，则输出"CSL"，否则输出"equal"。

输入

100 100

输出

MWH

输入

0 100

输出

CSL
分析: 很明显的一道数学题. 所以推公式. 是不可能的.  我暴力计算不知道什么东西...然后就过了....(应该是期望吧...大概..反正很玄学的过了...)

#include <cstdio>
#include <cmath>
int main() {
    double a, b;
    scanf("%lf%lf", &a, &b);
    a /= 100.0; b /= 100.0;
    double win1 = a, win2 = (1 - win1) * b;
    for (int i=1; i<=10000000; ++i) {
        win1 = win1 + a * (1 - win2);
        win2 = win2 + b * (1 - win1);
    }
    double eps = 1e-7;
    if (fabs(win1 - win2) <= eps) printf("equal\n");
    else if (win1 > win2) printf("MWH\n");
    else printf("CSL");
    return 0;
}

View Code

链接：https://www.nowcoder.com/acm/contest/190/D
来源：牛客网

D.题目描述

今天是个特殊的日子，CSL和他的小伙伴们围坐在一张桌子上玩起了明七暗七的游戏。游戏规则是这样的：

一个人报出一个起始数，接下来按照逆时针的顺序轮流报数，如果碰到数是7的倍数或含有7，则拍手，下一个人接着报数。直到有一个人报错了数字或者没有及时拍手为止。

玩游戏嘛，当然得有惩罚。这么简单的游戏对CSL的学霸小伙伴而言实在是太无脑了，轻轻松松数到上万根本不在话下。但是对于数学是体育老师教的CSL来说，实在是太难了。快帮他算算什么时候应该拍手吧。

输入描述:

输入两个整数m和n。(1 ≤ m, n ≤ 10^12)

输出描述:

输出一个整数，表示m以后第n个需要拍手的数字。

输入

30 7

输出

输入

56 1

输出

57

分析: 我们记[1..n]中含有7的或者可以被7整除的数字个数为a. 而我们要求得就是第m+a个含有7的或者可以被7整除的数字. 
     对于这种问题,我们应该很容易想到数位dp, 
     然后数位dp我们可以求   [1..n]中不含有7的且不可以被7整除的数字个数.
     所以  [1..n]中含有7的或者可以被7整除的数字个数  = n - [1..n]中不含有7的且不可以被7整除的数字个数.
     所以,我们求出  [1..n]中含有7的或者可以被7整除的数字个数  后,我们就可以二分我们的答案来求出数字了.

#include <cstdio>
#include <cstring>

using namespace std;

typedef long long ll;

ll dp[20][8];
int digit[25];

ll dfs(int deep, ll state, bool lmt) {
    if (!deep) return state ? 1 : 0;
    if (!lmt && dp[deep][state]>=0) return dp[deep][state];
    int i, up = lmt ? digit[deep] : 9;
    ll cnt = 0;
    for (i=0; i<=up; ++i) {
        if (i==7) continue;
        cnt += dfs(deep-1, (state*10+i)%7, lmt && i==up);
    }
    return lmt ? cnt : dp[deep][state]=cnt;
}

ll cal(ll num) {
    int k = 1;
    while (num) {
        digit[k++] = num % 10;
        num /= 10;
    }
    return dfs(k-1, 0, true);
}

int main()
{
    ll n, m, left, right, mid, tmp;
    
//    printf("%d %d\n", 14-cal(14*1ll), cal(14));
    while (~scanf("%lld%lld", &m, &n)) {
        memset(dp, -1, sizeof(dp));
        left = 0; right = 1LL*1e18;
        tmp = m - cal(m); // 
        while (left <= right) {
            mid = (left + right) / 2;
            if (mid-cal(mid) >= tmp+n) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        printf("%lld\n", left);
    }
    
    return 0;
}

View Code

链接：https://www.nowcoder.com/acm/contest/190/E
来源：牛客网

E.题目描述

Applese有个神奇的能力，TA可以把m个硬币融合成1个硬币，是不是很厉害。现在Applese有n个硬币，TA想把这个n个硬币融合成1个，请问他能完成吗?

输入描述:

输入两个整数n,m(1 ≤ n, m ≤ 10^9)

输出描述:

如果Applese能完成,输出"Yes"，否则输出"No"。

输入

10 7

输出

No
分析: 我们发现...这是一道模拟题. 然后要注意死循环. 然后没了.

#include<iostream>
using namespace std;
int main()
{
    long long n, m;
    cin >> n >> m;
    long long lst = n;
    while (n && n!=1) {
        n = n / m + n % m;
        if (n == lst) break;
        lst = n;
    }
    if (n == 1) cout << "Yes" << endl;
    else cout << "No" << endl;
    return 0;
}

View Code

链接：https://www.nowcoder.com/acm/contest/190/F
来源：牛客网

F.题目描述

Bob在学习了DFS后，自己又发明了一种新的搜(luan)索(gao)方法，叫做BFS(Bobby First Search)。

这种搜索被定义为：在一个字符串中，从前向后查找第一个子串"Bob"出现的位置。（不区分大小写）

输入描述:

输入一个不含空格的字符串S（可能含有大小写字母，数字）。(1 ≤ |S| ≤ 100)

输出描述:

输出一个数字，表示"Bob"第一次出现的位置（下标从0开始）。

如果没有出现，则输出"-1"。

输入

Bobob

输出

输入

bobby

输出

输入

BFS

输出

-1
分析: 没啥好讲的.

#include <cstdio>
#include <cstring>
#include <cctype>
char str[128];
int main()
{
    scanf("%s", str);
    for (int i=0; str[i]; ++i) str[i] = tolower(str[i]);
    int idx = strstr(str, "bob") - str;
    printf("%d\n", idx < 0 ? -1 : idx);
    return 0;
}

View Code

链接：https://www.nowcoder.com/acm/contest/190/G
来源：牛客网

G.题目描述

CSL手上有n个苹果，第i个苹果的质量是w_i，现在他想把这些苹果分给他的好朋友wavator和tokitsukaze。但是CSL为了不让他们打架，根据质量决定尽量地均分成两堆分给他们。现在CSL想知道到底给每个人分多少质量的苹果。

注意：苹果不能劈开来，并且如果不能正好均分，tokitsukaze小姐姐会拿到重的那一堆。

输入描述:

第一行输入一个整数n(2 ≤ n ≤ 100)，第二行n个整数，表示每个苹果的质量wi(1 ≤ wi≤ 100)。

输出描述:

输出两个整数，分别表示wavator和tokitsukaze得到的苹果的质量。

输入

3
2 2 2

输出

2 4
分析: 这是一道比较经典的01背包问题.  
     思路是,把总质量除以二作为最大容量,每一个苹果的花费和收益都是它的重量,然后就是一个裸的01背包.  
     为什么这样可以呢? 
     因为,它要两个人的质量差尽量小,同时苹果不能分割,所以把总质量的一半作为01背包的最大容量,然后尽可能的取最大质量.
     然后答案很明显就是我们要的.
     (我才不会承认,,,,我写不来01背包了...直接copy以前的01背包答案就扔上去了....
     而且还是没有优化的01背包...代码有点丑..最后感谢出题人不杀)

#include <cstdio>
#include <algorithm>
 
using namespace std;
 
const int maxn = 128;
int date[128];
 
int dp[124][10024];
 
int main()
{
    int n, i, j, sum = 0;
    scanf("%d", &n);
    for (i=1; i<=n; ++i) {
        scanf("%d", date+i);
        sum += date[i];
    }
    int tmp = sum;
    sum /= 2;
    for (i=1; i<=n; ++i) {
        for (j=1; j<=sum; ++j) {
            if (j>=date[i]) dp[i][j] = max(dp[i-1][j], dp[i-1][j-date[i]] + date[i]);
            else            dp[i][j] =  dp[i-1][j];
        }
    }
    printf("%d %d\n", min(tmp - dp[n][sum], dp[n][sum]), max(tmp - dp[n][sum], dp[n][sum]));
     
    return 0;
}

View Code

链接：https://www.nowcoder.com/acm/contest/190/H
来源：牛客网

H.题目描述

今天是阳光明媚，晴空万里的一天，CSL早早就高兴地起床走出寝室到校园里转悠。

但是，等到他回来的时候，发现他的校园卡不见了，于是他需要走遍校园寻找它的校园卡。CSL想要尽快地找回他掉的校园卡，于是便求助于OneDay帮他一起找。

OneDay和CSL在同一已知的地点出发，并以相同的速度（1格/秒）搜索校园，试求两人走遍校园的最短时间。

输入描述:

第一行为两个整数n,m(1 ≤ n, m ≤ 4)，表示地图的大小。接下来是n行m列的地图：X表示障碍物，S表示起点，O表示空地。障碍物不能直接经过，数据保证所有空地是可达的，起点有且只有一个。

输出描述:

输出一个整数表示两人共同走遍校园所需的最少时间。

输入

3 4
XSOO
OOXO
OOOO

输出

说明

输入

2 3
XSX
OOO

输出

输入

4 4
SOOO
OOOO
OOOO
OOOO

输出

分析: 很明显的bfs....之前做了一个搜索入门的题..写了半个多少小时..发现自己写的不知道什么东西....
     然后自闭了.. 看的题解写的.   
     我们发现n,m只有[1,4], 所以对于地图的记录,我们可以状态压缩,直接通过一个数来表示.
     然后我们可以开一个 vis[1<<16][4][4][4][4] 数组来记录  vis[地图][x1][y1][x2][y2]
     如果写过一些搜索题,应该就很简单了.

#include <cstdio>
#include <queue>
 
using namespace std;
 
bool vis[1<<16][4][4][4][4];
int n, m;
char _m[5][5];
 
struct nobe {
    int val;
    int x1;
    int y1;
    int x2;
    int y2;
    int step;
    nobe () { };
    nobe (int xx1, int yy1, int xx2, int yy2, int vv, int ss) : x1(xx1), y1(yy1), x2(xx2), y2(yy2), val(vv), step(ss) { }
};
 
inline int get(int x1, int y1, int x2, int y2, int val) {
    val |= (1 << ((x1 * m) + y1));
    
    val |= (1 << ((x2 * m) + y2));
    return val;
}
 
int dir[] = {1, 0, -1, 0, 1};
 
int bfs(nobe st) {
    queue<nobe> q;
    nobe now;
    int x1, y1, x2, y2, step, val, tmp;
    int ed = 0, i, j;
    for (i=0; i<n; ++i) {
        for (j=0; j<m; ++j) {
            ed |= (1 << (i * m + j));
        }
    }
    q.push(st);
    while (!q.empty()) {
        now = q.front(); q.pop();
        x1 = now.x1; y1 = now.y1; x2 = now.x2; y2 = now.y2; step = now.step; val = now.val;
        if (x1<0 || x1>=n || y1<0 || y1>=m) continue;
        if (x2<0 || x2>=n || y2<0 || y2>=m) continue;
        if (_m[x1][y1]=='X') continue;
        if (_m[x2][y2]=='X') continue;
        if (val == ed) return step;
        if (vis[val][x1][y1][x2][y2]) continue;
        vis[val][x1][y1][x2][y2] = true;
         
        for (i=1; i<5; ++i) {
            for (j=1; j<5; ++j) {
                tmp = get(x1+dir[i-1], y1+dir[i], x2+dir[j-1], y2+dir[j], val);
                q.push(nobe(x1+dir[i-1], y1+dir[i], x2+dir[j-1], y2+dir[j], tmp, step+1));
            }
        }
    }
    return -1;
}
 
int main()
{
//  freopen("E:\\input.txt", "r", stdin);
    int i, j;
    scanf("%d%d", &n, &m);
    int val, x, y;
    val = 0;
    for (i=0; i<n; ++i) {
        scanf("%s", _m[i]);
        for (j=0; j<m; ++j) {
            if (_m[i][j] == 'X' || _m[i][j] == 'S')
                val |= (1 << (i * m + j));
            if (_m[i][j] == 'S') {
                x = i;
                y = j;
            }
        }
    }
    printf("%d\n", bfs(nobe(x, y, x, y, val, 0)));
         
    return 0;
}

View Code

链接：https://www.nowcoder.com/acm/contest/190/I
来源：牛客网

I.题目描述

CSL正在学习《计算机办公自动化》文件的建立与删除。

CSL发现，当他新建一个word文档时，会得到一个名为"新建 Microsoft Office Word 文档.doc"的文件，再新建一个，则名为"新建 Microsoft Office Word 文档(2).doc"，再新建，便是"新建 Microsoft Office Word 文档(3).doc"。不断新建，编号不断递增。倘若他已经新建了三个文档，然后删除了"新建 Microsoft Office Word 文档(2).doc"，再新建一个就又会得到一个"新建 Microsoft Office Word 文档(2).doc"。

严格来说，Windows在每次新建文档时，都会选取一个与已有文件编号不重复的最小正整数作为新文档的编号。

现在，请你编程模拟以上过程，支持以下两种操作：

New：新建一个word文档，反馈新建的文档的编号；

Delete id：删除一个编号为id的word文档，反馈删除是否成功。

初始时一个文件都没有，"新建 Microsoft Office Word 文档.doc"的编号算作1。

输入描述:

第一行一个正整数n表示操作次数，接下来n行，每行表示一个操作。若该行为"New"，则表示新建，为:Delete id"则表示要删除编号为id的文档，其中id为一个正整数。操作按输入顺序依次进行。操作次数不超过100000，删除编号的数值不超过100000。

输出描述:

对于输入的每一个操作，输出其反馈结果。对于新建操作，输出新建的文档的编号；对于删除操作，反馈删除是否成功：如果删除的文件存在，则删除成功，输出"Successful"，否则输出"Failed"。

输入

12
New
New
New
Delete 2
New
Delete 4
Delete 3
Delete 1
New
New
New
Delete 4

输出

1
2
3
Successful
2
Failed
Successful
Successful
1
3
4
Successful

分析: 我们可以把题意翻译成:
     我们开始有一个集合[1...n], 
     然后有2个操作, 
     1. New 输出集合中的最小数,同时删除这个最小数.
     2. Delete num 查找集合中是否有这个数,如果有输出Failed,否则输出Successful,同把num插入到集合.
     一个Set模拟的题.

#include <set>
#include <cstdio>
#include <cstring>

using namespace std;

char op[32];

int main()
{
    int t, i, id;
//    freopen("E:\\input.txt", "r", stdin);
    scanf("%d", &t);
    set<int> se;
    for (i=1; i<=100500; ++i) se.insert(i);
    while (t--) {
        scanf("%s", op);    
        if (op[0] == 'N') {
            printf("%d\n", *se.begin());
            se.erase(se.begin());
        } else {
            scanf("%d", &id);
            if (se.find(id) != se.end()) printf("Failed\n");
            else printf("Successful\n"),  se.insert(id);
        }
    } 
    
    
    return 0;
}

View Code

链接：https://www.nowcoder.com/acm/contest/190/J
来源：牛客网

题目描述

给一个m x n的方格，Applese想要给方格填上颜色，每个格子可以是黑色或者白色。他要求左右相邻两格不能同为白色且相邻两列不能全为黑色。

求满足条件的方案数。

输入描述:

输入两个整数m, n。(1 ≤ m ≤ 5, 1 ≤ n ≤ 10^18)。

输出描述:

1e9+7取模。

输入

3 1

输出

输入

3 5

输出

输入

5 5

输出

分析: 这道题我也是看题解和别人博客才明白的.  然后我觉得做法特别妙..如果没有做过这种题,我觉得想不到.
     我们发现题目中的限制:  左右不能有相邻的白色, 两列不能全为黑色. 都只与列有关,与行无关. 同时每一列都只有2^m中排列,m特别小.
     所以我们可以用二进制来表示这一列的状态, 我们白色用1来表示, 黑色用0表示. 
     例如当m=4时有一列: 白 黑 白 白 的排序, 就是 1011 ,这个我们用一个十进制数11来表示 
     然后如果一个状态k可以由另一个状态a转移过来 那么就需要满足 (a&k)==0 && (a | k) (左右不能有相邻的白色, 两列不能全为黑色)
     例如 1011 可以由 0100 或者 0000 等转过来
     然后我们可以定义f[第i列][当前状态a]来表示转移到第i列状态a的方案数. 
     f[第i列][当前状态] = sigma(f[第i-1列][可以转移到当前状态的状态]). n特别大,我们用矩阵快速幂来做.
     我就粘个题解的图,当2*n时的矩阵

#include <cstdio>
#include <iostream>

using namespace std;

typedef long long ll;

const ll mod = 1e9+7;

class Matrix {
public:
    int r, c;
    ll mat[32][32];
    
    ll *operator [] (int x) { return mat[x]; }
    
    Matrix operator * (const Matrix &a) const {
        Matrix res;
        res.r = r; res.c = a.c;
        int i, j, k;
        for (i=0; i<res.r; ++i) {
            for (j=0; j<res.c; ++j) {
                res[i][j] = 0;
                for (k=0; k<c; ++k) 
                    res[i][j] = (res[i][j] + mat[i][k] * a.mat[k][j] % mod) % mod;
            }
        }
        return res;
    }
}mat, mat2;

Matrix pwr(const Matrix &a, ll k) {
    Matrix base = a, r;
    int i, j;
    r.r = a.r; r.c = a.c;
    for (i=0; i<r.r; ++i)
        for (j=0; j<r.c; ++j)
            r[i][j] = i==j;
    while (k) {
        if (k & 1) r = r * base;
        base = base * base;
        k >>= 1;
    }
    return r;
}

int main()
{
    int i, j;
    ll n, m;
    cin >> m >> n;
    mat.c = mat.r = (1 << m);
    mat2.c = 1; mat2.r = (1 << m); 
    for (i=0; i<(1<<m); ++i) {
        mat2[i][0] = 1;
        for (j=0; j<(1<<m); ++j) {
            mat[i][j] = 1ll * (((i & j) == 0) && (i | j));
        }        
    }

    mat = pwr(mat, n-1);
    mat = mat * mat2;
    ll res = 0;
    for (i=0; i<(1<<m); ++i) {
        res = (res + mat[i][0]) % mod;
    }
    cout << res << endl;
}

View Code

posted @ 2018-09-16 22:08 过路人1998 阅读(1006) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

过路人1998

牛客小白月赛7

A.

输入描述:

输出描述:

输入

输出

B.题目描述

输入描述:

输出描述:

输入

输出

说明

C.题目描述

输入描述:

输出描述:

输入

输出

输入

输出

D.题目描述

输入描述:

输出描述:

输入

输出

输入

输出

E.题目描述

输入描述:

输出描述:

输入

输出

F.题目描述

输入描述:

输出描述:

输入

输出

输入

输出

输入

输出

G.题目描述

输入描述:

输出描述:

输入

输出

H.题目描述

输入描述:

输出描述:

输入

输出

说明

输入

输出

输入

输出

I.题目描述

输入描述:

输出描述:

输入

输出

题目描述

输入描述:

输出描述:

输入

输出

输入

输出

输入

输出

公告