南京网络赛

A题  An Olympian Math Problem:

求S(n) = 1*1! + 2*2! + 3*3! + 4*4! + ... + (n-1)*(n-1)!

链接: https://nanti.jisuanke.com/t/30990

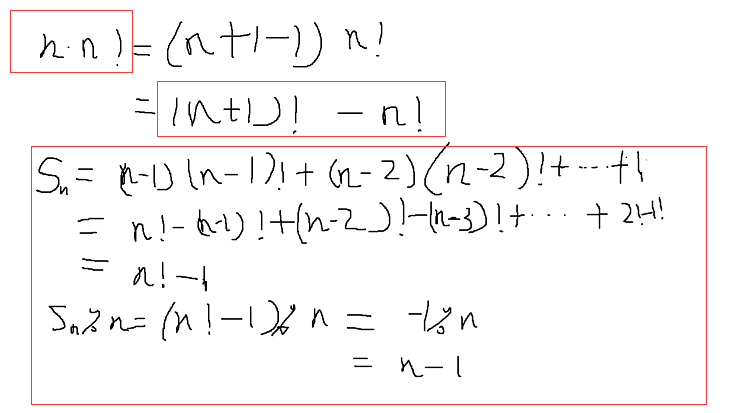
所以直接输出n-1完事

#include <bits/stdc++.h>

using namespace std;

long long n;

int main()
{
    int t;
    scanf("%d", &t);
    while (t--) {
        scanf("%lld", &n);
        printf("%lld\n", n-1);
    }
    return 0;
}

 

C. GDY 

链接: https://nanti.jisuanke.com/t/30992

模拟题: 

题意就是  n个人打牌, 然后有m张牌的栈,每个人最开始依次从栈取5张牌, 栈保证初始时,每个人至少有一张牌.

                规则1 : 牌除了一种例外外, 必须安装 3 --> 4 --> 5 --> 6 --> 7 --> 8 --> 9 --> 10 --> 11 --> 12 --> 13 --> 1 --> 2 的顺序打出

                规则3 : 例外就是, 如果不能按照顺序,但是前面打出的牌小于2,同时你有2,你可以打出2.

                规则2 : 你如果同时有2和下一张牌, 你会优先打出下一张牌.

                规则4 : 如果可以打出牌,那么一定会出牌.

                规则5 : 如果没有人能出牌,那么从最后一个出牌的人开始,每个人都抽一张牌.然后从最后一个出牌的人继续出牌.  

                规则6 : 第一个出牌的人,出的是他牌面里最小的牌.

                规则7 : 如果栈没有牌了,而且有人不能出牌了,则忽略这个人.

                规则8 : 如果有人牌打完了,那么这人就是赢家,其他人的得分就是他们手上剩下的牌的总和.

好的 按时规则模拟.

因为有次序,同时我们可以处理一下,把1变成14 2变成15,然后用一个multiset来存会方便很多.

然后我们注意到,对于当前出牌人来说,如果他出的牌有n-1个人不能出牌,那么就从他开始抽牌.

所以我们可以定义一个cnt计数器,表示多少个人不能出牌.  

#include <set>
#include <cstdio>

using namespace std;

multiset<int> se[256];
int st[25600];
int top;

int main()
{
    int t, n, m, i, j, pos, now, old, cnt;
    multiset<int>::iterator it1, it2;
    scanf("%d", &t);
    for (int cas=1; cas<=t; cas++) {
        scanf("%d%d", &n, &m);
        for (i=1; i<=n; ++i) se[i].clear();
        for (i=m; i; --i) {
            scanf("%d", st+i);
            if (st[i] <= 2) st[i] += 13;
        }
                        
        top = m;
        for (i=1; i<=n; ++i) 
            for (j=1; j<=5 && top; ++j) 
                se[i].insert(st[top--]);
        old = *se[1].begin() - 1;
        now = 1;
        bool isgameover = false;
        while (!isgameover) {
            cnt = 0;
            while (1) {    
                if (now > n) now = 1;
                if (cnt == n-1) break; // 因为经过n-1次 now也回到了出牌人,所以直接break 
                it1 = se[now].end(); it1--;
                it2 = se[now].find(old+1);
                if (old==15) {
                    now--;
                    break;
                }
                if (it2 != se[now].end()) {
                    old = *it2;
                    se[now].erase(it2);
                    if (se[now].empty()) {
                        isgameover = true;
                        break;
                    }
                    now++;
                    cnt = 0;
                } else if (*it1 == 15) {
                    old = 15;
                    se[now].erase(it1);
                    if (se[now].empty()) {
                        isgameover = true;
                        break;
                    }
                    break;  // 以后后面可能没人可以再出牌了 所以直接break. 当然 把 break 改写成 now++; cnt=0; 也是等价的. 
                } else cnt++, now++;
            }
            if (isgameover) break;
            if (now < 1) now = n;
            for (pos=now, i=1; i<=n && top; ++i, ++pos) {
                if (pos > n) pos = 1;
                se[pos].insert(st[top--]);
            }
            old = *se[now].begin();
            se[now].erase(se[now].begin());
            if (se[now].empty()) {
                isgameover = true;
                break;
            }
            now++;
        }
        printf("Case #%d:\n", cas);
        for (i=1; i<=n; ++i) {
            if (se[i].empty()) printf("Winner\n");
            else {
                int res = 0;
                for (int it : se[i]) {
                    res += it<=13 ? it : it-13;
                }
                printf("%d\n", res);
            }
        }
    }
    
    return 0;
}

 

 

L. Magical Girl Haze: 

链接: https://nanti.jisuanke.com/t/31001

给你一副有向图,从1出发,可以最多可以让k条路径为0,求到n的最短路径 (K<=10) 

我们发现K特别小.

所以考虑一下Dij, 然后我们把路变为0和不修改路都添加进去, 直接跑就OK了

#include <cstdio>
#include <queue>
#include <cstring>
#include <algorithm>
#include <iostream>

using namespace std;

typedef long long ll;

const int maxn = 100500;

struct Edge {
    int lst;
    int to;
    ll val;
}edge[maxn*2];
int head[maxn];
int qsz;

int qn, qk;

inline void add(int u, int v, ll val) {
    edge[qsz].lst = head[u];
    edge[qsz].to  = v;
    edge[qsz].val = val;
    head[u] = qsz++;
}


struct nobe {
    int to;
    int k;
    ll  w;
    nobe () { }
    nobe (int tt, int kk, ll ww) : to(tt), k(kk), w(ww) { }
    bool operator < (const nobe &a) const {
        return w > a.w;
    }
};

bool vis[11][maxn];
ll  dist[11][maxn];

ll Dij(int ed) {
    //cout << ed << endl;
    priority_queue<nobe> pq;
    nobe now;
    int i, u, k, v, j;
    ll w;
    
    for (i=1; i<=qn; ++i) {
        for (j=0; j<=qk; ++j) {
            dist[j][i] = 862621363;
             vis[j][i] = false;
        }
    }
    
    dist[0][1] = 0;
    pq.push(nobe(1, 0, 0));
    while (!pq.empty()) {
        now = pq.top(); pq.pop();
        u = now.to; k = now.k; w = now.w;
        if (vis[k][u]) continue;
        vis[k][u] = true;
        for (i=head[u]; i; i=edge[i].lst) {
            v = edge[i].to;
            if (k<qk && dist[k+1][v] > w) {
                dist[k+1][v] = w;
                pq.push(nobe(v, k+1, w));
            }
            if (dist[k][v] > w + edge[i].val) {
                dist[k][v] = w + edge[i].val;
                pq.push(nobe(v, k, dist[k][v]));
            }
        }
    }
    
    ll res = 0x3fffffffffffffff;
    for (i=0; i<=qk; ++i) 
        res = min(res, dist[i][ed]);
    return res;
}

int main()
{
//    freopen("E:\\input.txt", "r", stdin);
    int t, n, m, k, u, v, c, i;
    scanf("%d", &t);
    while (t--) {
        memset(head, 0, sizeof(head)); qsz = 1;
        scanf("%d%d%d", &n, &m, &k);
        qk = k; qn = n;
        for (i=1; i<=m; ++i) {
            scanf("%d%d%d", &u, &v, &c);
            add(u, v, (ll)c);
        }
        printf("%lld\n", Dij(n));
    }
    
    return 0;
}