2.1.2BCD码

BCD码

BCD:用二进制编码的十进制

每四个二进制数对应16种状态的十种，还剩下6种

1.1 8421码的映射关系：

985十进制数在计算机中是用：1001 1000 0101二进制位保存的

计算机中5+8 是怎么样计算的 ？

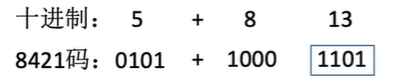
但是在8421码中没有1101这个范围，8421码中1010~1111是没有定义的

计算机如何处理呢

8421码映射关系只有0-15，在10-15的区间里，就需要加上一个6，让16进制进一个1，这样就能得到

9+9（十进制）=1001+1001=10010 但是8421码里面没有表示10010的数， 于是继续加一个6（0110），

10010+0110=1 1000=0001（前面不足四位补了3个0）+1000=18

1.2 余3码

余3码：8421码+3（0011)二进制

eg：8421码0（0000）所对应的余3码=8421码加上一个3=0000+0011=0101

余3码对应的十进制数是规定的，并不能像8421码能直接算出来，所以是无权码

1.3 有权码和无权码的区别

区别就是每一位是否有权值，如果有权值就能直接计算出对应的十进制

比如8421码 “0101”=0x2³+1x2²+0x2¹+1x2⁰=5 8421的权值就是8（2³）、4（2²）、2（2¹）、2⁰（1）

但是余3码就没有 权值不能直接算出十进制数

1.4 2421码

2、4、2、1分别代表每一位的权值

eg：0011 根据权值 0（2）+0（4）+1（2）+1（1）=2+1=3

但是这样有可能一个数可以由多个编码组成，比如5 可以是（1011）也可以是（0101）为了保证唯一性

0-4范围内为0开头 5-9为1开头，这样就保证了连续性