第四次作业
第四次作业
1.本章学习总结
1.1 思维导图
1.2 本章学习体会及代码量学习体会
1.2.1 学习体会
数组的使用让写代码更加简便,但相对之前的学习来说更需要理解,因此思路尤其重要
作业难度的提升,使学习更具有挑战性
需要更多的练习来熟练的掌握数组的应用方法
1.2.2 代码累计
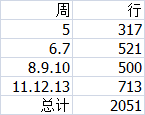
2.PTA总分



3.PTA实验作业
3.1PTA题目1
7-8 找出不是两个数组共有的元素 (20 分) 给定两个整型数组,本题要求找出不是两者共有的元素。 输入格式: 输入分别在两行中给出两个整型数组,每行先给出正整数N(≤20),随后是N个整数,其间以空格分隔。 输出格式: 在一行中按照数字给出的顺序输出不是两数组共有的元素,数字间以空格分隔,但行末不得有多余的空格。题目保证至少存在一个这样的数字。同一数字不重复输出。
3.1.1算法分析
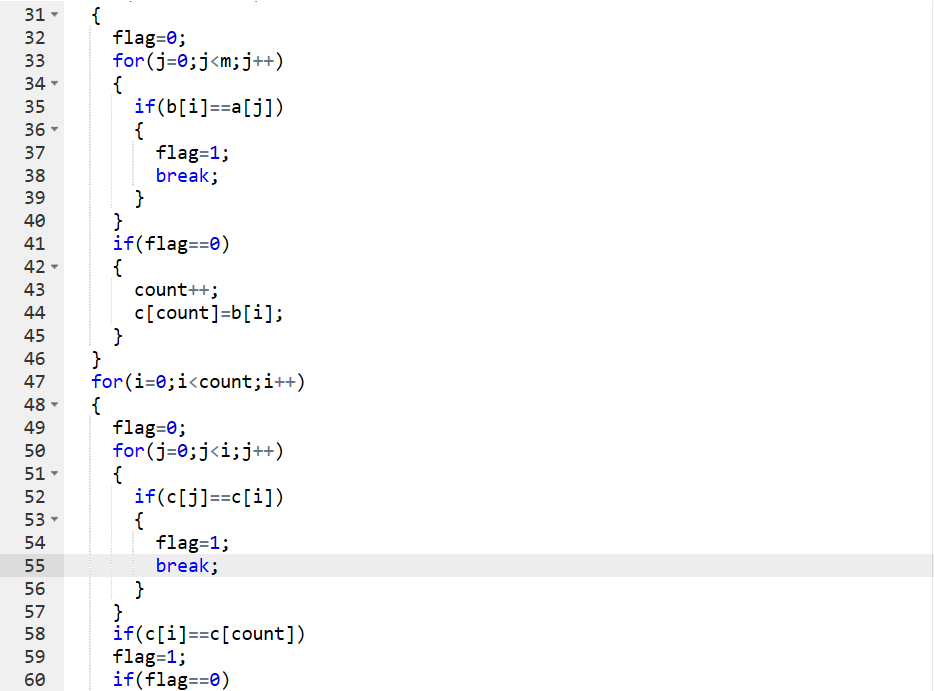
定义数组c[40],m,n,i,j,count=-1,flag
输入第一行个数m
定义数组a[m]用于存放第一行的数
for i=0 to i=m-1 do
输入第一行的数
end for
输入第二行个数n
定义数组b[n]用于存放第二行的数
for i=0 to i=n-1 do
输入第二行的数
end for
for i=0 to i=m-1 do //将a数组中有b数组中没有的数存入c数组中
flag=0
for j=0 to j=n-1 do
if a[i]=b[j] then
flag=1
break
end for
if flag=0 then
count++
c[count]=a[i]
end for
for i=0 to i=n-1 do //将b数组中有a数组中没有的数存入c数组中
flag=0
for j=0 to j=m-1 do
if b[i]=a[j] then
flag=1
break
end for
if flag=0 then
count++
c[count]=a[i]
end for
for i=0 to i=count-1 do //c数组中有重复的数据不多输出
for j=0 to j=i-1 do
if c[j]=c[i] then
flag=1
break
end for
if c[i]=c[count] then //与最后一个数据相等的都不输出
flag=1
if flag=0 then
输出c[i]
end for
输出c[count]
3.1.2代码截图


3.1.3 PTA提交列表及说明

一次通过
3.2题目二
7-5 螺旋方阵 (20 分)
所谓“螺旋方阵”,是指对任意给定的N,将1到N×N的数字从左上角第1个格子开始,按顺时针螺旋方向顺序填入N×N的方阵里。本题要求构造这样的螺旋方阵。
3.2.1算法分析
int a[10][10]
输入n,确定要输出的行列数
while (n*n!=c)
while(j+1<n&&!a[i][j+1])//从右向左开始递增
a[i][++j] = ++c; end while
while(i+1<n&&!a[i+1][j])//从上向下开始递增
a[++i][j]=++c;end while
while(j-1>=0&&!a[i][j-1])// 从右向左开始递增
a[i][--j]=++c;end while
while(i-1>=0&&!a[i-1][j])// 从下向上开始递增
a[--i][j]=++c;end while
end while
输出数组
3.2.2代码截图

3.2.3 PTA提交列表及说明

3.3题目三
一个IP地址是用四个字节(每个字节8个位)的二进制码组成。请将32位二进制码表示的IP地址转换为十进制格式表示的IP地址输出。```
###3.3.1算法分析
```c
定义数组字符型a[100],sum[100]
输入a[100]
定义i
for i=0 i<4 i++
定义number为0
定义m
for m=7 m>=0 m--
number+=(a[i*8+m]-'0')*(int)pow(2,7-m);计算对应地址的值
sum[i]=number 储存该值
输出sum数组
3.3.2代码截图

3.3.3PTA提交列表及说明

在计算公式上出现一些问题
4.代码互评
4.1代码截图
7-2 杨辉三角 (10 分)
打印n行杨辉三角,n<10。```
我的代码

同学代码

##4.2二者的不同
在对特殊情况的处理不同

