[LeetCode] 304. Range Sum Query 2D - Immutable
Medium
Given a 2D matrix matrix, find the sum of the elements inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

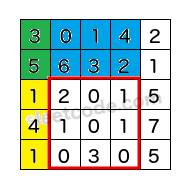
The above rectangle (with the red border) is defined by (row1, col1) = (2, 1) and (row2, col2) = (4, 3), which contains sum = 8.
Example:
Given matrix = [ [3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5] ] sumRegion(2, 1, 4, 3) -> 8 sumRegion(1, 1, 2, 2) -> 11 sumRegion(1, 2, 2, 4) -> 12
Note:
- You may assume that the matrix does not change.
- There are many calls to sumRegion function.
- You may assume that row1 ≤ row2 and col1 ≤ col2.
题目大意:给定一个矩形的左上角坐标和右下角坐标,计算这个矩形中各个元素之和。
方法:
使用动态规划的思想,维护一个二维数组dp,令每个单元都是以其为右下角的矩形的单元格之和。那么在给定左上角的情况下,用右下角的值减去左边界以左的矩形和上边界以上的矩形,再加上左上角重复减掉的矩形就是目标矩形了。
如下图,红色方框中的矩形单元和=以右下角零为右下角的大矩形-黄色矩形-蓝色矩形+重复减掉的绿色矩形。
在求数组dp时,对于边缘,我们要先初始化dp的第一行和第一列为0,所以dp比matrix要多一行一列。每个单元格的值=上+左-左上。具体实现代码如下:
因为需要私有变量dp,但是在dp定义的时候不能确定dp的大小,需要在构造函数里确定dp的大小,所以这里用了一个resize来修改二维向量的大小。
class NumMatrix { public: NumMatrix(vector<vector<int>>& matrix) { if(matrix.empty() || matrix[0].empty())return; int n=matrix.size(),m=matrix[0].size(); dp.resize(n+1,vector<int>(m+1,0)); for(int i=1;i<=n;++i){ for(int j=1;j<=m;++j){ dp[i][j]=matrix[i-1][j-1]+dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]; } } return; } int sumRegion(int row1, int col1, int row2, int col2) { int res=0; res=dp[row2+1][col2+1]-dp[row2+1][col1]-dp[row1][col2+1]+dp[row1][col1]; return res; } private: vector<vector<int>> dp; };


 浙公网安备 33010602011771号
浙公网安备 33010602011771号