后缀数组 模板+详解
后缀数组理解起来挺难的......
首先得学一下基数排序。
比如说下面这组数据:11,12,23,15,34,24
基数排序的第一关键字:十位数,第二关键字:个位数。
我们先对第一关键字也就是十位数开个桶hs[]计数:
记完之后应该是这个样子:hs[1]=3,hs[2]=2,hs[3]=1
这些数代表了十位数为k的数分别有多少个。
然后求一遍前缀和:hs[1]=3,hs[2]=5,hs[3]=6
不难发现,这时的hs[k]代表十位上为k的若干数中,排名最大的数的排名。
其实仔细想一想也能明白其中的原理。
那么知道了这些,我们下一步就是利用个位数,求出最终排名。
因为hs[k]代表十位上为k的若干数中,排名最大的数的排名。
所以我们从大到小枚举个位数。
设rk[k]为k的排名(k=11,12,23,15,34,24)。
- 个位数:5。个位是5的数有一个:15,十位上是1,
此时hs[1]=3,hs[2]=5,hs[3]=6,所以rk[15]=hs[1]=3。
十位为1的数已经用了一个,hs[1]--;
- 个位数:4。个位是4的数有两个:24、34,十位上分别是2和3,
此时hs[1]=2,hs[2]=5,hs[3]=6,所以rk[24]=hs[2]=5,rk[34]=hs[3]=6。
十位为2、3的数分别用了一个,hs[2]--,hs[3]--;
- 个位数:3。个位是3的数有一个:23,十位上是2,
此时hs[1]=2,hs[2]=4,hs[3]=5,所以rk[23]=hs[2]=4。
十位为2的数又用了一个,hs[2]--;
- 个位数:2。个位是2的数有一个:12,十位上是1,
此时hs[1]=2,hs[2]=3,hs[3]=5,所以rk[12]=hs[1]=2。
十位为1的数也用了一个,hs[1]--;
- 个位数:1。个位是1的数有一个:11,十位上是1,
此时hs[1]=1,hs[2]=3,hs[3]=5,所以rk[11]=hs[1]=1。
十位为1的数用了一个,hs[1]--;
结束了。基数排序就是这样。
接下来进入后缀数组的讲解。
我们设rk[i]为i开始的后缀的排名,sa[i]表示排名为i的后缀的开始位置,它们互为逆运算。
再开两个数组tr[]为暂时排名,hs[]为基数排序的桶。
为了避免出现空字符带来的麻烦,先将字符串倍长,n+1~2n的部分为“空”,“空”的字典序小于其它所有字符。
我们先求出s[1:1],s[2:2],s[3:3]......的相对排名,进而求出s[1:2],s[2:3],s[3:4],s[4:5]......的,
再求出s[1:4],s[2:5],s[3:6]......的,再求出s[1:8],s[2:9],s[3:10]......的......
这样倍增下去,最后直到没有排名相等的了,我们也就求出了所有后缀的相对排名。
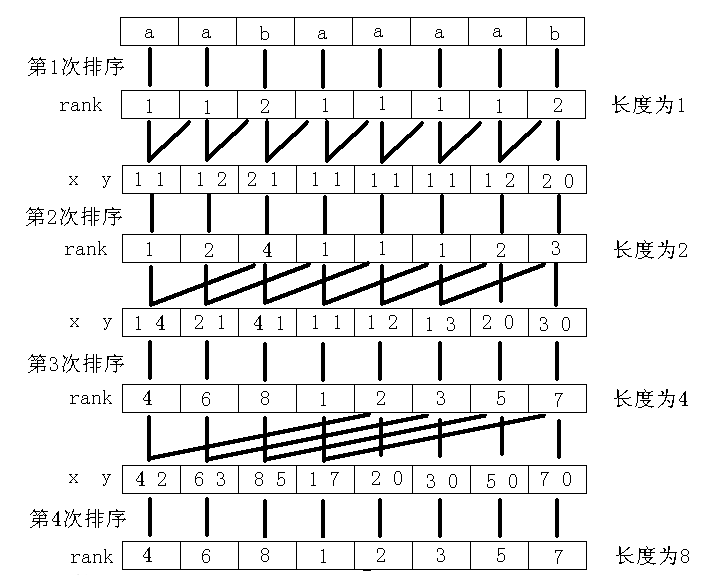
代码的具体思路:
先预处理一下rk[]和sa[],再倍增。
每次倍增先把桶清空,做一遍基数排序,记录sa[],最后判重地(也就是允许两个部分排名相等)计算排名。
反观tr[],tr[]显然与rk[]不同,tr[]是基数排序的直接结果,不会出现两个部分排名相同。
我们用tr[]更新sa[]之后,判重地计算rk[]来代替tr[]。
直到辅助记录排名的cnt==n,也就是说每个部分(s[1:1+2^k-1] , s[2:2+2^k-1] , s[3:3+2^k-1] ......)都对应了不同的排名,算法结束。
1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 using namespace std; 5 6 int n; 7 char s[1000005]; 8 int rk[1000005],sa[1000005]; 9 int tr[1000005],hs[1000005]; 10 int ht[1000005]; 11 12 int cmp(int x,int y,int k) 13 { 14 if(x+k>n||y+k>n)return 0; 15 return rk[x]==rk[y]&&rk[x+k]==rk[y+k]; 16 } 17 18 int main() 19 { 20 scanf("%s",s+1); 21 n=strlen(s+1); 22 int i,cnt; 23 for(i=1;i<=n;i++)hs[s[i]]++; 24 for(i=1,cnt=0;i<128;i++)if(hs[i])tr[i]=++cnt; 25 for(i=1;i<128;i++)hs[i]+=hs[i-1]; 26 for(i=1;i<=n;i++)rk[i]=tr[s[i]],sa[hs[s[i]]--]=i; 27 for(int k=1;cnt!=n;k<<=1) 28 { 29 for(i=1;i<=n;i++)hs[i]=0; 30 for(i=1;i<=n;i++)hs[rk[i]]++; 31 for(i=1;i<=n;i++)hs[i]+=hs[i-1]; 32 for(i=n;i;i--)if(sa[i]>k)tr[sa[i]-k]=hs[rk[sa[i]-k]]--; 33 for(i=1;i<=k;i++)tr[n-i+1]=hs[rk[n-i+1]]--; 34 for(i=1;i<=n;i++)sa[tr[i]]=i; 35 for(i=1,cnt=0;i<=n;i++)tr[sa[i]]=cmp(sa[i],sa[i-1],k)?cnt:++cnt; 36 for(i=1;i<=n;i++)rk[i]=tr[i]; 37 } 38 for(i=1;i<=n;i++)printf("%d ",sa[i]); 39 return 0; 40 }
在后缀数组的基础上,还能求出height数组。
height[i] 记录排名为 i 的后缀与排名为 i-1 的后缀的LCP(最长公共前缀)。
而且height[ i ] <= height[ rank[ sa[ i ] + 1] ] + 1。
所以我们可以按原串中开始位置从前到后的顺序求height 数组。
求height[rank[i]] 时,只需从 height[ rank[ i - 1] ] - 1 开始枚举就行了。
1 for(i=1;i<=n;i++) 2 { 3 if(rk[i]==1)continue; 4 for(int j=max(1,ht[rk[i-1]]-1);;j++) 5 { 6 if(s[i+j-1]==s[sa[rk[i]-1]+j-1])ht[rk[i]]=j; 7 else break; 8 } 9 }
求出height数组之后,我们就可以求两个后缀的LCP了。
可以发现,对于j、k,不妨设rk[j]<rk[k]
则LCP(j,k)=min( height[ rk[ j ] + 1 ] , height[ rk[ j ] + 2 ] , height[ rk[ j ] + 3 ]......height[ rk[ k ] ] )。
套一个RMQ求区间最小值就行。
显然我们还可以由此求两个子串的LCP。
一个字符串任意两个子串s[j1 : k1]、s[j2 : k2] 的LCP就是
min(LCP(suffix[j1],suffix[j2]),k1 - j1 + 1,k2 - j2 + 1)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号