[洛谷P3391] 文艺平衡树 (Splay模板)
初识splay
学splay有一段时间了,一直没写......
本题是splay模板题,维护一个1~n的序列,支持区间翻转(比如1 2 3 4 5 6变成1 2 3 6 5 4),最后输出结果序列。
模板题嘛......主要了解一下splay的基本操作QwQ
1.基本概念
splay是一种二叉搜索树,节点的权值满足lson<p<rson,故可以像其他二叉搜索树一样在树上二分查找某数排名,排名为k的数,以及前驱后继等。
普通的二叉搜索树在面对特殊数据时树的深度会从log n退化成接近n(退化成链),这样操作的时间复杂度会从O(log n)退化成O(n),影响效率。
splay通过旋转维持树的平衡。这个操作后面会提到。
2.基本操作
二叉搜索树的基本操作:求排名为k的数。
1 int rank(int p,int k) 2 { 3 pushdown(p); 4 if(k<=sz[s[p][0]]) 5 return rank(s[p][0],k); 6 else if(k==sz[s[p][0]]+1) 7 return p; 8 else 9 return rank(s[p][1],k-sz[s[p][0]]-1); 10 }
简单的树上二分。
3.核心操作:splay
splay的精髓在于骚气的旋转。(名字就是这么来的哈哈哈~)
splay的核心操作是splay(一脸懵逼),splay(x,y)意为通过一系列旋转,将点x旋转到点y下面,使x成为y的儿子。
每次旋转通过rotate函数实现:
1 void rotate(int p) 2 { 3 int fa=f[p]; 4 bool k=id(p); 5 s[fa][k]=s[p][!k]; 6 s[p][!k]=fa; 7 s[f[fa]][id(fa)]=p; 8 f[p]=f[fa]; 9 f[s[fa][k]]=fa; 10 f[fa]=p; 11 refresh(fa); 12 refresh(p); 13 }
rotate的时候严格满足splay二叉搜索树的性质:lson<p<rson。
将p提到fa的位置,根据大小关系决定fa是作为p的左儿子还是右儿子,这样实际上是fa挤掉了p原先的某个儿子,而p转上去,让出了fa的一个儿子的位置。
所以最后让那个被fa挤掉的p的孤儿作为fa的某个儿子,填到空缺的地方去(原来p的位置)。
至于splay的实现方法...有两种:单旋和双旋。
单旋即无脑地一直转,直到把x转到y下面。
1 void splay(int p,int g) // 单旋 2 { 3 while(f[p]!=g)rotate(p); 4 if(!g)root=p; 5 }
比起单旋,双旋能更好的维护splay的平衡。
1 void splay(int p,int g) // 双旋 2 { 3 while(f[p]!=g) 4 { 5 int fa=f[p]; 6 if(f[fa]==g) 7 { 8 rotate(p); 9 break; 10 } 11 if(id(p)^id(fa))rotate(p); 12 else rotate(fa); 13 rotate(p); 14 } 15 if(!g)root=p; 16 }
利用splay操作,我们就可以用这棵树实现很多其它平衡树实现不了的功能。
4.元素的插入、删除、查询及修改
设x为 要插入的/要删除的/要查询的/要修改的 元素or区间。
进行这些操作之前,运用旋转操作把x的前驱pre转到根位置,把x的后继post转到根的下面,post>pre,所以此时post一定是pre的右儿子。
(如果是区间,pre就是left的前驱,post就是right的后继)
如图:
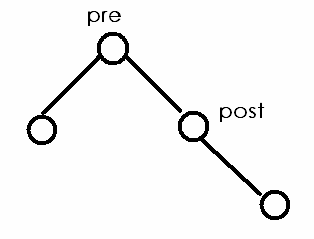
此时,根据二叉搜索树的性质,要删除/查询/修改的元素or区间就一定在post的左子树那里。如图:(目标子树:红色部分)
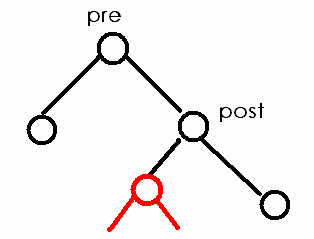
4.1 插入
如果是插入,红色部分一定为空,在那里插入即可。
4.2 删除
残忍抛弃红色部分。
4.3 查询
在红色部分查询。
4.4 修改
在这道题里是区间翻转。
我们并不需要真的翻转,打个标记就行。
标记需要下传的时候,交换左右子树的左右子树,在左右儿子上打标记,清掉自身标记。
1 void pushdown(int p) 2 { 3 if(!fl[p])return; 4 fl[s[p][0]]^=1; 5 fl[s[p][1]]^=1; 6 swap(s[s[p][0]][0],s[s[p][0]][1]); 7 swap(s[s[p][1]][0],s[s[p][1]][1]); 8 fl[p]=0; 9 }
这样就行了。
完事了?
完事了。
最后二分输出序列即可。
其他细节见代码。

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #define N 100005 5 #define id(x) (s[f[x]][1]==x) // 判断是左儿子还是右儿子 6 using namespace std; 7 8 int f[N],s[N][2],val[N],sz[N],root,tot; // 分别是父亲,儿子,值,子树大小,树根,元素数量 9 bool fl[N]; // 翻转标记 10 11 void refresh(int p) // 更新size 12 { 13 sz[p]=sz[s[p][0]]+sz[s[p][1]]+1; 14 } 15 16 void pushdown(int p) // 下传标记 17 { 18 if(!fl[p])return; 19 fl[s[p][0]]^=1; 20 fl[s[p][1]]^=1; 21 swap(s[s[p][0]][0],s[s[p][0]][1]); 22 swap(s[s[p][1]][0],s[s[p][1]][1]); 23 fl[p]=0; 24 } 25 26 void rotate(int p) // 把p转上去 27 { 28 int fa=f[p]; 29 bool k=id(p); 30 s[fa][k]=s[p][!k]; 31 s[p][!k]=fa; 32 s[f[fa]][id(fa)]=p; 33 f[p]=f[fa]; 34 f[s[fa][k]]=fa; 35 f[fa]=p; 36 refresh(fa); 37 refresh(p); 38 } 39 /* 40 void splay(int p,int g) // 单旋 41 { 42 while(f[p]!=g)rotate(p); 43 if(!g)root=p; 44 } 45 */ 46 void splay(int p,int g) // 双旋 47 { 48 while(f[p]!=g) 49 { 50 int fa=f[p]; 51 if(f[fa]==g) 52 { 53 rotate(p); 54 break; 55 } 56 if(id(p)^id(fa))rotate(p); 57 else rotate(fa); 58 rotate(p); 59 } 60 if(!g)root=p; 61 } 62 63 int rank(int p,int k) // 查询rank为k的元素 64 { 65 pushdown(p); 66 if(k<=sz[s[p][0]]) 67 return rank(s[p][0],k); 68 else if(k==sz[s[p][0]]+1) 69 return p; 70 else 71 return rank(s[p][1],k-sz[s[p][0]]-1); 72 } 73 74 int build(int l,int r,int fa) // 建树 实际上一个一个插入也行,但是这样二分建树可以使初始树更平衡 75 { 76 if(l>r)return 0; 77 int mid=(l+r)>>1; 78 int p=++tot; 79 s[p][0]=build(l,mid-1,p); 80 s[p][1]=build(mid+1,r,p); 81 val[p]=mid; 82 f[p]=fa; 83 refresh(p); 84 return p; 85 } 86 87 void change(int l,int r) // 区间翻转 88 { 89 int pre,post,rt; 90 pre=rank(root,l-1); 91 splay(pre,0); 92 post=rank(root,r+1); 93 splay(post,pre); 94 rt=s[post][0]; 95 swap(s[rt][0],s[rt][1]); 96 fl[rt]^=1; 97 } 98 99 void print(int p) // 二分输出结果序列 100 { 101 if(!p)return; 102 pushdown(p); 103 print(s[p][0]); 104 printf("%d ",val[p]); 105 print(s[p][1]); 106 } 107 108 int n,m; 109 110 int main() 111 { 112 scanf("%d%d",&n,&m); 113 root=build(0,n+1,0); 114 for(int i=1;i<=m;i++) 115 { 116 int lb,rb; 117 scanf("%d%d",&lb,&rb); 118 change(lb+1,rb+1); 119 } 120 splay(rank(root,1),0); 121 splay(rank(root,n+2),root); 122 print(s[s[root][1]][0]); 123 return 0; 124 } 125 126 complete code of splay tree



