照相机标定——棋盘格
照相机标记步骤：
1.制作棋盘格（每个格子的大小可测量），最好是打印出来，贴在平面上（实在不行就用我刚才演示的黑白棋盘格方法）
2.根据棋盘格，采集10-20张图片，提取角点
3.解算出内外参数，内参截图放在博客中，外部参数最好能可视化
一、棋盘格选定:
规格:10cm×10cm（5×5） 每个方格2cm×2cm
手机型号:vivoy67 相机分辨率:1300×1600
二、棋盘格的Harris角点检测
首先Harris 角点检测是基于图像像素灰度值变化梯度的，灰度值图像的角点附近，是其像素灰度值变化非常大的区域，其梯度也非常大。换句话说，在非角点位置邻域里，各点的像素值变化不大，甚至几乎相等，其梯度相对也比较小。如果邻域内点的灰度值与中心点Image (i,j) 的灰度值之差 的绝对值 在一个阈值t 范围 内，那就认为这个点与中心点是相似的。与此同时，属于该 Image(i,j) 点的相似点计数器nlike(i,j) 也随之加1。在 Image (i,j) 点的n 邻域 全部被遍历一边之后，就能得到在这个邻域范围内与中心点相似的 点个数的统计值nlike(i,j) 。根据nlike(i,j) 的大小，就可以判断这个中心点是否可能为角点。由于选择3*3的检测窗口，所以，对于中心像素点 , 在下面的讨论中只考虑其8 邻域内像素点的相似度。算该范围的像素点与中心像素点的灰度值之差的绝对值 (记为 Δ ) , 如果该值小于等于设定的阈值 ( 记为 t) , 则认为该像素点与目标像素点相似。
nlike(i,j)=sum(R(i+x,j+y))(-1≤x≤1,-1≤y≤1,且 x≠0 , y≠0) ,其中 : R(i+x, j+y)=1 , 当Δ(i+x , j+y)≤t
R(i+x,j+y)=0 , 当Δ(i+x , j+y)>t
从定义中可以看出 : 0≤nlike (i,j)≤8。现在讨论nlike( i , j) 值的含义 。
(1) nlike (i , j) = 8 ,表示当前中心像素点的 8邻域范围内都是与之相似的像素点 , 所以该像素点邻域范围内的梯度不会很大 , 因此角点检测时 , 应该排除此类像素点，不将其作为角点的候选点 。
(2) nlike (i , j) = 0 ,表示当前中心像素点的 8邻域范围内没有与之相似的像素点 , 所以该像素点为孤立像素点或者是噪声点 , 因此角点检测时 , 也应该排除此类像素点 。
(3) nlike (i , j) = 7 ,可以归结为以下的两者情况 ,其他情形都可以通过旋转来得到 ( 图中黑色区域仅表示与中心像素相似 , 而两个黑色区域像素可能是相似的 , 也可能不相似 )
(4) nlike (i , j) = 1 , 中心像素点也不可能为角点 。
(5) 2≤ nlike ( i , j) ≤ 6 , 情况比较复杂 , 无法确认像素点准确的性质。我采取的方法是先将其列入候选角点之列，对其进行计算角点响应CRF等后续操作。
然后计算各候选角点的CBF，进行非极大抑制，再次由于Harris算子不具有尺度不变性，为确保角点检测的准确度和完整性，我们采用Mikolajczyk和Schmid提出的Harris - Laplace检测方法[8]，将Harris算子与高斯尺度空间相结合，从而克服Harris 算子只能在单一尺度下检测角点的缺点
代码:
#include <iostream>
#include <opencv2/opencv.hpp>
int main(int argc, char *argv[])
{
int blockSize = 2;
int kSize = 3;
double k = 0.04;
double thread_value = 85; // R的阈值
cv::Mat orignal_image = cv::imread (argv[1]);
cv::Mat gray_image , after_harris_image;
cv::Mat norm_image; //归一化后的图
cv::Mat scaled_image; //线性变换后的八位无符号整形的图
cv::cvtColor (orignal_image,gray_image,CV_BGR2GRAY); // 灰度变换
cv::cornerHarris(gray_image, after_harris_image, blockSize, kSize, k, cv::BORDER_DEFAULT); //harris corner detect
cv::normalize(after_harris_image, norm_image, 0, 255, cv::NORM_MINMAX, CV_32FC1, cv::Mat()); //归一化处理
convertScaleAbs(norm_image, scaled_image);
for (int i = 0; i < norm_image.rows; i++)
{
for (int j = 0; j < norm_image.cols; j++)
{
if ((int)norm_image.at<float>(i, j) > thread_value)
{
cv::circle(orignal_image, cv::Point(j, i), 10, cv::Scalar(10, 10, 255), 1, 8, 0); //tag the corner
}
}
}
cv::imshow("after_harris_corner", orignal_image);
cv::imwrite("after_harris_corner.png",orignal_image);
cv::waitKey(0);
return 0;
}
检测结果:
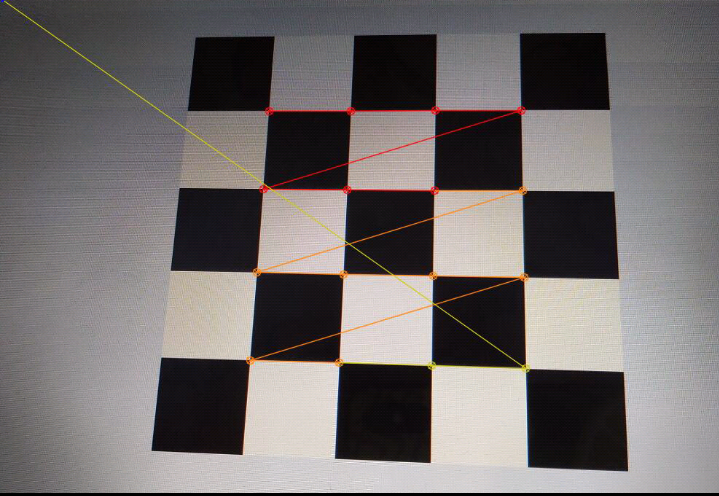
小结:
基于图像灰度的角点检测和图像边缘提取的角点检测，其中后一种依赖于图像边缘提取的好坏，实用性不是很强。其中Harris的定位性能和鲁棒性较好，加之Harris算法原理简单，不受摄像机姿态和光照的影响，现已成为了使用最为广泛的角点提取算法之一。因此，针对Harris算法现在也已提出了许多改进算法：亚像素级的角点检测算法与尺度空间相结合的算法，自适应角点提取算法根据棋盘格的几何特性提出的检测算法等，但大部分都是以增加计算量或者低效率为代价，同时，用 Harris 算法进行检测，有三点不足：（1 ）该算法不具有尺度不变性；（2 ）该算法提取的角点是像素级的；（3 ）该算法检测时间不是很令人满意。
三、求解内参数矩阵:
单应性：在计算机视觉中被定义为一个平面到另一个平面的投影映射。首先确定，图像平面与标定物棋盘格平面的单应性。设三维世界坐标的点为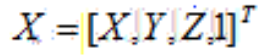
二维相机平面像素坐标为
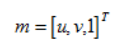，所以标定用的棋盘格平面到图像平面的单应性关系为:
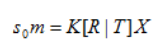(其中，K为相机的内参矩阵，R为外部参数矩阵（旋转矩阵），T为平移向量。令
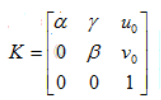，设棋盘格位于Z=0的平面，定义旋转矩阵R的第i列为 ri, 则有：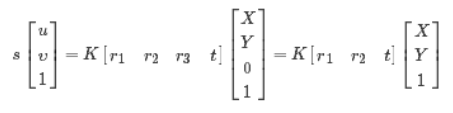
于是空间到图像的映射可改为：H=λK[r1 r2 t]
其中H 是描述Homographic矩阵,可通过最小二乘，从角点世界坐标到图像坐标的关系求解
根据步骤1中的式子，令H为H =[h1 h2 h3]，则[h1 h2 h3]=λK[r1 r2 t],再根据正交和归一化的约束可以得到等式:
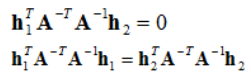
即每个单应性矩阵能提供两个方程，而内参数矩阵包含5个参数，要求解，至少需要3个单应性矩阵。为了得到三个不同的单应性矩阵，我们使用至少三幅棋盘格平面的图片进行标定。通过改变相机与标定板之间的相对位置来得到三个不同的图片。为了方便计算，我们定义:
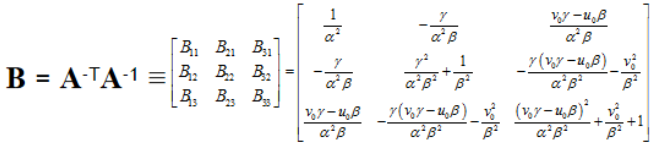
B中的未知量可表示为6D向量b,设H中的第列为h;根据b的定义，可以推导出公式
最后推到出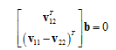
通过上式，我们可知当观测平面n≥3时，即至少3幅棋盘格图像，可以得到b的唯一解，求得相机内参数矩阵K。
3、计算外参数矩阵:
外部参数可通过Homography求解，由 H = [h1 h2 h3] = λA[r1 r2 t]，可推出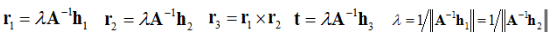
代码:
# coding=utf-8
import numpy as np
import cv2
import glob
# 终止标准
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
#w = 6
#h = 6
#准备对象点，如（0,0,0），（1,0,0），（2,0,0）......，（6,5,0）
#objp = np.zeros((w*h,3), np.float32)
objp = np.zeros((4*4,3), np.float32)
objp[:,:2] = np.mgrid[0:4,0:4].T.reshape(-1,2)
# 用于存储所有图像中的对象点和图像点的数组。
objpoints = [] # 在现实世界空间的3d点
imgpoints = [] # 图像平面中的2d点。
#glob是个文件名管理工具
images = glob.glob('C:/B1/*.jpg')
print('...loading')
for fname in images:
#对每张图片，识别出角点，记录世界物体坐标和图像坐标
print('processing img:{fname}')
img = cv2.imread(fname)
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)#转灰度
print('grayed')
#寻找角点，存入corners，ret是找到角点的flag
#ret, corners = cv2.findChessboardCorners(gray, (w, h),None)
ret, corners = cv2.findChessboardCorners(gray, (4, 4),None)
# 如果找到，添加对象点，图像点（精炼后）
if ret == True:
print('chessboard detected')
objpoints.append(objp)
#执行亚像素级角点检测
corners2 = cv2.cornerSubPix(gray,corners,(11,11),(-1,-1),criteria)
imgpoints.append(corners2)
# 绘制并显示角点
#img = cv2.drawChessboardCorners(img, (w,h), corners2,ret)
img = cv2.drawChessboardCorners(img, (4,4), corners2,ret)
cv2.namedWindow('img',0)
cv2.resizeWindow('img', 500, 500)
cv2.imshow('img',img)
cv2.waitKey(500)
cv2.destroyAllWindows()
'''
传入所有图片各自角点的三维、二维坐标，相机标定。
每张图片都有自己的旋转和平移矩阵，但是相机内参和畸变系数只有一组。
mtx，相机内参；dist，畸变系数；revcs，旋转矩阵；tvecs，平移矩阵。
'''
img2 = cv2.imread("C:/B1/13.jpg")
print("type objpoints:{objpoints[0].shape}")
print("type imgpoints:{imgpoints[0].shape}")
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1],None,None)
h, w = img2.shape[:2]
'''
优化相机内参（camera matrix），这一步可选。
参数1表示保留所有像素点，同时可能引入黑色像素，
设为0表示尽可能裁剪不想要的像素，这是个scale，0-1都可以取。
'''
newcameramtx, roi=cv2.getOptimalNewCameraMatrix(mtx,dist,(w,h),1,(w,h))
#纠正畸变
dst = cv2.undistort(img2, mtx, dist, None, newcameramtx)
# 裁剪图像，输出纠正畸变以后的图片
x,y,w,h = roi
dst = dst[y:y+h, x:x+w]
cv2.imwrite('calibresult.png',dst)
#打印我们要求的两个矩阵参数
print ("newcameramtx外参:\n",newcameramtx)
print ("dist畸变值:\n",dist)
print ("newcameramtx旋转（向量）外参:\n",rvecs)
print ("dist平移（向量）外参:\n",tvecs)
#计算误差
tot_error = 0
for i in range(len(objpoints)):
imgpoints2, _ = cv2.projectPoints(objpoints[i], rvecs[i], tvecs[i], mtx, dist)
error = cv2.norm(imgpoints[i],imgpoints2, cv2.NORM_L2)/len(imgpoints2)
tot_error += error
print ("total error: ", tot_error/len(objpoints))
运行结果:
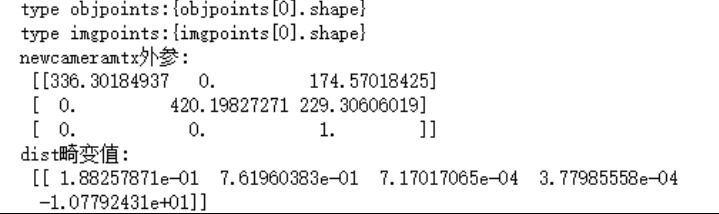
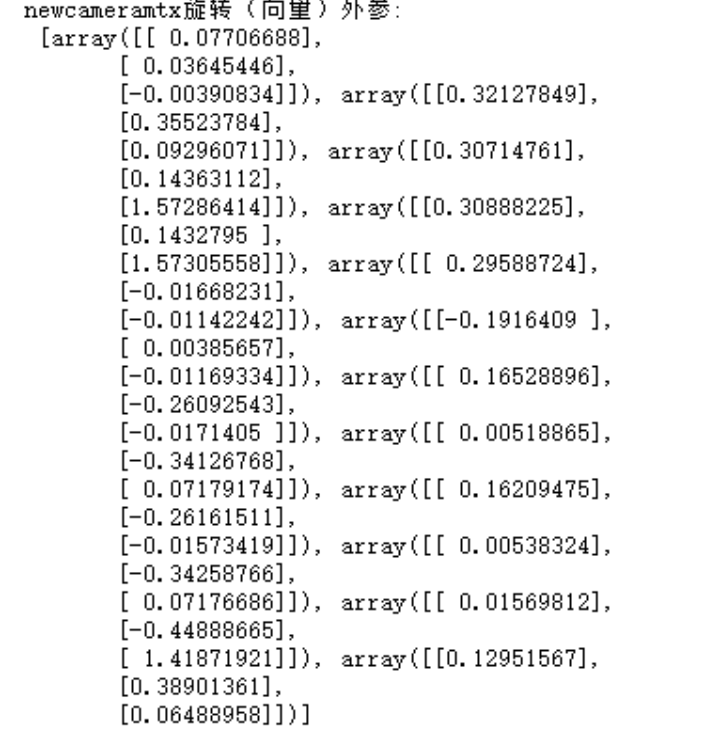
实验总结:
实验时要保证视场大小与标定板大小相当，或者稍微大一些，以保证在标定板平移时仍然在视场内。先把光圈调到最大进行对焦，对焦时要考虑到全场的清晰程度，达到一种全场的均衡。对焦完成后，把光圈减小，增加曝光，同时补光增加亮度，这样做是为了增加拍摄时的景深。关于标定板亮度，看灰度直方图，平均亮度在150可以，在180~200之间为宜，不能出现过曝。 其次是相机水平和对称问题，根据实验结果分析。要减小误差需要让双摄像机尽量与水平面平行，且两相机的y坐标尽量相同，左右摄像机关于中轴线对称。
