粒子群优化算法-参数寻优
一、粒子群算法的概念
粒子群优化算法的基本思想:是通过群体中个体之间的协作和信息共享来寻找最优解.
PSO的优势:在于简单容易实现并且没有许多参数的调节。目前已被广泛应用于函数优化、神经网络训练、模糊系统控制以及其他遗传算法的应用领域。
二、粒子群算法分析
1、基本思想
粒子群算法通过设计一种无质量的粒子来模拟鸟群中的鸟,粒子仅具有两个属性:速度和位置,速度代表移动的快慢,位置代表移动的方向。每个粒子在搜索空间中单独的搜寻最优解,并将其记为当前个体极值,并将个体极值与整个粒子群里的其他粒子共享,找到最优的那个个体极值作为整个粒子群的当前全局最优解,粒子群中的所有粒子根据自己找到的当前个体极值和整个粒子群共享的当前全局最优解来调整自己的速度和位置。
2、粒子群算法的主要步骤如下:
(1)对粒子群的随机位置和速度进行初始设定,同时设定迭代次数。第二步:计算每个粒子的适应度值。
(2)对每个粒子,将其适应度值与所经历的最好位置Pbest;的适应度值进行比较,若较好,则将其作为当前的个体最优位置。
(3)对每个粒子,将其适应度值与全局所经历的最好位置Gbestg的适应度值进行比较,若较好,则将其作为当前的全局最优位置。
(4)根据公式(1), (2)对粒子的速度和位置进行优化,从而产生新的粒子。
(5)如未达到结束条件(通常为最大循环数或最小误差要求),则返回第二步。
3、本案例群体的初始参数列表:
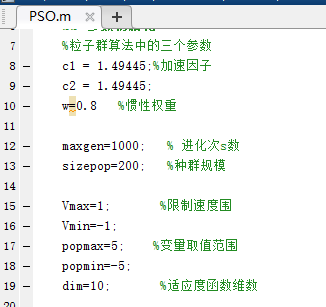
maxgen:一般为最大迭代次数以最小误差的要求满足的。粒子群算法的最大迭代次数,也是终止条件数。
c1,c2:加速常数,取随机2左右的值。
w:惯性权重产生的。
4、初始运行:
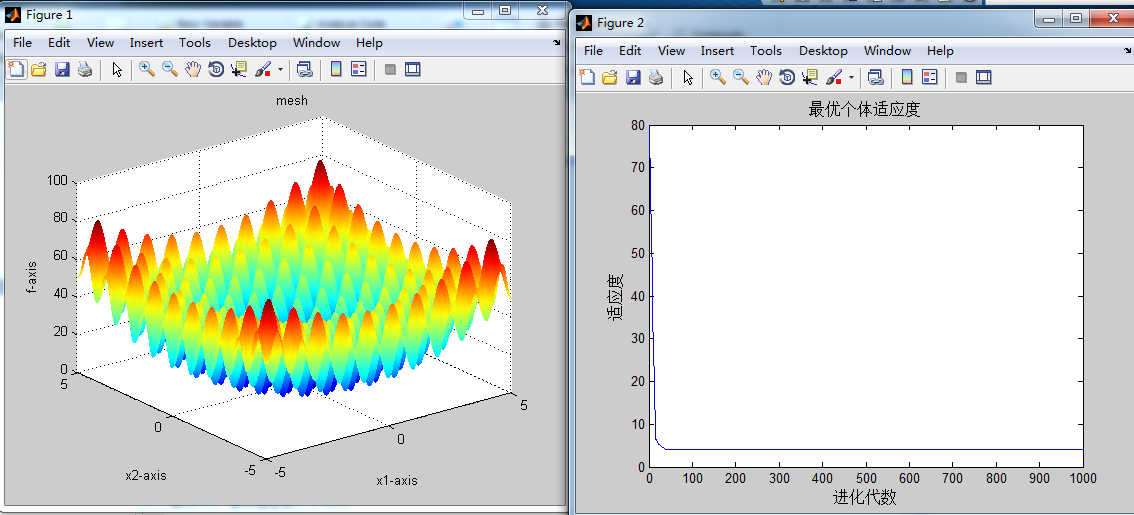
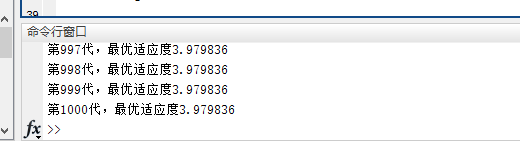
(1)首先测试c1、c2、w的迭代影响:
利用函数来表示各变量:

运行得:
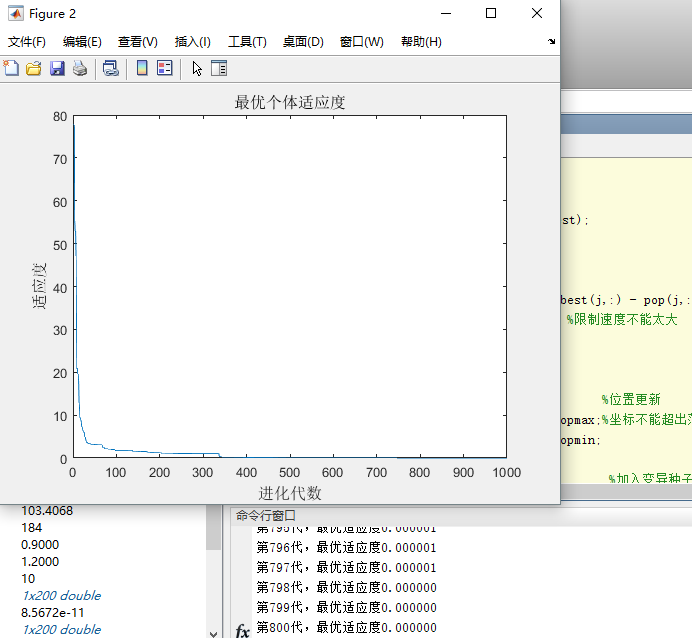
逐渐迭代得:
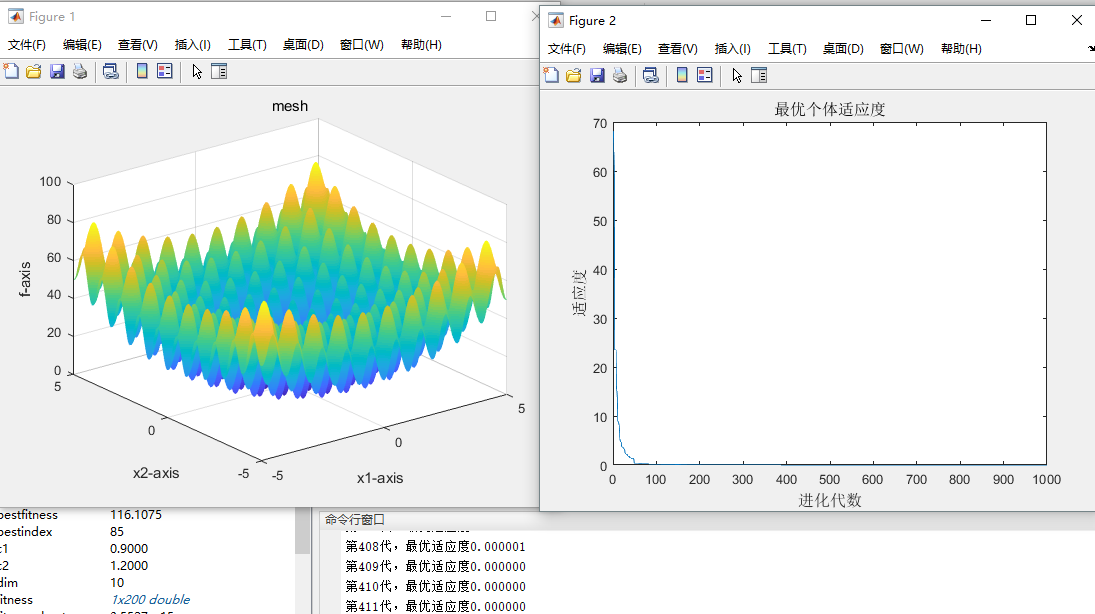
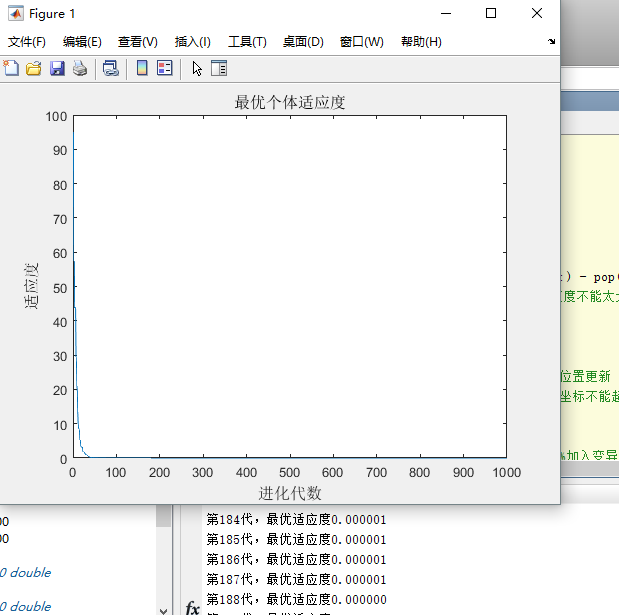
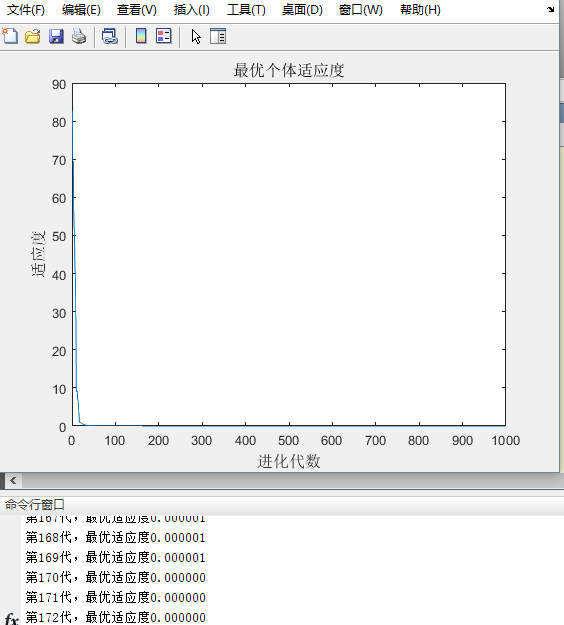
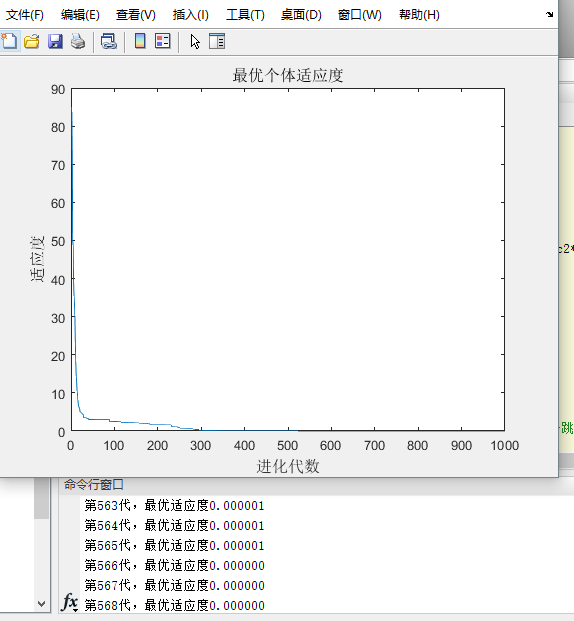
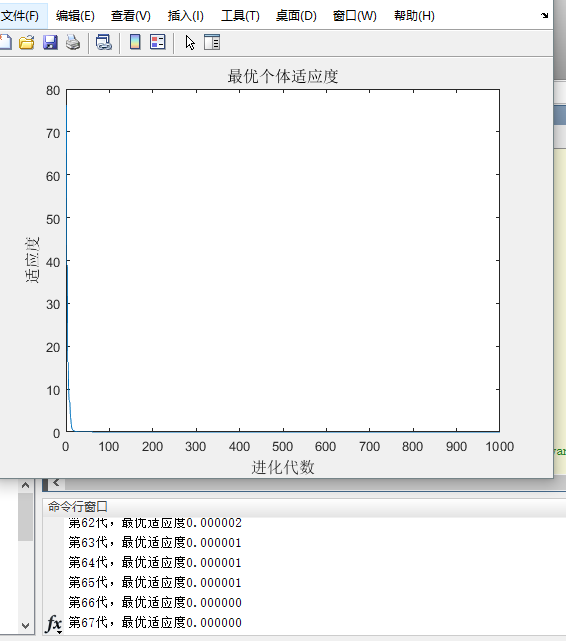
可以看出迭代收敛最早。随着不断的迭代,最优适应度承不稳定状态。
(2)dim与sizepop的影响:
适应度函数维数dim=12:
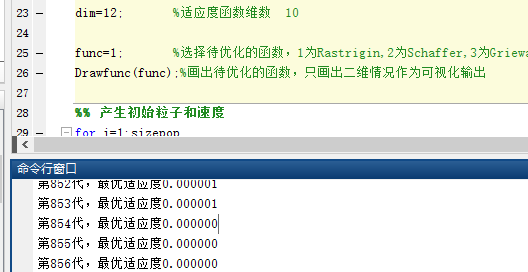
适应度函数维数dim=8:
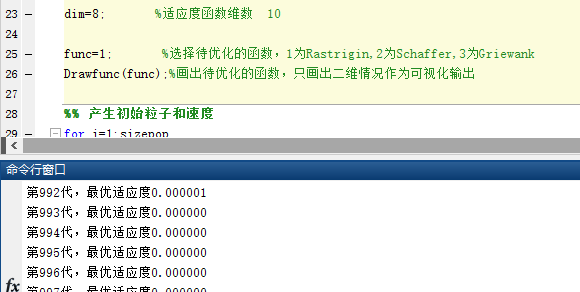
适应度函数维数dim=5:
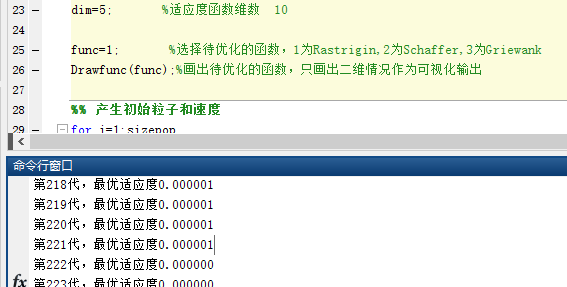
适应度函数维数dim=3:
种群规模sizepop=220:
种群规模sizepop=200:
种群规模sizepop=150:
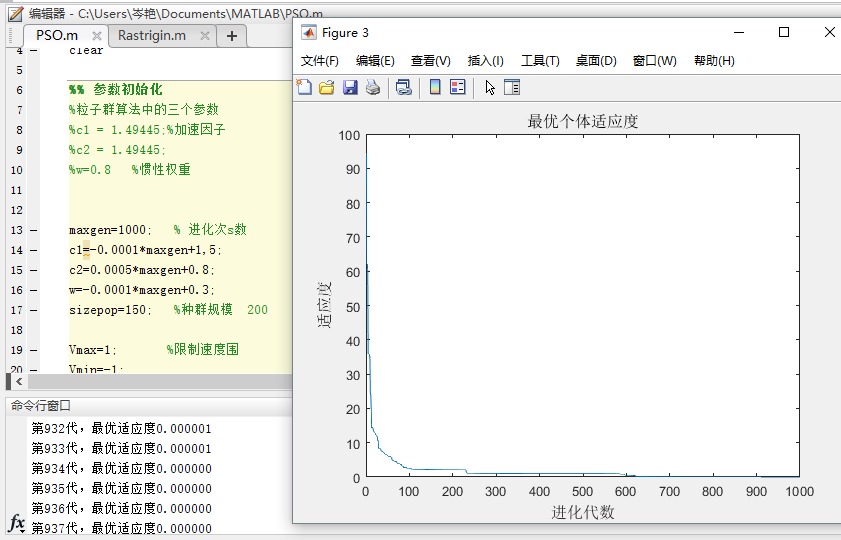
种群规模sizepop=130:
将种群规模sizepop调制到<130时,迭代次数无法收敛到接近于0,所以判别种群规模sizepop在200最佳。
结论:
较大的w有利于跳出局部极值。而较小的w有利于算法收敛。相较于传统算法计算速度非常快,全局搜索能力也很强;
对于适应度函数维数dim的不断改变值(初始值为10的情况下),分别测试>10和<10的迭代可以看出,dim的值越小,迭代收敛次数越小。最优值在3~5之间最佳。
PSO对于种群大小不十分敏感,所以初始种群往往设为500-1000,不同初值速度影响也不大;
粒子群算法适用于连续函数极值问题,对于非线性、多峰问题均有较强的全局搜索能力。

