蚂蚁算法实现旅行商问题
一、蚂蚁算法实现旅行商问题:
(一)问题描述
TSP问题可以用一个带权完全图G=(N,A)来表示,其中N是带有n=|N|点(城市)的集合,A是完全连接这些点的边的集合。每一条边(i,j)属于A都带有一个权值,它代表城市i与城市j之间的距离。TSP问题就是要找到图中的最短哈密尔顿回路。
1、构建图:构建图与问题描述图是一致的,成份的集合C对应着点的集合(即:C=N),连接对应着边的集合(即L=A),且每一条边都带有一个权值,代表点i和j之间的距离。
2、约束条件:所有城市都要被访问且每个城市最多只能被访问一次。
3、信息素和启发式信息:TSP 问题中的信息素表示在访问城市i后直接访问城市j的期望度。启发式信息值一般与城市i和城市j的距离成反比。
4、解的构建:每只蚂蚁最初都从随机选择出来的城市出发,每经过一次迭代蚂蚁就向解中添加一个还没有访问过的城市。当所有城市都被蚂蚁访问过之后,解的构建就终止。
蚁群算法的影响因素
(1)感知范围:蚂蚁观察到的范围是一个方格世界,相关参数为速度半径,因此可能陷入局部最优
(2)环境信息:蚂蚁所在环境中其他蚂蚁、信息素,还可能有障碍物,信息素以一定速率降低或消失。
(3)觅食规则:蚂蚁在感知范围内寻找食物,如果感知到就会过去,否则朝信息素多的地方移动
(4)移动规则:蚂蚁朝信息素最多的方向移动,当周围没有信息素指引时,会按照原来运动方向惯性移动。而且会记住最近走过的点,防止原地转圈。
(5)避障规则:当蚂蚁的移动方向有障碍物时,将随机选择其他方向;当有信息素指引时,将按照觅食规则移动。
(6)散发信息素规则:在刚找到食物或者窝时,蚂蚁散发的信息素最多;当随着走远时,散发的信息素将逐渐减少。
蚁群算法的实现
蚂蚁找到最短路径要取决于信息素和环境,假设有两条路可通向食物,开始时两条路上的蚂蚁数量差不多:当蚂蚁到达终点之后会立即返回,距离短的路上的蚂蚁往返一次时间短,重复频率快,在单位时间里往返蚂蚁的数目就多,留下的信息素也多,会吸引更多蚂蚁过来,会留下更多信息素。而距离长的路正相反,因此越来越多的蚂蚁聚集到最短路径上来。
蚂蚁的智能行为得益于其简单的行为规则,该规则让其具有多样性和正反馈。在觅食时,多样性使蚂蚁不会走进死胡同而无限循环,是一种创新能力;正反馈使优良信息保存下来,是一种学习强化能力。两者的巧妙结合使智能行为涌现,如果多样性过剩,系统过于活跃,会导致过多的随机运动,陷入混沌状态;如果多样性不够,正反馈过强,会导致僵化,当环境变化时蚁群不能相应调整
运算过程
1、蚂蚁在路径上释放信息素。
2、碰到还没走过的路口,就随机挑选一条路走。同时,释放与路径长度有关的信息素。
3、信息素浓度与路径长度成反比。后来的蚂蚁再次碰到该路口时,就选择信息素浓度较高路径。
4、最优路径上的信息素浓度越来越大。
5、最终蚁群找到最优寻食路径。
二、源代码:
%% 旅行商问题(TSP)优化
%% 清空环境变量
clear all
clc
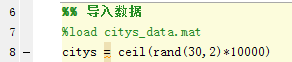
%% 导入数据
citys = ceil(rand(30,2)*10000)
load citys.mat
%% 计算城市间相互距离
fprintf('Computing Distance Matrix... \n');
n = size(citys,1);
D = zeros(n,n);
for i = 1:n
for j = 1:n
if i ~= j
D(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));
else
D(i,j) = 1e-4;
end
end
end
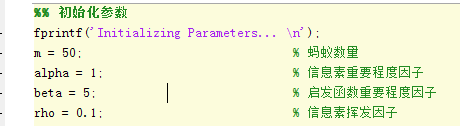
%% 初始化参数
fprintf('Initializing Parameters... \n');
m = 50; % 蚂蚁数量
alpha = 1; % 信息素重要程度因子
beta = 5; % 启发函数重要程度因子
rho = 0.1; % 信息素挥发因子
Q = 1; % 常系数
Eta = 1./D; % 启发函数
Tau = ones(n,n); % 信息素矩阵
Table = zeros(m,n); % 路径记录表
iter = 1; % 迭代次数初值
iter_max = 150; % 最大迭代次数
Route_best = zeros(iter_max,n); % 各代最佳路径
Length_best = zeros(iter_max,1); % 各代最佳路径的长度
Length_ave = zeros(iter_max,1); % 各代路径的平均长度
%% 迭代寻找最佳路径
figure;
while iter <= iter_max
fprintf('迭代第%d次\n',iter);
% 随机产生各个蚂蚁的起点城市
start = zeros(m,1);
for i = 1:m
temp = randperm(n);
start(i) = temp(1);
end
Table(:,1) = start;
% 构建解空间
citys_index = 1:n;
% 逐个蚂蚁路径选择
for i = 1:m
% 逐个城市路径选择
for j = 2:n
tabu = Table(i,1:(j - 1)); % 已访问的城市集合(禁忌表)
allow_index = ~ismember(citys_index,tabu);
allow = citys_index(allow_index); % 待访问的城市集合
P = allow;
% 计算城市间转移概率
for k = 1:length(allow)
P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta;
end
P = P/sum(P);
% 轮盘赌法选择下一个访问城市
Pc = cumsum(P);
target_index = find(Pc >= rand);
target = allow(target_index(1));
Table(i,j) = target;
end
end
% 计算各个蚂蚁的路径距离
Length = zeros(m,1);
for i = 1:m
Route = Table(i,:);
for j = 1:(n - 1)
Length(i) = Length(i) + D(Route(j),Route(j + 1));
end
Length(i) = Length(i) + D(Route(n),Route(1));
end
% 计算最短路径距离及平均距离
if iter == 1
[min_Length,min_index] = min(Length);
Length_best(iter) = min_Length;
Length_ave(iter) = mean(Length);
Route_best(iter,:) = Table(min_index,:);
else
[min_Length,min_index] = min(Length);
Length_best(iter) = min(Length_best(iter - 1),min_Length);
Length_ave(iter) = mean(Length);
if Length_best(iter) == min_Length
Route_best(iter,:) = Table(min_index,:);
else
Route_best(iter,:) = Route_best((iter-1),:);
end
end
% 更新信息素
Delta_Tau = zeros(n,n);
% 逐个蚂蚁计算
for i = 1:m
% 逐个城市计算
for j = 1:(n - 1)
Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i);
end
Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i);
end
Tau = (1-rho) * Tau + Delta_Tau;
% 迭代次数加1,清空路径记录表
% figure;
%最佳路径的迭代变化过程
[Shortest_Length,index] = min(Length_best(1:iter));
Shortest_Route = Route_best(index,:);
plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...
[citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');
pause(0.3);
iter = iter + 1;
Table = zeros(m,n);
% end
end
%% 结果显示
[Shortest_Length,index] = min(Length_best);
Shortest_Route = Route_best(index,:);
disp(['最短距离:' num2str(Shortest_Length)]);
disp(['最短路径:' num2str([Shortest_Route Shortest_Route(1)])]);
%% 绘图
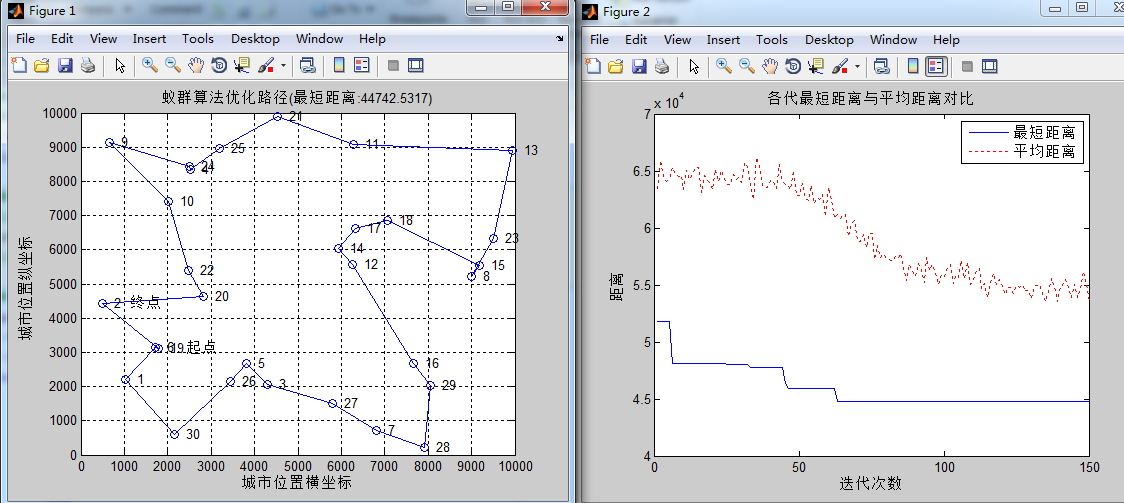
figure(1)
plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...
[citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');
grid on
for i = 1:size(citys,1)
text(citys(i,1),citys(i,2),[' ' num2str(i)]);
end
text(citys(Shortest_Route(1),1),citys(Shortest_Route(1),2),' 起点');
text(citys(Shortest_Route(end),1),citys(Shortest_Route(end),2),' 终点');
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
title(['蚁群算法优化路径(最短距离:' num2str(Shortest_Length) ')'])
figure(2)
plot(1:iter_max,Length_best,'b',1:iter_max,Length_ave,'r:')
legend('最短距离','平均距离')
xlabel('迭代次数')
ylabel('距离')
title('各代最短距离与平均距离对比')
三、使用该语句生成随机序列:


四、随机改变alpha、beta和rho参数:
初始数据:
(1)信息素重要程度因子:
将原来的alpha=1改为alpha=2结果。其余参数相同显示结果:


将原来的alpha=1改为alpha=4,其余参数相同显示结果:

(2) 启发函数重要程度因子:
将原来的beta=5改为beta=7,其余参数相同显示结果:

(2)信息素挥发因子:
将原rho=0.1改为rho=0.5,其他参数相同:

五、结果分析:
1、蚂蚁数量,迭代次数相同,rho=0.1与rho=0.5
将信息素调整为0.5,可以发现当信息素增大,虽然信息素的挥发速度越来越快,但是寻找到的最短路径反而比之前的更短,当rho过小 .时,未被选中的路径.上的信息素量将迅速衰减,容易陷入局部最优,算法的收敛性加大。另外,当rho过大时,被选中的路径上的信息素量增量减小,使搜索空间变大,这样算法虽然.陷入局部最优的可能性减小,但是算法的收敛性降低。因此经过调试,rho取[0.5,0.9]时, 较为合适。
2、蚂蚁数量,迭代次数,信息素相同,将信息素因素alpha=1与alpha=2、alpha=4
当alpha=1时,平均距离是以较为平缓的速度逐渐减少,将alpha=2, 在寻找各个城市的序列上并无差别,但最小距离增大,从图“各代最短距离与平均距离对比”中可以看出,当alpha=2时,在迭代次数大概为45- 55代中间,平均距离有急剧下降的现象而后逐渐趋于平缓,且各.代的最短距离在55代以内就已经趋于平缓。当alpha=4时,寻找到的城市序列出现了差别,此时起点是10,终点是7。迭代次数在40-55之间时,平均距离有急剧下降的现象而后逐渐趋于平缓,且各代的最短距离在30代以内就已经趋于平缓。且搜索到的最短距离也越来越大。,
Alpha的值越大,蚂蚁选择以前走过的路径的可能性就越大,局部最优路径上正反馈作用强,
搜索的随机性就减弱,算法会过早收敛。但当alpha值过小时,收敛速度慢,就容易使蚁群陷入局部最优。经过多次的调试,alpha的值在[1,3]最为合适。
3、Bete=3、bete=7
当其他因素不变,bete改为3时,发现最短路径变小,且城市序列的起点为2,终点为10,在各代的最短距离与平均距离的总体趋势与
bete=5差不多,在最短距离的迭代中,在大概10代的时候有一个急剧的减少。在bete=7, 迭代过程中,各代的最短距离在10代以内就已经趋于平缓,bete的值反映了启发式信息在指导蚂蚁搜索过程中的重要程度。Bete过小,蚁群陷入随机搜索,就很难找到最优解。Bete过大,蚂蚁在某个局部点上选择局部最短路径的可能性也就越大,但蚁群搜索最优路径的随机性就减弱,容易陷入局部最优,且算法的收敛性可能变差。在调试中发现,bete的值取[3,6]最合适。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号