【Luogu】P3384主席树模板（主席树查询K小数）

 YEAH！我也是一个AC主席树模板的人了！

   其实是个半吊子

   我将尽量详细的讲出我的想法。

   主席树太难，我们先搞普通线段树好了

   普通线段树怎么做？我的想法是查询K次最小值，每次查完把查的数改成INF，查完再改回来。。。

   MDZZ

   于是就有了主席树。

   先不考虑主席树，我们来考虑一个奇特的线段树。

   一般的线段树，数列位置是下标，而把数列维护值作为线段树中存的元素。

   那我们如果反过来，把数列元素当做线段树的下标。。。？？？

   比如说数列【4 2 3 1】

   如果线段树的下标是1、2、3、4.。。。。。？

   那　 在数据离散之后

   我们要查第K大的数是不是比较简单。。。

   NIUBI!

  主席树同理。主席树的每一个节点都是一颗线段树，也就是说对【1~n】的每个前缀建一棵线段树，线段树的每一个节点存前缀【1~i】中属于【L~R】的数有多少个。比如根节点是[1..n]，一共i个数，sum[root] = i；根节点的左儿子是[1..(L+R)/2]，若不大于(L+R)/2的数有x个，那么sum[root.left] = x）。若要查找[i..j]中第k大数时，设某结点x，那么x.sum[j] - x.sum[i - 1]就是[i..j]中在结点x内的数字总数。而对每一个前缀都建一棵树，会MLE，观察到每个[1..i]和[1..i-1]只有一条路是不一样的，那么其他的结点只要用回前一棵树的结点即可，时空复杂度为O(nlogn)。

   那主席树怎么做这道题呢？

   最一开始建一棵空的线段树，也就是最开始的主席树。设这第0棵线段树的根节点为rt[0],

然后一个个把原序列元素加到对应位置。

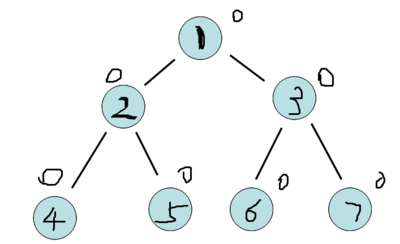
   比如我们刚举的那个例子，图片如下

       

   就像这样。观察到节点4、5、6、7对应原序列值域1~4。原序列前缀【1~0】中每个节点的值都是0.

   更新时可以发现只有一条路上的节点值有改变，于是新的线段树只需要自己新建logn个节点，其他的可以从旧线段树搬来：

   

   可以看到新的线段树使用了一部分旧线段树的节点，因为这些节点没有任何改动，新建太浪费空间时间。

   这样我们得到区间[l, r]的数要查询第k大便很容易了，设左节点中存的个数为cnt，当k<=cnt时，我们直接查询左儿子中第k小的数即可，如果k>cnt，我们只要去查右儿子中第k-cnt小的数即可，这边是一道很简单的线段树了。就如查找[1, 3]的第2小数，从根节点1向下搜，发现左儿子2的个数为1,1<2，所有去右儿子3中搜第2-1级第1小的数，然后再往下搜，发现左儿子6便可以了，此时已经搜到底端，所以直接返回节点6维护的值3即可就可以了。

   附上代码

#include<cstdio>
#include<cctype>
#include<cstring>
#include<algorithm>
#define mid ((l+r)>>1)
using namespace std;
inline long long read(){
    long long num=0,f=1;
    char ch=getchar();
    while(!isdigit(ch)){
        if(ch=='-')    f=-1;
        ch=getchar();
    }
    while(isdigit(ch)){
        num=num*10+ch-'0';
        ch=getchar();
    }
    return num*f;
}

long long *que;
long long *f;
long long *rt;
long long *ls;
long long *rs;
long long *sum;
long long tot;
long long *d;
void build(long long int &o,int l,int r){
    o=++tot;
    sum[o]=0;
    if(l==r)    return;
    build(ls[o],l,mid);
    build(rs[o],mid+1,r);
}

void update(long long &o,int l,int r,int last,long long p){
    o=++tot;
    ls[o]=ls[last];
    rs[o]=rs[last];
    sum[o]=sum[last]+1;
    if(l==r)    return;
    if(p<=mid)    update(ls[o],l,mid,ls[last],p);
    else         update(rs[o],mid+1,r,rs[last],p);
}

long long query(int from,int to,int l,int r,long long k){
    if(l==r)    return l;
    long long cnt=sum[ls[to]]-sum[ls[from]];
    if(k<=cnt)    return query(ls[from],ls[to],l,mid,k);
    else         return query(rs[from],rs[to],mid+1,r,k-cnt);
}

struct Que{
    int ID,tme;
    bool operator <(const Que &a)const{
        return tme<a.tme;
    }
}e[500000];
int Ans[500000][2];

int cc=1;
int ss;
int main(){
    int m=read(),n=read();
    que=new long long[m+10];
    f=new long long[m+10];
    rt=new long long [m*20];
    ls=new long long [m*20];
    rs=new long long [m*20];
    sum=new long long [m*20];
    d=new long long [m*20];
    for(int i=1;i<=m;++i){
        que[i]=read();
        f[i]=d[i]=que[i];
    }
    sort(f+1,f+n+1);
    int size=unique(f+1,f+n+1)-(f+1);
    build(rt[0],1,size);
    for(int i=1;i<=m;++i)    que[i]=lower_bound(f+1,f+size+1,que[i])-f;
    for(int i=1;i<=n;++i)    e[i]=(Que){i,read()};
    sort(e+1,e+n+1);
    for(int i=1;i<=n;++i){
        int tme=e[i].tme,ID=e[i].ID;
        while(cc<=tme){
            update(rt[cc],1,size,rt[cc-1],que[cc]);
            cc++;
        }
        int ans=query(rt[0],rt[tme],1,size,++ss);
        Ans[ID][1]=f[ans];
        Ans[ID][0]=1;
    }
    for(int i=1;i<=n;++i)
        if(Ans[i][0])
            printf("%d\n",Ans[i][1]);
    return 0;
}