大数据笔记-外存算法
4.1外存存储结构与外存算法:
分层存储:
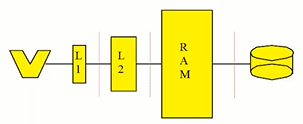


做法:

可扩展性问题:若程序分散地访问磁盘上的数据,即使是好的操作系统也无法利用数据块存取优势
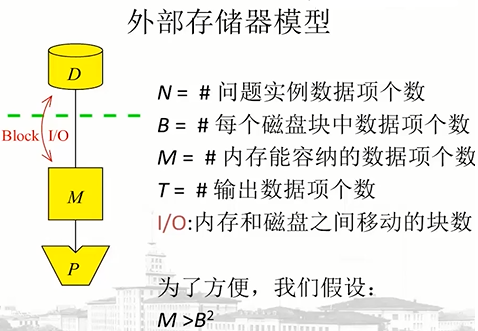
基本界限:
 、
、
队列和堆栈:
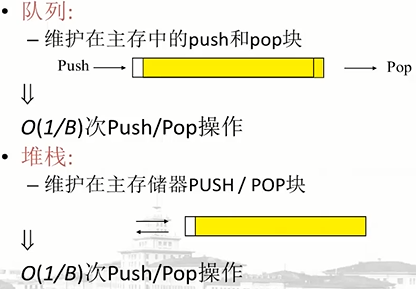
4.2外存算法示例:外存排序算法
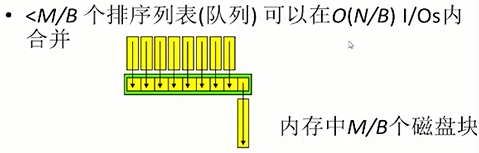
算法的分析1:(多路归并)
M/B路
以块为单位进行调度
1.首先从磁盘里把磁盘块放进内存,在内存中进行排序,每次放M/B块,一共放N/B块。做完后,外存中已经是在大小为M/B的区域里、分别排好序的数据。再分别取M/B-1个这些区域的第一个元素,放入内存中。
2.在内存中,将M/B-1块用于磁盘块的归并,剩余的一块用作缓存
do{
step1.[取出]M/B-1块中最小的数据,放于缓存中
step2.(用于缓存的磁盘块未满,step1)||(缓存满后,写出到外存,清空缓存)||(前M/B-1个磁盘块中的数据被取完,加载相应区域的下一个磁盘块)
}while(将所有的磁盘块中的数据都进行了排序)
疑问:如果step1中,排序磁盘块的次数大于M/B-1,那么归并排序时应该怎么做?
(演示的例子里,在内存中排序磁盘块的次数=M/B-1=3)
循环停止条件:(k-1代表第k轮)
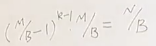

算法分析2:(快排)
根号(M/B)路

M=8,N=24,B=2
(8,16是选择的分点,buffer磁盘块的大小为B,buffer满了以后,将里面的数据写到外存)

此时,写出到外存的三个区域的元素还没进行排序,但是大小已经可以放进内存,接下来将数据放进内存进行排序。若大小仍不能放进内存,则继续上述做法,直到数据块的大小可以放进内存。
复杂度分析:
划分停止条件:
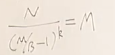
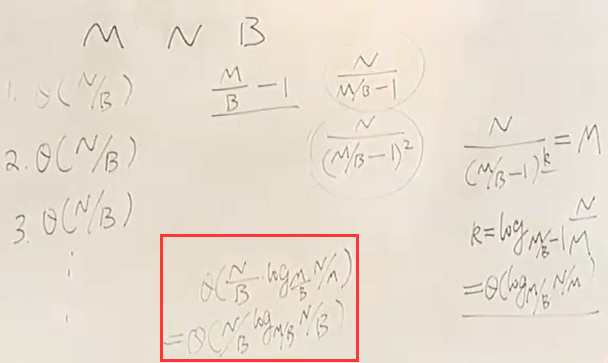
计算分割元素:

存在的问题: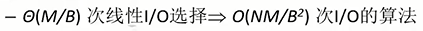
解决方法:

改进的算法的步骤:


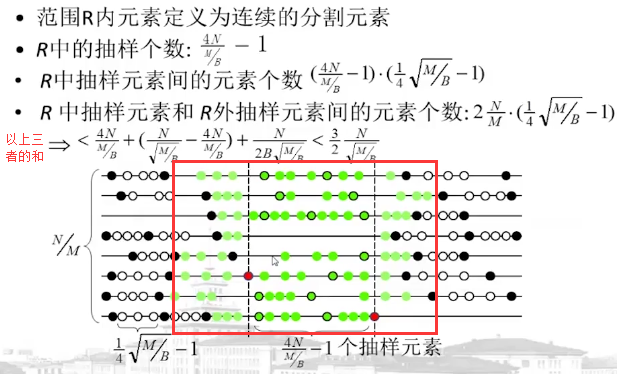
从而得到每一路归并的元素上限。
算法复杂性分析:

其中,步骤二经过根号(M/B)次抽取分割元素,在4N/根号(M/B)的数据(第一次的抽样的结果)内抽取
总结:

它们都是最优的。
4.3外存数据结构示例:外存查找树
内存查找树:
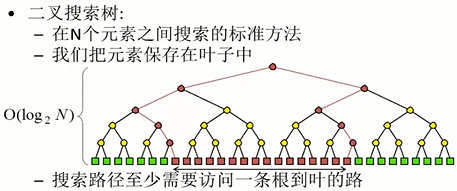
外存查找树:
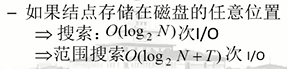
外部搜索树:
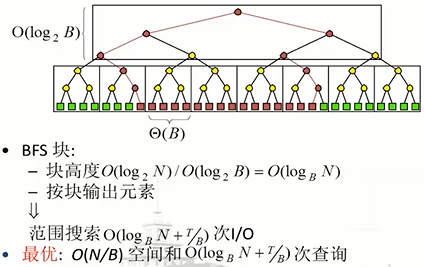
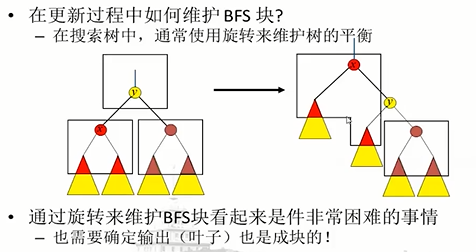
存在的问题:使用红黑树维护BFS块
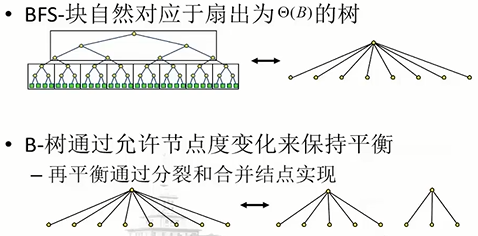
5.1B树:
B树上的查询:
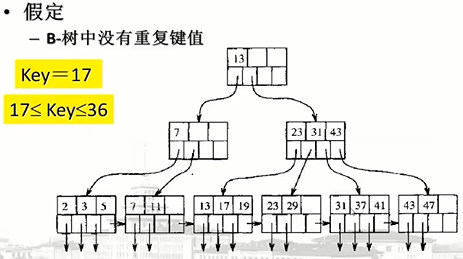
为符合需求,B树应该满足的性质:
(a,b)树:

“所有的叶子在同一层并且包括a到b个元素”:叶子节点的磁盘块的数量为[a,b]
对(a,b)树进行分析:

(a,b)树中的操作:
插入:

删除:

注:若最后合并影响了根节点,使根节点的儿子小于a,此时根节点是不变的(参考上文对根节点数量的定义)。然而,若根节点只有一个儿子,则把根节点给删了
B树的结论:

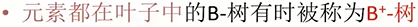

5.2KD树


查询:
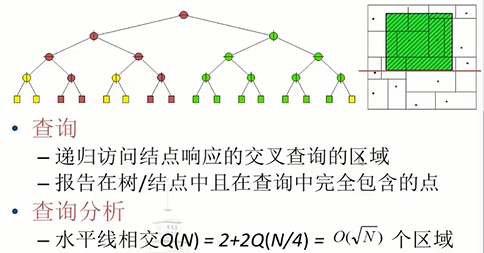
kdB-树:

kdB-树的构建:

改进:
![]()

复杂度:
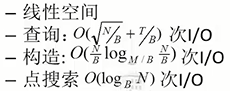
动态地改进:
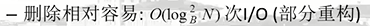
插入:
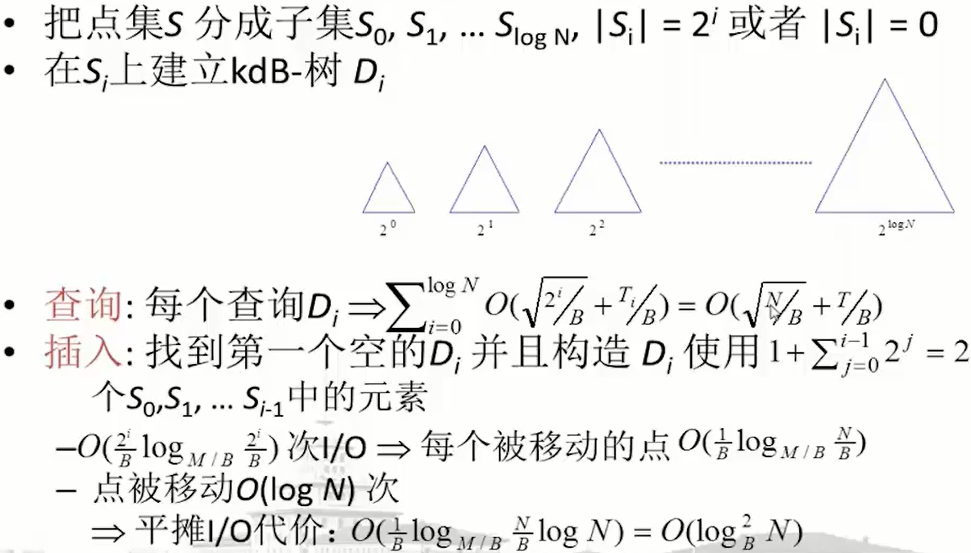
删除:

kdB-树总结:

6.1 表排序及其应用
表排序(List Ranking)
表排序的困难之处:
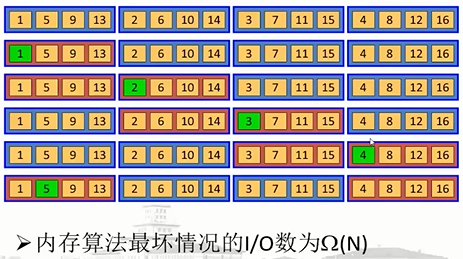
一种高效的表排序算法:
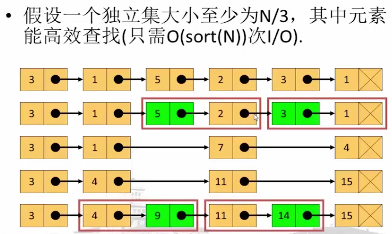
分析:

目标:对给定的树T,以表L表示,进而让对T的每一种计算可用对L的一种rank来完成
欧拉回路技术:
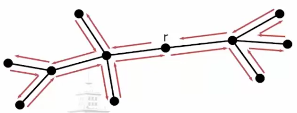
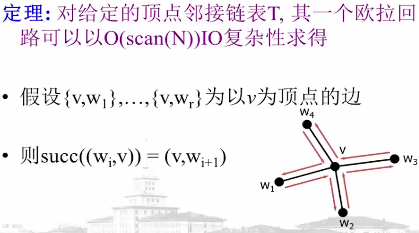
应用场景:
1.父子关系判定:

2.计算前序计数:
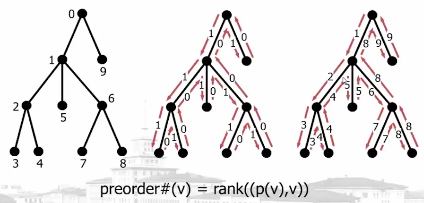
3.计算子树大小:
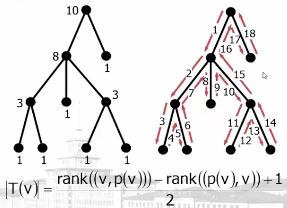
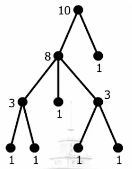
6.2时间前向处理方法:
将图问题表示为有向无环图的估值问题

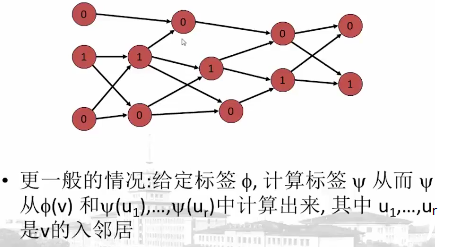
处理过程:

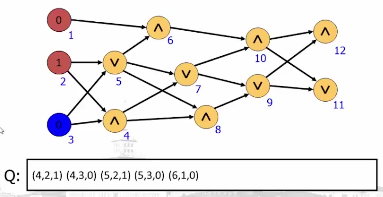
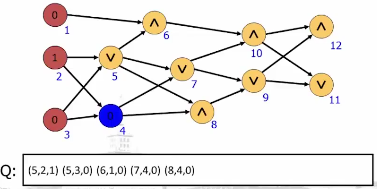
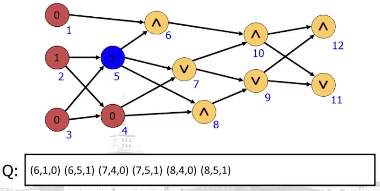
......

测试:
求最大独立集MIS(贪心法,不一定求得最优解):

(1的入度为0,在I中,选取后面的节点时,若其父亲节点在I中,则该节点不能加入I中):


6.3缩图法:

即把大的图缩到内存中
求连通性->半外存算法:结点在内存中,边在外存中
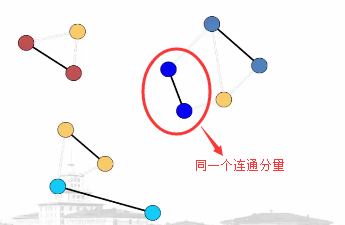
算法分析:

M(memory)
若|V|>M:

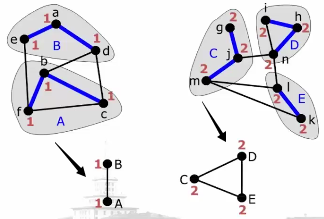

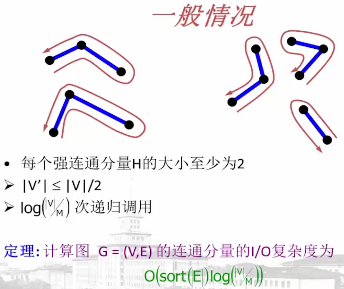
算法复杂度分析:
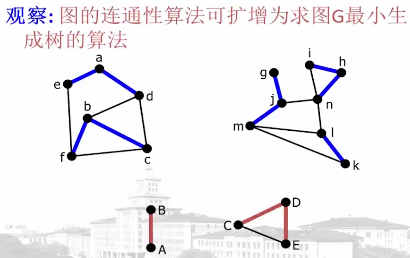
应用:最小生成树
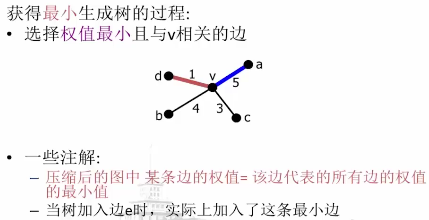
时间复杂度分析:
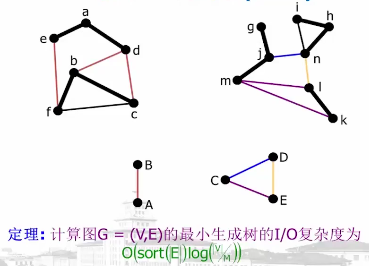
另一种图算法技术:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号