Fama-French三因子模型

Fama-French三因子模型理论知识

模型介绍

Fama和French 1992年对美国股票市场决定不同股票回报率差异的因素的研究发现，股票的市场的beta值不能解释不同股票回报率的差异，而上市公司的市值、账面市值比、市盈率可以解释股票回报率的差异。Fama and French认为，上述超额收益是对CAPM 中β未能反映的风险因素的补偿。

模型表达式为：

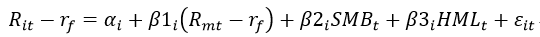
其中Rit代表资产收益率，rf代表无风险收益率；Rit-rf为超额市场收益率；SMBt代表市值规模因子，HMLt代表账面市值比因子，β1i、β2i、β3i分别为Rit-rf、SMBt、HMLt的系数，εit为残差项，αi为截距项。

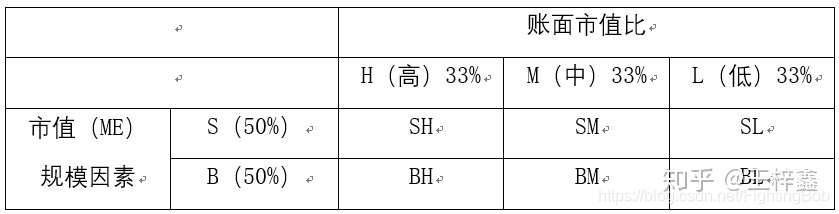
三因子构建方法

首先先根据上市公司的市值，按照其大小值进行排序并分为两组，记为S、B，S、B分别表示为小市场规模股和大市场规模股。然后再根据年末上市公司账面市值比，按照33%、33%、33%的比例排序，记为L、M、H，L、M、H分别为低价值、中等价值、高价值；最后即可得到股票交叉组合，并通过加权平均（以总市值为权重）计算它们的月收益率{SL,SM,SH,BL,BM,BH}。

通过以上6个组合的月收益率数据即可构造出市值规模因子（SMB），具体计算公式如下：

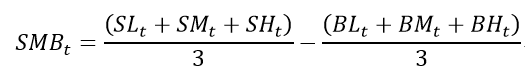
通过该方法得到的市值规模因子体现出市值规模小的投资组合与市值规模大的投资组合之间的收益率差异，剔除账面市值比因素所造成的影响。

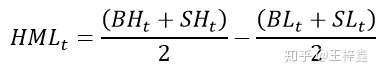
同理，得到账面市值比因子也保证了解释变量只考虑账面市值比所产生的影响，反映账面市值比高的投资组合与账面市值比低的投资组合之间的收益率差异。

理论假设

在探讨Fama—French三因子模型的应用时，是以“有限理性”理论假设为基础。并在此基础上得出若干基本假定： 　　(1)存在着大量投资者； 　　(2)所有投资者都在同一证券持有期计划自己的投资资产组合； 　　(3)投资者投资范围仅限于公开金融市场上交易的资产； 　　(4)不存在证券交易费用(佣金和服务费用等)及税赋； 　　(5)投资者们对于证券回报率的均值、方差及协方差具有相同的期望值； 　　(6)所有投资者对证券的评价和经济局势的看法都一致。

统计假设

从模型的表达式可以看出，FF模型属于多元回归模型。其基本假设为： 　　(1)(Rm − Rf)、SMB、HML与随机误差项u不相关； 　　(2)零均值假定：E(εi)=0； 　　(3)同方差假定，即 的方差为一常量：Var(εi)=S^2； 　　(4)无自相关假定：cov(εi,εj)=0,i≠j； 　　(5)解释变量之间不存在线性相关关系。即两个解释变量之间无确切的线性关系； 　　(6)假定随机误差项 服从均值为零，方差为S2正态分布，即εi~N(0,S^2)。

Python实现

本次案例数据来自锐思数据库，选取2019年创业板所有股票作为样本。

第一部分：导入数据

import pandas as pd
data = pd.read_csv('F:\\python\\【案例】数据分析)

第二部分：计算三因子

首先，我们需要计算每一天的三因子，在此之前我们就需要提取每个交易日日期。 读取数据中的‘date’列，并去重：

date = data['date']
date.drop_duplicates(keep='first',inplace=True)

参数说明： data.drop_duplicates(subset=['A','B'],keep='first',inplace=True) 1、代码中subset对应的值是列名，表示只考虑这两列，将这两列对应值相同的行进行去重。默认值为subset=None表示考虑所有列； 2、keep='first'表示保留第一次出现的重复行，是默认值。keep另外两个取值为"last"和False，分别表示保留最后一次出现的重复行和去除所有重复行； 3、inplace=True表示直接在原来的DataFrame上删除重复项，而默认值False表示生成一个副本。

接下来我们利用循环语句依次提取每一天中所有股票数据，并进行计算（这里以‘2019/1/3’为例，循环代码就不在此展示，可在完整代码中查看） 提取‘2019/1/3’的数据，即data1：

data = data.reset_index(drop=True)
data1 = data[data['date'] == date[1]]

 

 

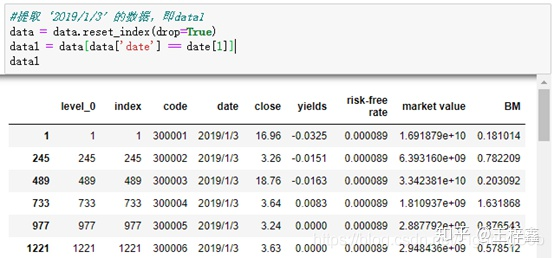
说明： 在循环语句中.reset_index(drop=True) 这句代码，必须要加drop=True，否则会报错。因为在.reset_index()重置索引时，会插入列'index'或'level_0'，如果它们之一/(两者都已经被占用),那么它会报错。所以需要使用“drop”选项，这将删除具有相同名称的现有索引,并使用新的重置索引替换它。 疑问： 这两句代码中，如果没有‘data = data.reset_index(drop=True)’这句代码，那么第二句代码便会报错，并不知道具体理由，还望大神指点！

紧接着，我们依次按照市值和账面市值比进行排序，先按照市值分为大小两组，再在每组中按照账面市值比分为高中低三组。 按市值排序，即data2：

data2 = data1.sort_values('market value')

参数说明： sort_values(by=’’,axis=0,ascending=False)#排序 1、by是指定需要排序的列的标签名； 2、axis为需要排序的轴，0代表行，1代表列； 3、ascending表示排序方法，True表示升序，False表示降序。

按市值分组，并按账面市值比进行升序排序：

data2_big = data2[0:round(len(data2)/2)].sort_values(by='BM',axis=0,ascending=True)
data2_small = data2[round(len(data2)/2):len(data2)].sort_values(by='BM',axis=0,ascending=True)

按账面市值比分组：

data2_big_low = data2_big[0:round(len(data2_big)/6)]
data2_big_medium = data2_big[round(len(data2_big)/6):round(len(data2_big)/3)]
data2_big_high = data2_big[round(len(data2_big)/3):len(data2_big)]
data2_small_low = data2_small[0:round(len(data2_small)/6)]
data2_small_medium = data2_small[round(len(data2_small)/6):round(len(data2_small)/3)]
data2_small_high = data2_small[round(len(data2_small)/3):len(data2_small)]

计算三因子：

R_market = sum(data1['yields']*data1['market value'])/sum(data1['market value'])
SL = sum(data2_small_low['yields']*data2_small_low['market value'])/sum(data2_small_low['market value'])
SM = sum(data2_small_medium['yields']*data2_small_medium['market value'])/sum(data2_small_medium['market value'])
SH = sum(data2_small_high['yields']*data2_small_high['market value'])/sum(data2_small_high['market value'])
BL = sum(data2_big_low['yields']*data2_big_low['market value'])/sum(data2_big_low['market value'])
BM = sum(data2_big_medium['yields']*data2_big_medium['market value'])/sum(data2_big_medium['market value'])
BH = sum(data2_big_high['yields']*data2_big_high['market value'])/sum(data2_big_high['market value'])
SMB = (SL+SM+SH)/3-(BL+BM+BH)/3
HML = (BH+SH)/2-(BL+SL)/2

最后我们创建一个用于存放三因子的数组‘TF’，将计算出来的每日三因子存放进去：

TF = pd.DataFrame(columns=['date','R_market','SMB','HML'])
new = pd.DataFrame([[date[1],R_market,SMB,HML]],columns=['date','R_market','SMB','HML'])
TF = TF.append(new,ignore_index=True)

 

 

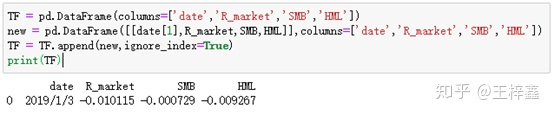
疑问： 看过我之前文章的小伙伴一定发现，在之前文章中使用.append()并没有赋值，但在此次案例中，如果没有赋值将会出错，这一点仍存有疑惑。

将上述步骤用循环语句整合在一起便可计算出每一天的三因子，在这里就不进行代码展示，大家可在完整代码中查看。

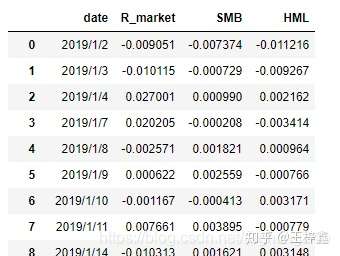
我们根据Fama-French三因子模型，整理出我们所需的自变量和因变量。 整理回归数据：

TF_hg = pd.DataFrame(columns=['date','R_market','SMB','HML'])
for code_date in code['date']:
    choose = TF[TF['date']==code_date]
    TF_hg = TF_hg.append(choose,ignore_index=True)
TF_hg['return']=code['yields']-code['risk-free rate']

 

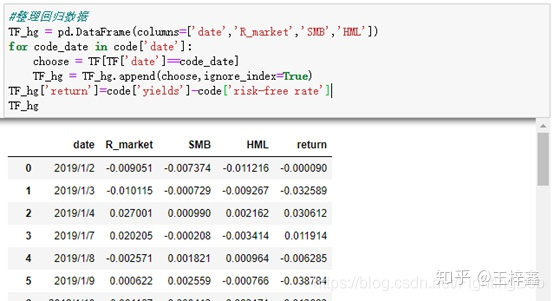
 紧接着，我们就可以导入所需的库进行回归了：

import numpy as np
import statsmodels.api as sm

最后，我们分别将自变量和因变量赋值给x，y后，进行建模：

x = np.column_stack((TF_hg['R_market'], TF_hg['SMB'], TF_hg['HML']))
y = TF_hg['return']
X = sm.add_constant(x)
model = sm.OLS(y, X).fit()
print(model.summary())

 

 

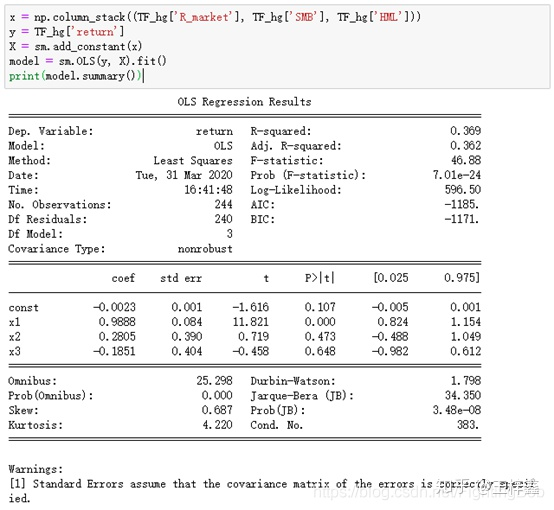
说明： 1、在.OLS()的参数中，数据的类型要求为‘numpy.ndarray’，所以需要加载numpy库，我们之前的数组都是‘DataFrame’，无法直接使用； 2、.fit()是将模型中所有参数进行整理，如果不加这句，summary()、params()便无法调用。

最后再给大家介绍两个常用函数——summary()、params()，以便提取所需内容。 summary()是概括模型信息，上图以进行展示； params()是自变量系数：

model.params['x1']