机器学习中的核函数与核方法

一、什么是“核函数”

我们都知道，机器学习（神经网络）的一个很重要的目的，就是将数据分类。我们想象下面这个数据（图1），在二维空间（特征表示为和）中随机分布的两类数据（用圆圈和叉叉表示）。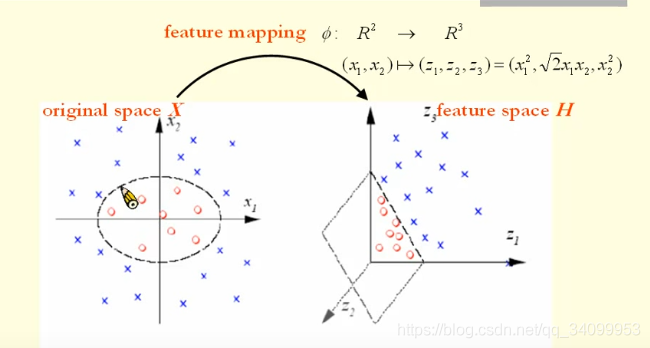

 


如果我们想要将这两类数据进行分类，那么分类的边界将会是一个椭圆: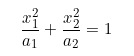

但是如果我们可以通过一个映射，将数据的特征通过某个非线性映射映射到三维空间，其特征表示为，并且映射关系为那么我们是不是就可以用一个平面来将其分类，也即是将上述椭圆的x特征换成z特征：

其实这个映射，就是将一个空间中的特征转换到另外一个空间，这就是空间转换（映射）的意义，即可以将原来线性不好分的数据转换到另外一个空间，在这个空间中可以用一个超平面线性可分。
在机器学习中，我们要用到内积运算。而在映射后的高维空间中，内积往往是很不好求解的。所以，我们能不能找到在低维空间中的某个运算，恰好等于高维空间中的内积运算呢？

 

 
设在原空间中有两个点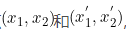，映射到高维空间中变成

 

 
我们就将低维空间中的这个对于内积的运算定义为核函数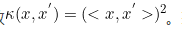换句话说，核函数就是低维空间中的内积的某个函数

 

 因为在别的例子中，有可能不是内积的平方。即核函数就等于就是高维空间的内积。

 

 Kernel methods can be thought of as instance-based learners: rather than learning some fixed set of parameters corresponding to the features of their inputs, they instead "remember" the i-th training example (xi, yi) and learn for it a corresponding weight wi.
二、为什么要用核函数

因为在机器学习中，我们求解的过程要用到内积，而变换后的高维空间的内积我们不好求，所以我们定义了这个核函数，可以把高维空间的内积运算转化成内为空间的某些运算，这样求起来不是很简单吗？
换句话说，如果我们有了核函数，我们就不再需要知道那个映射到底是个什么鬼，我们就可以直接通过核函数，就可以求导高维空间的内积了，从而可以计算出高维空间中两个数据点之间的距离和角度。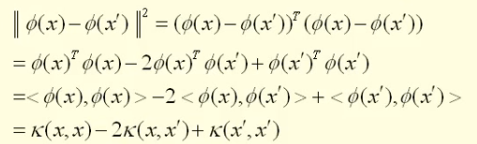

 

 

 

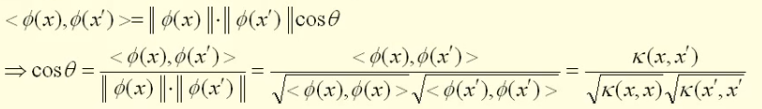
 三、怎么用？（一个简单的分类例子）

现在我们假设，有N个数据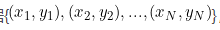，其中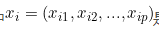 是第i个数据的p维特征，是第i个数据的分类标签,现将其映射到高维空间变成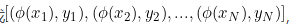而在这个空间中，有两个类别，所以标签可以假定为+和-，其中每一类的样本个数为n。正样本的中心点负样本的中心点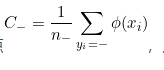从C-到C+有一条差向量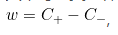而w的中心点为C，所以在C点垂直于w的超平面就是两类的分类边界。

 

 

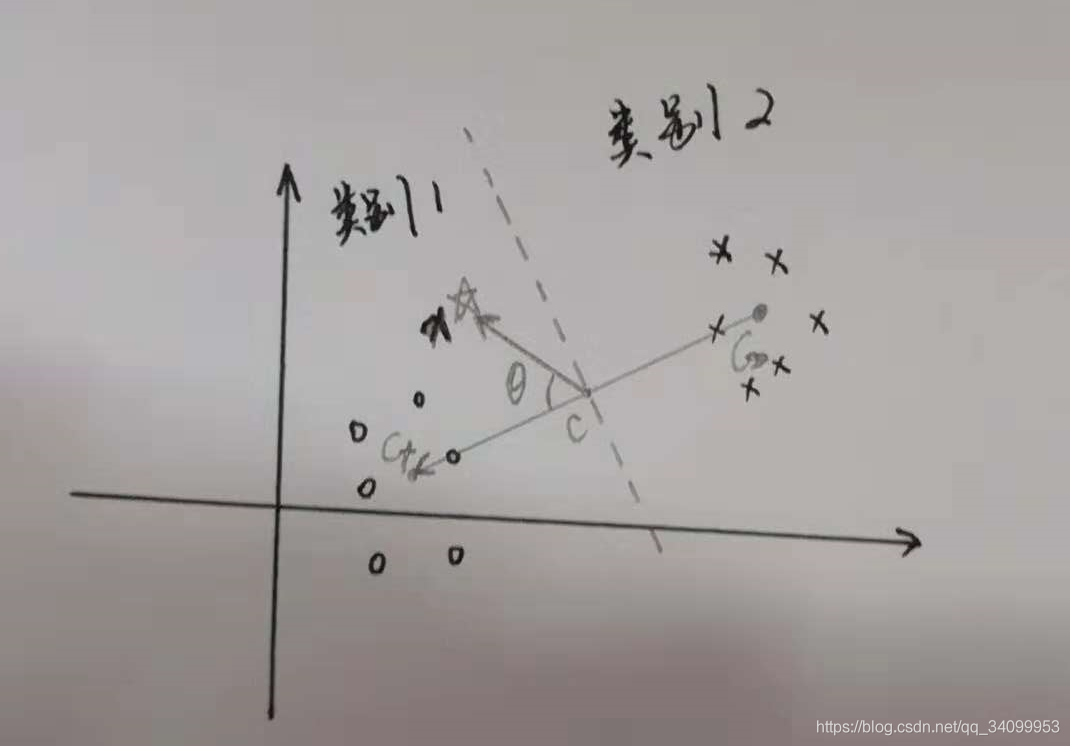
而想要把某个数据\small \phi(x)分类为+的依据为：从C点到样本点的向量差与w向量的夹角应该小于90°，也即:\small 0<cos\theta<1；反之，\small \small 0>cos\theta>-1。即，当内积为正，那就说明在分类1，内积为负，就说明在分类2。即：

\small y=sgn(<\phi(x)-C,w>)=sgn(w^{T}\phi(x)-w^{T}C)

于是我们来\small cos\theta的表达式：

\small cos\theta=\frac{<\phi(x)-C,w>}{|\phi(x)-C||w|} =\frac{1}{a}<\phi(x)-C,w>= \frac{1}{a}(<\phi(x),w>-<C,w>)

(PS:说到这，你应该知道为什么分类需要内积了吧？因为内积的正负代表了数据点是位于分类边界的正方向还是负方向，从而实现分类。)

其中:

后面的就不继续写了，化简形式都一样，即：我们就可以把高维空间的内积，改写成低维空间的核函数的形式，这样在不知道映射是个什么鬼的情况下吗，也可以轻松地进行分类工作了。

四、补充一点

1. 有限半正半定：给定任意有限 n个点（x1~xn）,求解其矩阵是正定的：

\small \kappa =\begin{bmatrix} \kappa(x_1,x_1) & ... &\kappa(x_1.x_n) \\ ...& ... & ...\\ \kappa(x_n,x_1)&... & \kappa(x_n,x_n) \end{bmatrix} \geq 0

 

正定核函数还有另外一个定义：

如果核函数满足以下两条性质：
①对称性
②正定性
则称核函数K(x,z)为正定核函数。

这个定义也就是正定核函数的充要条件，其中两条性质分别指的是：

①对称性\Leftrightarrow K(x,z)=K(z,x);
②正定性\Leftrightarrow任取N个元素x_{1},x_{2},\cdots ,x_{N}\in \mathcal{X},对应的Gram\; matrix\; K=[K(x_{i},x_{j})]是半正定的。

证明K(x,z)=\phi (x)^{T}\phi (z)\Leftrightarrow对称性+矩阵K半正定：

①\Rightarrow:
首先证明对称性

K(x,z)=<\phi (x),\phi (z)>\\ K(z,x)=<\phi (z),\phi (x)>\\ 又内积具有对称性，即<\phi (x),\phi (z)>=<\phi (z),\phi (x)>\\ \therefore K(x,z)=K(z,x)\\ \therefore K(x,z)满足对称性

然后证明

欲证Gram\; matrix:K=[K(x_{i},x_{j})]_{N\times N}半正定\\ 即证：\forall \alpha \in \mathbb{R}^{n},\alpha ^{T}K\alpha \geq 0\\ \because \alpha ^{T}K=\begin{pmatrix} \alpha _{1} & \alpha _{2} & \cdots & \alpha _{N} \end{pmatrix}_{1\times N}\begin{bmatrix} a_{11}& a_{12}& \cdots & a_{1N}\\ a_{21}& a_{22}& \cdots & a_{2N}\\ \vdots & \vdots & \ddots & \vdots \\ a_{N1}& a_{N2}& \cdots & a_{NN} \end{bmatrix}_{N\times N}\begin{pmatrix} \alpha _{1}\\ \alpha _{2}\\ \vdots \\ \alpha _{N} \end{pmatrix}_{N\times 1}\\ =\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha _{i}\alpha _{j}K_{ij}\\ =\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha _{i}\alpha _{j}<\phi (x_{i}),\phi (x_{j})>\\ =\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha _{i}\alpha _{j}\phi (x_{i})^{T}\phi (x_{j})\\ =\sum_{i=1}^{N}\alpha _{i}\phi (x_{i})^{T}\sum_{j=1}^{N}\alpha _{j}\phi (x_{j})\\ =\begin{bmatrix} \sum_{i=1}^{N}\alpha _{i}\phi (x_{i})\end{bmatrix}^{T}\sum_{j=1}^{N}\alpha _{j}\phi (x_{j})\\ =<\sum_{i=1}^{N}\alpha _{i}\phi (x_{i}),\sum_{j=1}^{N}\alpha _{j}\phi (x_{j})>\\ =\left \|\sum_{i=1}^{N}\alpha _{i}\phi (x_{i}) \right \|^{2}\geq 0\\ \therefore K是半正定的。

②\Leftarrow:

\;对K进⾏特征分解，对于对称矩阵K=V\Lambda V^{T}，那么令\phi (x_{i})=\sqrt{\lambda _{i}}V_{i}，\\其中V_{i}是特征 向量，于是就构造了K(x,z)=\sqrt{\lambda _{i}\lambda _{j}}V_{i}^{T}V_{j}。

得证。

说明一下证明矩阵半正定的两种方法：

①特征值\geq 0
②\forall \alpha \in \mathbb{R}^{n},\alpha ^{T}A\alpha \geq 0



posted @ 2021-07-30 15:17  celine227  阅读(788)  评论(0)  编辑  收藏  举报