模式识别与机器学习中数学推导中用到的数学知识
每次手推公式就会遇见各种不会的，在网上搜了个总结的还不错的常用求导公式。。。继续更新中……
一、基本线性代数
以下部分原文地址：http://blog.163.com/live_freely/blog/static/151142060201023154057339/
在网上看到有人贴了如下求导公式：
Y = A * X --> DY/DX = A'
Y = X * A --> DY/DX = A
Y = A' * X * B --> DY/DX = A * B'
Y = A' * X' * B --> DY/DX = B * A'
于是把以前学过的矩阵求导部分整理一下：
1. 矩阵Y对标量x求导：
相当于每个元素求导数后转置一下，注意M×N矩阵求导后变成N×M了
Y = [y(ij)] --> dY/dx = [dy(ji)/dx]
2. 标量y对列向量X求导：
注意与上面不同，这次括号内是求偏导，不转置，对N×1向量求导后还是N×1向量
y = f(x1,x2,..,xn) --> dy/dX = (Dy/Dx1,Dy/Dx2,..,Dy/Dxn)'
3. 行向量Y'对列向量X求导：
注意1×M向量对N×1向量求导后是N×M矩阵。
将Y的每一列对X求偏导，将各列构成一个矩阵。
重要结论：
dX'/dX = I
d(AX)'/dX = A'
4. 列向量Y对行向量X’求导：
转化为行向量Y’对列向量X的导数，然后转置。
注意M×1向量对1×N向量求导结果为M×N矩阵。
dY/dX' = (dY'/dX)'
5. 向量积对列向量X求导运算法则：
注意与标量求导有点不同。
d(UV')/dX = (dU/dX)V' + U(dV'/dX)
d(U'V)/dX = (dU'/dX)V + (dV'/dX)U'
重要结论：
d(X'A)/dX = (dX'/dX)A + (dA/dX)X' = IA + 0X' = A
d(AX)/dX' = (d(X'A')/dX)' = (A')' = A
d(X'AX)/dX = (dX'/dX)AX + (d(AX)'/dX)X = AX + A'X
6. 矩阵Y对列向量X求导：
将Y对X的每一个分量求偏导，构成一个超向量。
注意该向量的每一个元素都是一个矩阵。
7. 矩阵积对列向量求导法则：
d(uV)/dX = (du/dX)V + u(dV/dX)
d(UV)/dX = (dU/dX)V + U(dV/dX)
重要结论：
d(X'A)/dX = (dX'/dX)A + X'(dA/dX) = IA + X'0 = A
8. 标量y对矩阵X的导数：
类似标量y对列向量X的导数，
把y对每个X的元素求偏导，不用转置。
dy/dX = [ Dy/Dx(ij) ]
重要结论：
y = U'XV = ΣΣu(i)x(ij)v(j) 于是 dy/dX = = UV'
y = U'X'XU 则 dy/dX = 2XUU'
y = (XU-V)'(XU-V) 则 dy/dX = d(U'X'XU - 2V'XU + V'V)/dX = 2XUU' - 2VU' + 0 = 2(XU-V)U'
9. 矩阵Y对矩阵X的导数：
将Y的每个元素对X求导，然后排在一起形成超级矩阵。
二、具体内容
1. hessian 矩阵，有函数
则其hessian举证H(f)为
hessian矩阵可以判断函数的凹凸性，以及函数的极值点问题
当函数
二阶连续可导时，Hessian矩阵H在临界点
上是一个
阶的对称矩阵。
- 当H是正定矩阵时，临界点是一个局部的极小值，f是下凸函数。
- 当H是负定矩阵时，临界点是一个局部的极大值，f是上凸函数。
- H=0,需要更高阶的导数来帮助判断。
- 在其余情况下，临界点不是局部极值
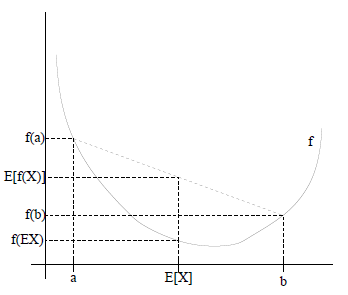
2. Jensen不等式
如果f是凸函数，X是随机变量，那么 
特别地，如果f是严格凸函数，那么
当且仅当
，也就是说X是常量。
这里我们将
简写为
。
如果用图表示会很清晰：
