[POI2014]HOT-Hotels加强版
这是个长剖练习题。但是重点在于dp。
数据范围达到\(10^5\),所以直接dp是不可取的。
设\(f_{x,i}\)表示\(x\)子树内有多少个点距离\(x\)为i。
显然有转移方程\(f_{x,i}+=f_{y,i-1}\)
根据题设,假设一个节点为\(t\),则题目要求\(dis(x,t)=dis(y,t)=dis(z,t)\)的三元组\(x,y,z\)的个数。
由于枚举其他元素都不太行,所以考虑枚举\(t\)。则三元组的形式肯定是两个点在\(z\)的子树,一个点从\(z\)上面伸出一个距离\(k\)到节点\(b\),在\(b\)的一个不包含\(t\)的子树内伸出\(d-k\)。
当\(k=0\),则三元组\(x,y,z\)都在\(t\)的子树内。
设\(g_{x,i}\)表示\(x\)节点子树中有多少个点对的lca到\(x\)的距离为\(d-i\)。
转移有:两个儿子在同一个儿子的子树中,在不同儿子的子树中。
第一个转移:\(g_{x,i}+=g_{y,i+1}\)。
第二个转移:\(g_{x,i}+=f_{y,i-1}*f_{z,i-1}\),其中\(y,z\)分属\(x\)的不同子树。
统计答案时,统计三个点都在当前点的子树内,或者一个点伸出当前子树,并且在\(x\)的子树内。
第一个贡献是\(g_{x,0}\)。
第二个贡献为\(f_{x,j-1}*g_{y,j+1}\),其中\(y,z\)分属\(x\)的不同子树。
这部分是统计以x为三个点的lca的答案。
如下图:
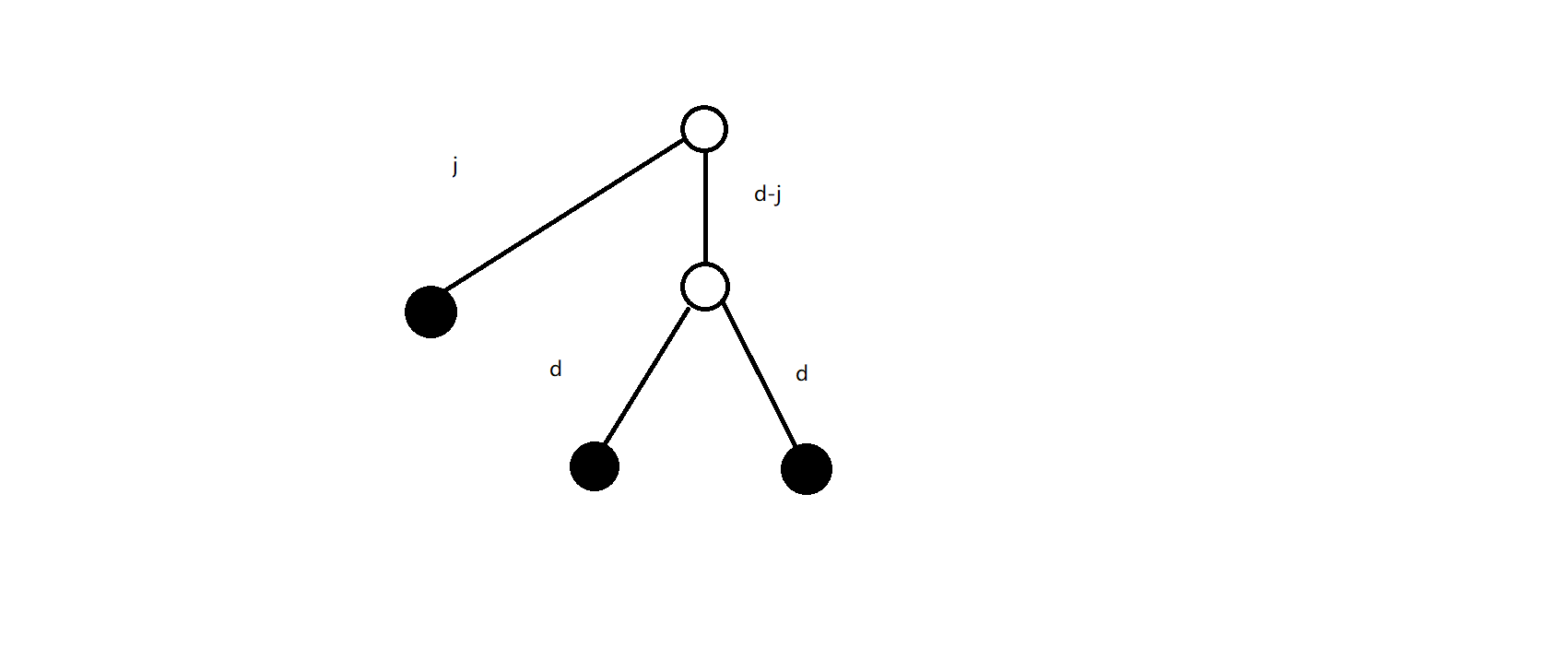
对每个节点都做一次这个dp。
直接做是\(O(n^2)\)的。但是可以长短链剖分,时间复杂度降到\(O(n)\)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号