上篇中,我们了解到HMM的相关知识,并且知道HMM属于概率有向图模型,接下来,让我们一起学习总结概率无向图模型——条件随机场(Conditional Random Field, CRF)。
思维导图
![]()
概率无向图模型
概率无向图模型又称为马尔可夫随机场,是一个可以由无向图表示的联合概率分布。
模型定义
\[设有联合概率分布P(Y),由无向图G=(V,E)表示,V表示结点集合,E表示边集合,\\在图G中,结点表示随机变量,边表示随机变量之间的依赖关系。如果联合概率分布P(Y)满足\\成对、局部或全局马尔可夫性,就称此联合概率分布为概率无向图模型或马尔可夫随机场。
\]
![]()
马尔可夫性
成对马尔可夫性
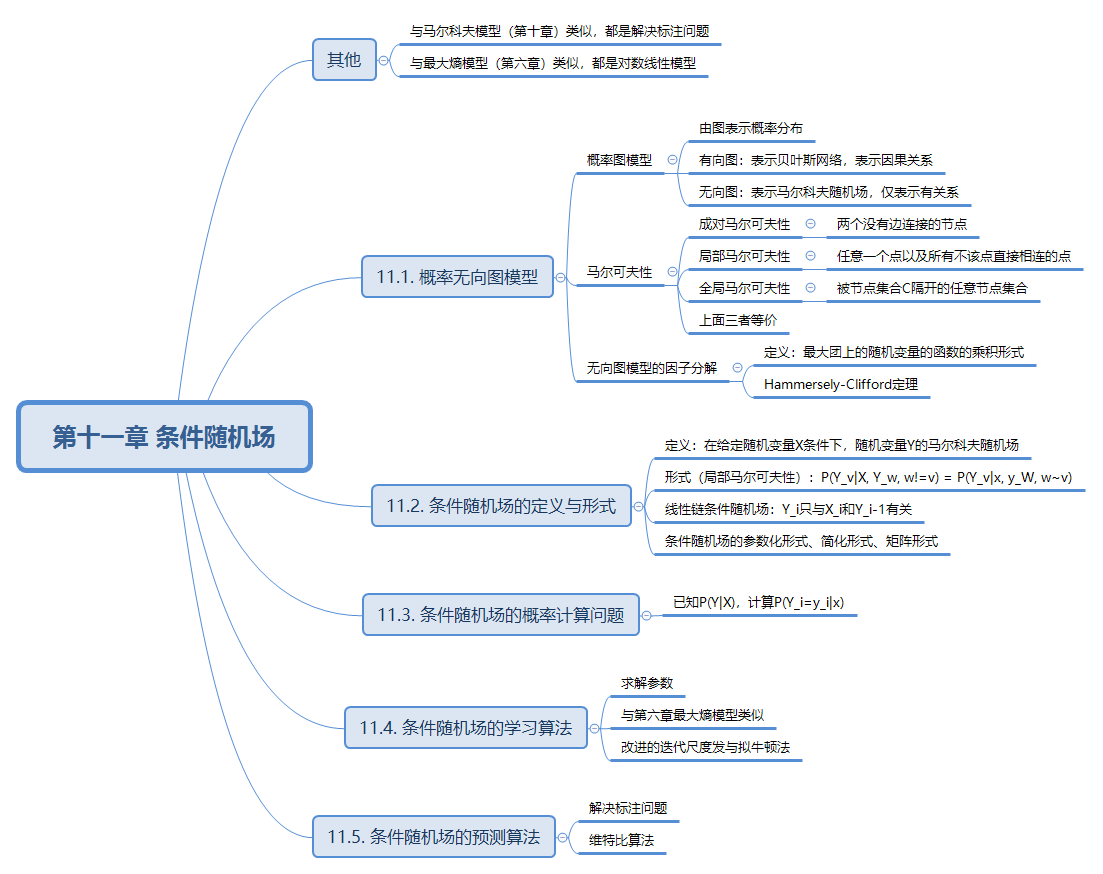
如图上,一共有10个结点(即10个随机变量),任意找两个没有边直接连接的结点,假设有两个随机变量(u,v)没有边相连,剩下的8个随机变量记为O,当给定O时,u和v是独立的,即P(u,v|O)=P(u|O)P(v|O)。
局部马尔可夫性
如上图,任意找一个结点v,与v有边相连的所有结点记为W,其余5个结点记为O,当给定W时,v和O是独立的,即P(v,O|W)=P(v|W)P(O|W)。
全局马尔可夫性
![]()
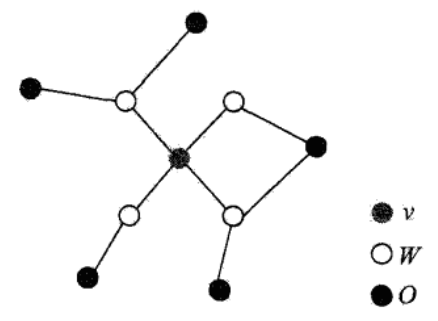
一共有8个结点(即有8个随机变量),取中间两个随机变量记为集合C,当将集合C从图中删掉之后,那么剩下的6个结点分成了两个部分,可知左边的3个结点和右边的3个结点没有任何边将它们相连,当给定C时,A和B是独立的,即P(A,B|C)=P(A|C)P(B|C)。
注意:以上三种马尔可夫性都是等价的。
为什么说这三个马尔可夫性是等价的?这里等价的意思为任意一个结点满足成对马尔可夫性等价于任意一个结点满足局部马尔可夫性,也等价于这些结点满足全局马尔可夫性。
概率无向图模型的因子分解
无向图模型提供了一种分析随机变量之间关系的手段,当已知一组随机变量,能很清楚表达随机变量之间关系的方法是联合概率分布P(Y),根据已知的无向图模型,可以得到联合概率分布P(Y)的形式。
![]()
团:在无向图模型中有一些结点(随机变量),这些结点中任意两个结点都有边相连,这些随机变量组成的集合称为团。如图,Y1和Y2有一条边相连,Y1,Y2可以称为一个团,同理Y2和Y3有一条边相连,Y2,Y3也可以称为一个团,不能将Y1,Y2,Y4称为一个团,因为Y1和Y4之间是没有边相连的,Y1,Y2,Y3可以组成一个团。
最大团:当给定一个团,在该团中不能再加进任何一个结点使其成为更大的团,比如Y1,Y2,Y3就是一个最大团。
\[Hammersley-Clifford定理:\\
概率无向图模型的联合概率分布P(Y)可以表示为如下形式:\\P(Y)=\frac{1}{Z} \prod_C \Psi_C(Y_C) \ Z=\sum_Y \prod_C \Psi_C(Y_C) \\其中,C是无向图的最大团,Y_C是C的结点对应的随机变量,\Psi_C(Y_C)是C上定义的严格正函数,\\乘积是在无向图所有的最大团上进行的,\Psi_C(Y_C) = \exp{-E(Y_C)}。E(Y_C)称为能量函数。
\]
条件随机场(CRF)的的定义与形式
线性链条件随机场
![]()
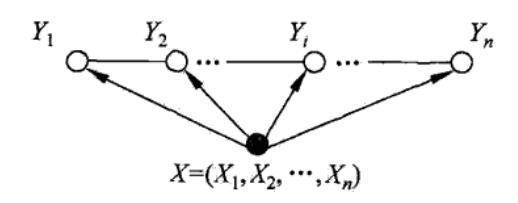
\[如果只考察随机变量Y=(Y_1,Y_2,\cdots,Y_n),这些变量是用无向边连接的,属于无向图(马尔可夫随机场),\\但现在有另一组随机变量X=(X_1,X_2,\cdots,X_n),对每个随机变量Y都产生影响,由于X已知,\\在无向图中就添加了它,X为条件,X和Y合起来称为条件随机场,由于Y是线性连接的,所以称为线性链条件随机场。\\P(Y_v|X,Y_w,w \neq v) = P(Y_v|X,Y_w,w \sim v),其中v表示任意一个结点,w \neq v表示v以外的所有结点\\,w \sim v表示与v有边连接的所有结点,上述等式表示给定X,Y,w的条件下,给定其他所有结点v的分布\\等于给定和它相邻的结点v的分布,其实是局部马尔可夫性。
\]
简化形式
\[P(y|x)=\frac{1}{Z(x)} \exp \sum_{k=1}^K w_k f_k(y,x)\\其中Z(x)=\sum_y \exp \sum_{k=1}^K w_k f_k(y,x) \\ f_k(y_{i-1},y_i,x_i)= \left \{ \begin{array}{l} t_k(y_k,y_i,x,i), \quad k = 1,2,\cdots,K_1 \\ s_l(y_i,x,i), \quad k=K_1+l;l=1,2,\cdots,K_2 \end{array} \right. \\ w_k = \left \{ \begin{array}{l} \lambda_k,\quad k = 1,2,\cdots,K_1 \\ \mu_l, \quad k=K_1+l;l=1,2,\cdots,K_2 \end{array} \right. \\
t_k,s_l是两个特征函数,通常,特征函数t_k,s_l取值为1或0,当满足特征条件时取值为1,否则为0,\\t_k是关于y_i,y_{i-1}特征函数,s_l是关于y_i特征函数,函数t_k称为转移特征,函数s_l称为状态特征。\\条件随机场的参数是\lambda_k,\mu_l。
\]
矩阵形式
\[P_w(y|x)=\frac{1}{Z_w(x)} \prod_{i=1}^{n+1} M_i(y_{i-1}, y_i | x)\\其中Z_w(x)为规范化因子,是n+1个矩阵的乘积的(start,stop)元素:\\Z_w(x)+(M_1(x)M_2(x)\cdots,M_{n+1}(x))_{\text{start},\text{stop}}
\]
推导从参数化形式转化为矩阵形式
\[\because 可以先将对i求和的公共部分给提取出来,如下:\\\begin{array}{ll} {}&\displaystyle \exp \left( \sum_{i,k} \lambda_k t_k(y_{i-1},y_i,x,i) +\sum_{i,l} \mu_l s_l(y_i,x,i) \right) \\ =& \displaystyle \exp\left\{ \sum_i \left[ \sum_k \lambda_k t_k(y_{i-1},y_i,x,i) + \sum_l \mu_l s_l(y_i,x,i) \right] \right\} \\ =& \displaystyle \prod_i \exp\left(\sum_k \lambda_k t_k(y_{i-1},y_i,x,i) + \sum_l \mu_l s_l(y_i,x,i) \right) \end{array}\\
\therefore 可得M_i(y_{i-1},y_i|x) = \exp\left(\sum_k \lambda_k t_k(y_{i-1},y_i,x,i) + \sum_l \mu_l s_l(y_i,x,i) \right)\\ 书中将t_k(y_{i-1},y_i,x,i)和s_l(y_i,x,i)组合成状态函数,将\lambda_k和\mu_l组合成权重向量。\\为什么说M_i(x)是一个矩阵,因为y_{i-1}和y_i都是状态变量,可以通过该公式表示为一个矩阵,得到\\M_i(x)=[M_i(y_{i-1},y_i|x)]
\]
条件随机场的概率计算问题
条件随机场的概率计算问题等价于第10章中求HMM的概率计算问题,利用条件随机场的矩阵形式,计算P(Y=y_i|x),和HMM的区别是求解状态概率,而HMM中是求观测概率,本节采用的算法是前向-后向算法。
前向-后向算法
\[对每个指标i=0,1,2...n+1,定义前向向量\alpha_i(x):\\
\alpha_0(y|x) = \left \{ \begin{array}{l} 1,\quad y=start \\ 0, \quad 否则 \end{array} \right.\\
递推公式:\alpha_i^T(y_i|x)=\alpha_{i-1}^T(y_{i-1}|x)[M_i(y_{i-1},y_i|x)],i=1,2...n+1=\alpha_{i-1}^T(x)M_i(x),\\其中\alpha_i(y_i|x)表示在位置i的标记y_i并且道位置i的前半部分标记序列的非规范化概率,y_i可取的值有m个,\\所以\alpha_i(x)是m维向量。\\同样的,对每个指标i=0,1,2...n+1,定义前向向量\beta_i(x):\\
\beta_{n+1}(y_{n+1}|x) = \left \{ \begin{array}{l} 1,\quad y_{n+1}=stop \\ 0, \quad 否则 \end{array} \right.\\
\beta_i(y_i|x)=[M_i(y_i,y_{n+1}|x)]\beta_{i+1}(y_{i+1}|x)=M_{n+1}(x)\beta_{n+1}(x),\\其中\beta_i(y_i|x)表示位置在i的标记为y_i并且从i+1到n的后半部分标记序列的非规范化概率。\\因此:\\
Z(x)=\alpha_n^T(x) \cdot 1=1^T \cdot \beta_1(x)
\]
条件随机场的学习算法
在对数线性模型中,参数w就是权重,这个权重包含转移特征、状态特征的权重,有两种算法:改进的迭代尺度法,拟牛顿法。这两个算法都用在对数线性模型中。在此处,主要描述拟牛顿法算法。
拟牛顿法
拟牛顿法也是求解最优化问题的一个方法,针对牛顿法的缺陷提出来的新方法。
对此,我们可以先来看下牛顿法——
牛顿法算法描述
\[对于一个无约束的最优化问题\displaystyle \mathop{\min} \limits_{x \in \text{R}^n} f(x)假设f(x)有二阶连续偏导数,使用迭代的方法求解最优解x^*,\\若第k步的迭代值为x^{(k)},将f(x)在x^{(k)}进行二阶泰勒展开:\\f(x)\doteq f(x^{(k)})+\nabla f''(x^{(k)})(x-x^{(k)}) + \frac{1}{2}(x-x^{(k)})^T H(x^{(k)})(x-x^{(k)})\\其中H(x^{(k)})是f(x)的海赛矩阵(Hesse matrix)H(x)=\left[\frac{\partial^2 f}{\partial x_i \partial x_j} \right]_{n \times n}在这点x^{(k)}的值。\\ 函数f(x)有极值,可计算\nabla f(x)=0。\\求极小值:
\nabla f(x) = \nabla f''(x^{(k)})+ H_k(x-x^{(k)}) = 0\\
\therefore x^{(k+1)} = x^{(k)} - H_k^{-1} \nabla f(x^{(k)})
\]
拟牛顿法基本思路
\[1.在迭代的过程中,用一个二次函数逼近每一个迭代的点对应的函数值,如果函数有极小值,需保证该函数是凸函数,\\对应于一维函数中,其二阶导数要大于0,对应于n维的情况,H_k(x^{(k)})是正定矩阵。\\
2.在迭代的过程中需计算H_k^{-1},对于每个k,H_k是不一样的,所以计算H_k^{-1}(n \times n维矩阵)的计算量是非常大的,\\这就是牛顿法的一个缺陷。\\
3.一般在用迭代的方式求解某函数极值时,迭代基本的形式是x^{(k+1)}=x^{(k)}+\lambda p_k,在牛顿法中,更新步长\lambda=1,\\更新方向p_k=- H_k^{-1} \nabla f(x^{(k)}),如果保证是正定的,就可以保证这是一个向下的方向(可以达到收敛)\\
4.除了牛顿法,在梯度下降法中,迭代形式是x^{(k+1)}=x^{(k)}-\lambda \nabla f(x^{(k)}),在\lambda比较小时,\\可以保证使得f(x)下降的方向,只用到了f(x)在点x^{(k)}的一阶导,对应到多维中就是梯度。\\而在牛顿法中,用到了一阶导和二阶导,因为牛顿法用了二阶导,比梯度下降法更快,\\即能更快地找到f(x)取极小值对应的x^*。
\]
1.在这里为何提到要保证函数必须是凸函数呢?假如一个函数不是凸函数,那么可以想象函数图像类似一堆沙滩凹凸不平,那么如果寻优的结果可能得到多个极小值,只是局部最优,而不是全局最优,此时寻找最优解难度比较大。
2.为何要求海塞矩阵满足正定?
首先需要清楚明白什么是正定矩阵。
\[A是n阶方阵,如果对任何非零向量x,都有x^TAx>0,其中x^T 表示x的转置,就称A正定矩阵。
\]
由此可以看出,在迭代过程中,更新的方向就是向下的。并且满足正定时,f(x)能取得唯一的极小值。
预测算法
和HMM一样,采用维特比算法(动态规划求解最优路径)。具体运用和计算方式可以看书中的例子。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号