java期中考试及4、5次作业简评
一、 前言
无论是期中考试还是4、5次大作业,题目每题之间都是密不可分的,比如第一题写好的代码你在第二题中可能就要用它作为一个子类。期中考试没有取得好成绩,一方面是因为第一次正式考试,没有实战经验,导致到了考试时间还没有将代码提交上去的情况,少拿了很多分。但是归根到底,这还是我知识不够扎实的原因,如果基础知识足够扎实,无论是什么题目都不应该出现时间不够的问题。而第4、5次作业是在前几次作业上的再次拓展,由三角形拓展到四边形,再由四边形拓展到五边形,这无疑极大的增加了题目的复杂度,不仅因为之前基础子类体系没有完善好,再加上五边形的各情况要求判断十分复杂,这都让题目变得十分棘手。但总的来说,题目是老师精心挑选出来的,题量以及难易度肯定是没得说,都在可接受范围内,只要我们认真结合老师点拨与网络资源,这几次作业可以成为我们学习路上典例中的典例,值得不断探索学习。
二、 设计与分析
(1) 期中考试第一题比较简单,题目明确了点类与线类中应该有的属性与方法,只要按题目要求一步步将类设计好即可。
例如

按题目要求写出相应属性方法即可
此类题型在于考察对类的基础知识掌握,类中的数据都应设计为私有,再通过set()、get()函数对属性进行更改。极大的增强了数据的安全性。是我们必须要掌握的基础知识。
(2) 期中考试第二题在第一题基础上设计父类实现继承与多态。同样,题目要求清楚明确,按要求往下走即可。
例如

创建一个element父类,定义display方法,为后续多态输出做准备。

如在线类中定义自己的display方法并继承element类。

在输出时调用父类的display方法,此时子类中diaplay方法将覆盖父类中方法,实现多态输出。
(3) 期中考试第三题为在第二题基础上增加容器类来存放每一个点线面对象,再对容器进行增加、删除、遍历等操作。

设计容器类,并添加增加、删除、查询等操作。

在main函数中对输入的选择进行不同的操作以达到题目要求。
1 while(choice != 0) { 2 switch(choice) { 3 case 1://insert Point object into list 4 double x1 = in.nextDouble(); 5 double y1 = in.nextDouble(); 6 if(!(x1>0&&x1<=200&&y1>0&&y1<=200)) { 7 System.out.println("Wrong Format"); 8 return; 9 } 10 Point p1 = new Point(x1,y1); 11 g.add(p1); 12 break; 13 case 2://insert Line object into list 14 double x2 = in.nextDouble(); 15 double y2 = in.nextDouble(); 16 double x3 = in.nextDouble(); 17 double y3 = in.nextDouble(); 18 if(!(x2>0&&x2<=200&&x3>0&&x3<=200&&y2>0&&y2<=200&&y3>0&&y3<=200)) { 19 System.out.println("Wrong Format"); 20 return; 21 } 22 Point p2 = new Point(x2,y2); 23 Point p3 = new Point(x3,y3); 24 String color = in.next(); 25 Line line = new Line(p2,p3,color); 26 g.add(line); 27 break; 28 case 3://insert Plane object into list 29 String color1 = in.next(); 30 Plane plane = new Plane(color1); 31 g.add(plane); 32 break; 33 case 4://delete index - 1 object from list 34 int index = in.nextInt(); 35 if(!(index<1||index>g.getelements().size())) 36 g.remove(index-1); 37 } 38 39 } 40 for(int i=0;i<=g.getelements().size();i++) { 41 g.getelements().get(i).display(); 42 }
其中最难也是最易出错的部分在于对容器内第index个对象进行删除操作时的数据合法性判断,一旦混淆便会出现越界报错,我当时考试便是因为越界而耽误了许多时间导致代码未提交。不过这也正能让我在以后的编程过程中时刻注意此类问题,避免再犯。
(4)第4次作业主要为对四边形的一系列判断,基于三角形的操作,拓展到四边形。而另外俩个分别为对正则表达式的运用以及对类的基础知识的运用,只要认真阅读理解题目意思,按题目要求一步步走即可满分,在此便不在深入讨论。
在四边形相关计算中,容易出错的点在于对凹凸四边形的判断以及排除冗余点以及计算直线分割之后的面积。
对于凹凸四边形,我的算法是四边形四个点分别构成四个三角形,判断相对的俩个三角形面积相加是否等于另外两个三角形面积相加,若相等则为凸四边形,不相等则为凹四边形。
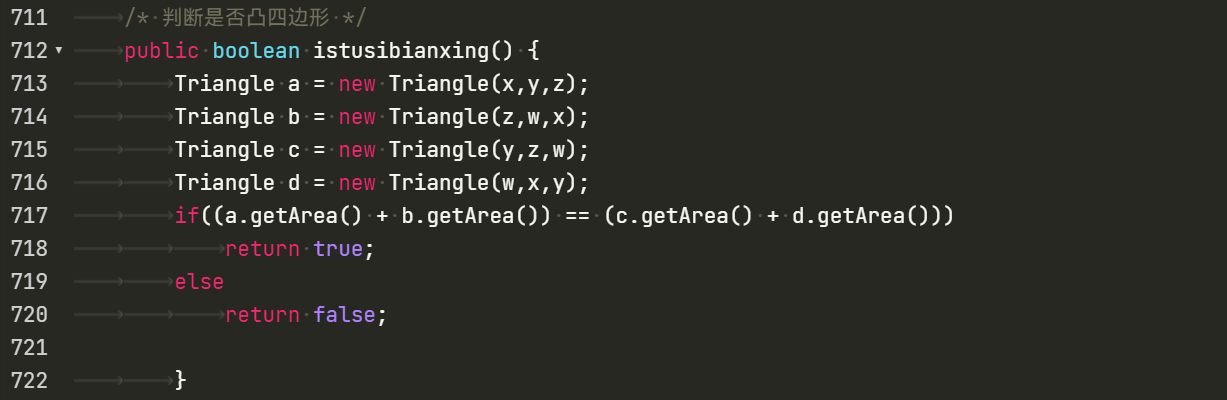
对于冗余点的排除,此算法我在下一次五边形作业中才研究出来,此题暂未排除冗余点,只适用于少部分情况。
分割面积算法我也没有研究出来,只写出了判断交点个数的算法。
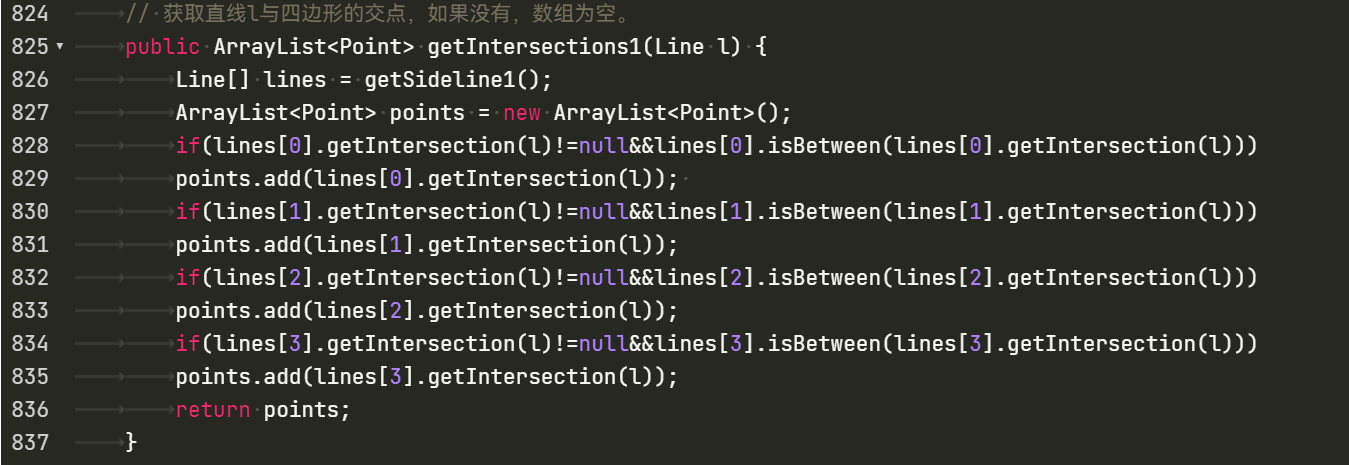
通过判断返回的points容器大小来判断点的个数。
(5)第五次作业是在第四次作业四边形的基础上拓展为五边形,有许多算法与四边形类似但又有些不一样。
如果用户选择计算1,输入五个点坐标,判断是否是五边形,判断结果输出true/false。算法原理为判断五边形每条边与邻边不平行且与隔边无交点。
1 public boolean is五边形() { 2 Line l1 = new Line(x, y); 3 Line l2 = new Line(y, z); 4 Line l3 = new Line(z, w); 5 Line l4 = new Line(w, v); 6 Line l5 = new Line(v, x); 7 if(l1.isParallel(l2)|| l1.isParallel(l5)|| l3.isParallel(l2)|| l3.isParallel(l4)||l4.isParallel(l5)) 8 return false; 9 else if(l1.getIntersection(l3)!=null) { 10 if(l1.isBetween(l1.getIntersection(l3))&& l3.isBetween(l1.getIntersection(l3))) { 11 return false; 12 } 13 else { 14 return true; 15 } 16 } 17 else if(l2.getIntersection(l4)!=null) { 18 if(l2.isBetween(l2.getIntersection(l4))&& l4.isBetween(l2.getIntersection(l4))) { 19 return false; 20 } 21 else { 22 return true; 23 } 24 } 25 else if(l3.getIntersection(l5)!=null) { 26 if(l3.isBetween(l3.getIntersection(l5))&& l5.isBetween(l3.getIntersection(l5))) { 27 return false; 28 } 29 else { 30 return true; 31 } 32 } 33 else 34 return true; 35 }
如果用户选择计算2,输入五个点坐标,判断是凹五边形(false)还是凸五边形(true),如果是凸五边形,则再输出五边形周长、面积,结果之间以一个英文空格符分隔。 若五个点坐标无法构成五边形,输出"not a pentagon"。
算法原理为利用向量叉乘判断是否为凸五边形。
1 public boolean is凸五边形() { 2 Line[] ls = getSideline(); 3 double v0 = ls[0].getchaji(ls[1]); 4 double v1 = ls[1].getchaji(ls[2]); 5 double v2 = ls[2].getchaji(ls[3]); 6 double v3 = ls[3].getchaji(ls[4]); 7 double v4 = ls[4].getchaji(ls[0]); 8 if(v0 * v1 < 0 || v0 * v2 < 0 || v0 * v3 < 0 || v0 * v4 <0) { 9 return false; 10 } 11 else 12 return true; 13 } 14 public double getchaji(Line line) { 15 Point p1 = new Point(); 16 Point p2 = new Point(); 17 p1 = this.getPointA(); 18 p2 = this.getPointB(); 19 double s =(p1.getX()*p2.getY()-p1.getY()*p2.getX()); 20 return s; 21 }
如果用户选择计算3,输入七个点坐标,前两个点构成一条直线,后五个点构成一个凸五边形、凸四边形或凸三角形,输出直线与五边形、四边形或三角形相交的交点数量。如果交点有两个,再按面积从小到大输出被直线分割成两部分的面积(不换行)。若直线与多边形形的一条边线重合,输出"The line is coincide with one of the lines"。若后五个点不符合五边形输入,若前两点重合,输出"points coincide"。
首先逐层判断五个点构成的多边形,再判断线重合或点重合的情况,最后判断面积大小。
1 public static void handle3(ArrayList<Point> ps) { 2 PointInputError.wrongNumberOfPoints(ps, 7); 3 Line l = new Line(ps.get(0), ps.get(1)); 4 五边形 t = new 五边形(ps.get(2), ps.get(3), ps.get(4),ps.get(5),ps.get(6)); 5 if(ps.get(0).equals(ps.get(1))) { 6 System.out.println("points coincide"); 7 return; 8 } 9 10 if(t.is五边形()) { 11 if(t.judgeLineCoincide(l)) { 12 System.out.println("The lineis coincide with one of the lines"); 13 return; 14 } 15 ArrayList<Point> p0 = t.getIntersections(l); 16 System.out.println(p0.size()); 17 } 18 else 19 { 20 ArrayList<Point> p = new ArrayList<Point>(); 21 p=t.judgefivepoints(ps.get(2), ps.get(3), ps.get(4), ps.get(5), ps.get(6)); 22 Triangle t1 = new Triangle(p.get(0), p.get(1), p.get(2),p.get(3)); 23 if(t1.isTriangle()) { 24 if(t1.judgeLineCoincide1(l)) { 25 System.out.println("The lineis coincide with one of the lines"); 26 return; 27 } 28 ArrayList<Point> p0 = t1.getIntersections(l); 29 System.out.println(p0.size()); 30 } 31 else { 32 ArrayList<Point> p1 = new ArrayList<Point>(); 33 p1=t1.judgefourpoints(p.get(0), p.get(1), p.get(2), p.get(3)); 34 Triangle t2 = new Triangle(p1.get(0), p1.get(1), p1.get(2)); 35 if(t2.istriangle()) { 36 if(t2.judgeLineCoincide(l)) { 37 System.out.println("The lineis coincide with one of the lines"); 38 return; 39 } 40 ArrayList<Point> p0 = t2.getIntersections(l); 41 System.out.println(p0.size()); 42 } 43 else 44 System.out.println("not a polygon"); 45 } 46 } 47 }
如果用户输入计算4,输入十个点坐标,前、后五个点分别构成一个凸多边形(三角形、四边形、五边形),判断它们两个之间是否存在包含关系(一个多边形有一条或多条边与另一个多边形重合,其他部分都包含在另一个多边形内部,也算包含)。两者存在六种关系:1、分离(完全无重合点) 2、连接(只有一个点或一条边重合) 3、完全重合 4、被包含(前一个多边形在后一个多边形的内部)5、交错 6、包含(后一个多边形在前一个多边形的内部)
首先通过函数判断前后俩个多边形的形状,再根据不同情况分别讨论输出。
1、分离的判定方法为俩多边形的各点均在对方外部。
1 public boolean judge分离(五边形 t,int i){ 2 if(i==1) { 3 ArrayList<Point> p1 = new ArrayList<Point>(); 4 p1 = t.returnpoints(); 5 if(this.isInside(p1.get(0))==-1&&this.isInside(p1.get(1))==-1&&this.isInside(p1.get(2))==-1&&this.isInside(p1.get(3))==-1&&this.isInside(p1.get(4))==-1) 6 return true; 7 } 8 else 9 if(i==2) { 10 ArrayList<Point> p1 = new ArrayList<Point>(); 11 p1 = t.returnpoints(); 12 if(this.isInside(p1.get(0))==-1&&this.isInside(p1.get(1))==-1&&this.isInside(p1.get(2))==-1&&this.isInside(p1.get(3))==-1) 13 return true; 14 } 15 else 16 if(i==3) { 17 ArrayList<Point> p1 = new ArrayList<Point>(); 18 p1 = t.returnpoints(); 19 if(this.isInside(p1.get(0))==-1&&this.isInside(p1.get(1))==-1&&this.isInside(p1.get(2))==-1) 20 return true; 21 } 22 return false; 23 }
2、连接的判定方法为只有一个点或一条边重合。
1 public boolean judge连接(五边形 t,int i){ 2 if(i==1) { 3 4 if(this.isInside(t.x)==0&&this.isInside(t.y)!=0&&this.isInside(t.w)!=0&&this.isInside(t.z)!=0&&this.isInside(t.v)!=0 5 ||this.isInside(t.x)!=0&&this.isInside(t.y)==0&&this.isInside(t.w)!=0&&this.isInside(t.z)!=0&&this.isInside(t.v)!=0 6 ||this.isInside(t.x)!=0&&this.isInside(t.y)!=0&&this.isInside(t.w)==0&&this.isInside(t.z)!=0&&this.isInside(t.v)!=0 7 ||this.isInside(t.x)!=0&&this.isInside(t.y)!=0&&this.isInside(t.w)!=0&&this.isInside(t.z)==0&&this.isInside(t.v)!=0 8 ||this.isInside(t.x)!=0&&this.isInside(t.y)!=0&&this.isInside(t.w)!=0&&this.isInside(t.z)!=0&&this.isInside(t.v)==0 9 ||this.judge边重合(t, 1)) 10 return true; 11 } 12 else 13 if(i==2) { 14 ArrayList<Point> p1 = new ArrayList<Point>(); 15 p1 = t.returnpoints(); 16 if(this.isInside(p1.get(0))==0&&this.isInside(p1.get(1))!=0&&this.isInside(p1.get(2))!=0&&this.isInside(p1.get(3))!=0 17 ||this.isInside(p1.get(0))!=0&&this.isInside(p1.get(1))==0&&this.isInside(p1.get(2))!=0&&this.isInside(p1.get(3))!=0 18 ||this.isInside(p1.get(0))!=0&&this.isInside(p1.get(1))!=0&&this.isInside(p1.get(2))==0&&this.isInside(p1.get(3))!=0 19 ||this.isInside(p1.get(0))!=0&&this.isInside(p1.get(1))!=0&&this.isInside(p1.get(2))!=0&&this.isInside(p1.get(3))==0 20 ||this.judge边重合(t, 2)) 21 return true; 22 } 23 else 24 if(i==3) { 25 ArrayList<Point> p1 = new ArrayList<Point>(); 26 p1 = t.returnpoints(); 27 if(this.isInside(p1.get(0))==0&&this.isInside(p1.get(1))!=0&&this.isInside(p1.get(2))!=0 28 ||this.isInside(p1.get(0))!=0&&this.isInside(p1.get(1))==0&&this.isInside(p1.get(2))!=0 29 ||this.isInside(p1.get(0))!=0&&this.isInside(p1.get(1))!=0&&this.isInside(p1.get(2))==0 30 ||this.judge边重合(t, 3)) 31 return true; 32 } 33 return false; 34 }
3、完全重合的判定方法为俩多边形的各点均在对方边上。
1 public boolean judge重合(五边形 t){ 2 if(this.isInside(t.x)==0&&this.isInside(t.y)==0&&this.isInside(t.z)==0&&this.isInside(t.w)==0&&this.isInside(t.v)==0) { 3 return true; 4 } 5 return false; 6 }
4、包含与被包含判定为多边形的各点均在对方内部。
1 public boolean judge包含(五边形 t,int i){ 2 if(i==1) { 3 ArrayList<Point> p1 = new ArrayList<Point>(); 4 p1 = t.returnpoints(); 5 if(this.isInside(p1.get(0))==1&&this.isInside(p1.get(1))==1&&this.isInside(p1.get(2))==1&&this.isInside(p1.get(3))==1&&this.isInside(p1.get(4))==1) 6 return true; 7 } 8 else 9 if(i==2) { 10 ArrayList<Point> p1 = new ArrayList<Point>(); 11 p1 = t.returnpoints(); 12 if(this.isInside(p1.get(0))==1&&this.isInside(p1.get(1))==1&&this.isInside(p1.get(2))==1&&this.isInside(p1.get(3))==1) 13 return true; 14 } 15 else 16 if(i==3) { 17 ArrayList<Point> p1 = new ArrayList<Point>(); 18 p1 = t.returnpoints(); 19 if(this.isInside(p1.get(0))==1&&this.isInside(p1.get(1))==1&&this.isInside(p1.get(2))==1) 20 return true; 21 } 22 return false; 23 }
5、交错判定方法为除去上述五种情况后剩余俩多边形的位置关系即交错。

如果用户选择计算5,输入十个点坐标,前、后五个点分别构成一个凸多边形(三角形、四边形、五边形),输出两个多边形公共区域的面积。
此题我只判断了多边形构成,未计算面积。
如果用户选择计算6,输入六个点坐标,输出第一个是否在后五个点所构成的多边形(限定为凸多边形,不考虑凹多边形),的内部(若是五边形输出in the pentagon/outof the pentagon,若是四边形输出in the quadrilateral/outof the quadrilateral,若是三角形输出in the triangle/outof the triangle)。
同样先判断多边形形状,再运用之前的各个判断点是否在内部的方法进行输出。
1 PointInputError.wrongNumberOfPoints(ps, 6); 2 五边形 t = new 五边形(ps.get(1), ps.get(2), ps.get(3),ps.get(4),ps.get(5)); 3 if(t.is五边形()) { 4 if(t.isInside(ps.get(0))==0) { 5 System.out.println("on the pentagon"); 6 return; 7 } 8 else 9 if(t.isInside(ps.get(0))==1) { 10 System.out.println("in the pentagon"); 11 return; 12 } 13 else 14 if(t.isInside(ps.get(0))==-1) { 15 System.out.println("outof the pentagon"); 16 return; 17 } 18 } 19 else 20 { 21 ArrayList<Point> p = new ArrayList<Point>(); 22 p=t.judgefivepoints(ps.get(1), ps.get(2), ps.get(3), ps.get(4), ps.get(5)); 23 Triangle t1 = new Triangle(p.get(0), p.get(1), p.get(2),p.get(3)); 24 if(t1.isTriangle()) { 25 if(t1.isInside1(ps.get(0))==0) { 26 System.out.println("on the quadrilateral"); 27 return; 28 } 29 else 30 if(t1.isInside1(ps.get(0))==1) { 31 System.out.println("in the quadrilateral"); 32 return; 33 } 34 else 35 if(t1.isInside1(ps.get(0))==-1) { 36 System.out.println("outof the quadrilateral"); 37 return; 38 } 39 } 40 else { 41 ArrayList<Point> p1 = new ArrayList<Point>(); 42 p1=t1.judgefourpoints(p.get(0), p.get(1), p.get(2), p.get(3)); 43 Triangle t2 = new Triangle(p1.get(0), p1.get(1), p1.get(2)); 44 if(t2.istriangle()) { 45 if(t2.isInside(ps.get(0))==0) { 46 System.out.println("on the triangle"); 47 return; 48 } 49 else 50 if(t2.isInside(ps.get(0))==1) { 51 System.out.println("in the triangle"); 52 return; 53 } 54 else 55 if(t2.isInside(ps.get(0))==-1) { 56 System.out.println("outof the triangle"); 57 return; 58 } 59 } 60 else 61 System.out.println("not a polygon"); 62 } 63 } 64 }
三、踩坑心得
对于这几次作业,遇到了非常多问题,大多是因为自身基础知识不扎实而导致的。常见的有因为一开始没有意识到对冗余点进行排除的算法的重要性,导致先前代码有许多可替换部分,使用判断形状函数不仅可以使代码简洁合理,更能完善算法,考虑情况更加全面。另外代码重复性高也是这几次作业的通病,没有好好思考如何合理排布代码,灵活运用方法将代码简洁化。
使用returnpoints函数返回排除掉冗余点的剩余点,可大大简化代码,每次判断形状可使用此函数。
1 public ArrayList<Point> returnpoints() { 2 ArrayList<Point> ps = new ArrayList<Point>(); 3 if(this.is五边形()) { 4 return this.getpoints(); 5 } 6 else 7 { 8 ArrayList<Point> p = new ArrayList<Point>(); 9 p=this.judgefivepoints(this.x, this.y, this.z, this.w,this.v); 10 Triangle t1 = new Triangle(p.get(0), p.get(1), p.get(2),p.get(3)); 11 if(t1.isTriangle()) { 12 return t1.getpoints1(); 13 } 14 else { 15 ArrayList<Point> p1 = new ArrayList<Point>(); 16 p1=t1.judgefourpoints(p.get(0), p.get(1), p.get(2), p.get(3)); 17 Triangle t2 = new Triangle(p1.get(0), p1.get(1), p1.get(2)); 18 if(t2.istriangle()) { 19 return t2.getpoints(); 20 } 21 else 22 return ps; 23 } 24 } 25 }
(4)改进建议
应在程序中更加凸显类与对象这一概念,有许多可由之前写过的代码衍生而来的算法都未很好的利用起来,没有明确的类的定义,导致后面要用之前的算法时只能复制黏贴这样的笨办法,应多学习如何通过类之间的关系做到灵活调用方法,为代码的可移植性打好基础。实际上题目的层次关系十分明显,就是为了引导我们能够实现方法的调用,以后做题学习时应多注意此类关系紧密的类型,尽力完善方法间的套用关系。完善类的同时,算法的优化也十分重要,算法优化不仅可以节省时间提高效率,还可以使程序更加简洁美观。
(5)总结
通过这三次作业的学习,我初步认识到了java面向对象的编码理念,掌握了一些基本的类的操作,通过对象来管理属性,对数据格式的基础判断,java一些快捷语句的使用等等。同时也发现了自身许多问题,类的具象化还是不够完整清楚,不能让人直观明了,导致代码繁琐,复杂度高,阅读起来很困难,这都是需要改进的地方。老师课程与慕课等平台课程结合学习可以使学习效率最大化,老师也可以在课堂上与慕课内容互动联系,使学生更加印象深刻。作业的质量很高,难度适中且具一定挑战性,希望老师能继续出类似的高质量题目,为我们学习成长夯实基础,铸就典例。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号