用组合提高软件测试用例的生成
英文原文:http://msdn.microsoft.com/zh-cn/magazine/cc163957(en-us).aspx
原文作者:Dr. James McCaffrey
测试一直是软件开发过程中的一个重要过程,而三个因素使得它扮演了更重要的角色。首先,微软.Net的环境已经显著地提高了程序员编写自定义自动化测试的能力,以前需要两周时间创建的测试项目,现在在.Net Framework下只用几个小时便可完成。第二,程序和系统越趋于复杂,所需的测试就越精密。最后,软件安全性已不再是程序开发最后才考虑的问题,它是绝对必要的。在以前有可能存在一款软件没有经过完整的测试就已向外发布的情况,但如今这已不再可行。为了帮助你满足现今的测试挑战,我将在这个栏目里每隔几个月就向你展示软件测试的最佳方法、原则和技术。
这个月我将从组合在软件测试中的角色开始说起。编程产生组合的能力,能够为你的测试用例输出提供强有力的方法。首先我谈谈我所说的组合的意思:如果你现在正在写一个扑克牌的程序,需要你手动输入5张牌牌型的所有可能情况,你一定不会乐意。但如果你用这个栏目里的代码来处理,你将能够在几分钟内做好这件事:
Combination c = new Combination(52,5); // 52 cards, 5 at a time
string[] pokerHand = new string[5];
while (c != null)
{
pokerHand = c.ApplyTo(deck);
PrintHand(pokerHand);
c = c.Successor();
}
在大量的自动化测试方案中,你一旦学习并认识了组合,你会发现它惊人的有用。再举一个例子,假如你正在测试某个系统,要用户从文本框接收用户传入的10个字符。用户可能会输入"ABCDEFGHIJ",或者是")(*&^%$#@!",你想知道共有多少种测试的用例。假定你要求输入字符的可选类型等于20种(这可能根据系统要求的不同而不同,比如从大写的'A'到'Z',或者是从0到9等等)。
要特别强调的是,你必须从20个不同的字符中一次性选取10个,即Choose(20,10)——这个函数我会在稍后解释。请注意,这里我其实简化了问题。实际上,你可能还需要考虑每个边界条件和其他测试概念的排列组合。
现在,我将会创建一个C#语言写的的组合类,并向你展示怎样用组合来提高测试的性能。我想你一定会认为理解并运用组合及其相关的理论是有价值的。
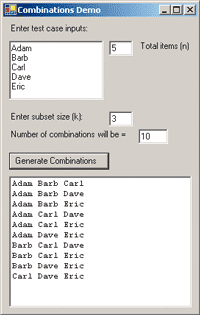
图1 Combinations Demo
贴上截图是让你能够跟上我思路的最好方式。图1是一个Windows@-based 应用程序的截图,它演示了组合的应用。正如你所看见的,组合就是一组元素的无序子集。在这个例子中我们有5个元素——Adam,Barb,Carl,Dave和Eric——我只对3个元素的组合感兴趣。从5个元素中一次性选出3个,共有10种不同组合:
注意,无序子集的意思是,{Carl,Barb,Adam}和{Adam,Barb,Carl}是等价的,两者都代表同一个子集。图1还说明了一点,在用给定的元素集合大小和子集大小生成组合时,我们还需要计算出不同组合的总数。
数学中组合的定义是:n是从整数0到n-1的集合,从4个元素的集合中一次选取2个的6种组合即是:
{ 0, 2 } { 1, 3 }
{ 0, 3 } { 2, 3 }
正如我之前所说,组合在软件测试、开发、管理等各种领域中都有着很大的作用。组合在数学领域中是古典而又深刻的,但我发现有很多程序员对它的理解都不够彻底,现有网络中的一些与组合相关的代码不是写错了,就是执行效率低下。
组 合
在图2中描述了数学组合中的三个必要操作,输出的结果会告诉你,当n=4,k=2时共有6中组合:
{ 0, 2 } { 1, 3 }
{ 0, 3 } { 2, 3 }
从这个例子可以看出,给定了集合中元素的数量,以及子集的大小,我们就能够计算出一共有多少种组合,并列举出所有的组合情况。
图2 组合
{
long n = 4;
long k = 2;
Console.WriteLine("With n = " + n + ", and k = " + k);
Console.WriteLine("There are " + Combination.Choose(n,k) +
"combinations\n");
Combination c = new Combination(n,k);
Console.WriteLine("The mathematical combinations are:");
while (c != null)
{
Console.WriteLine(c.ToString());
c = c.Successor();
}
Console.ReadLine();
}
仔细观察,你会发现组合有两个重要的参数:集合中元素的数量(数学中常常用n来表示)和子集的大小(常常用k表示)。组合在数学领域中有0型组合和1型组合。接下来的例子我所指的都是0型组合,并用我们所熟知的n、k来表示。
在我之前例子中的组合都是用字典序枚举的。在数学的整型数中,这种排序即为递增的排序。例如当n=5,k=3时,组合的第一个元素是{0,1,2},下一个元素是{0,1,3},因为12在13之前。
组合中的一个重要函数是根据n和k计算出不同组合的总个数。这个函数常叫做Choose。因此在最开始5个人名的例子中,我们可以表示为Choose(5,3)=10,这表示从5个元素中一次选3个,共有10种不同的组合。 你可能会看见有许多其他的函数名表示同样的意思,但这边文章里我都用Choose来表示。
Choose函数中的n和k很容易被人混淆。一种数学中的组合n=7,k=4(7个元素一次选4个)的其中一种组合便是{0,3,4,6},而Choose(7,4)返回值则是35。
人们常常把组合与排列混淆,排列是一个有序的集合,在排列中{Alex,Bill,Cris,Doug},{Alex,Bill,Doug,Cris}和{Alex,Cris,Bill,Doug}是不同的集合。
组合类
数学中的组合能够很漂亮的被描述为类。首选你需要定义n和k,以及一个元素的数组。在图3中我们定义了组合的一些基本元素,其中构造函数用递增的长整型整数初始化了data元素数组。我建议你使用C#语言,但你也可以用.Net平台的其他语言,转换是很容易的。
图3 组合类的定义
{
private long n = 0;
private long k = 0;
private long[] data = null;
public Combination(long n, long k)
{
if (n < 0 || k < 0) // normally n >= k
throw new Exception("Negative parameter in constructor");
this.n = n;
this.k = k;
this.data = new long[k];
for (long i = 0; i < k; ++i)
this.data[i] = i;
}
public override string ToString()
{
StringBuilder sb = new StringBuilder();
sb.Append("{ ");
for (long i = 0; i < this.k; ++i)
sb.AppendFormat("{0} ", this.data[i]);
sb.Append("}");
return sb.ToString;
}
我把这段代码放在一个控制台应用程序中编译之后,执行了如下命令:
Console.WriteLine("\nCombination c(5,3) is initially " + c.ToString());
程序的输出结果是:
当程序执行第一条语句时:
这表示从5个元素一次选取3个的组合,这时在内存中已经生成了按字典排序的组合中的第一个元素。见图4。

图4 内存中的对象
构造函数快速地创建了组合中的第一个元素。因为我们要处理的数据的值可能很大,所以我选择用C#的长整型long代替短整型int,如果还想扩大数值范围,我们可以用无符号长整型ulong。我用从0到k-1的k个整数填充data的数组。
计算组合的总数
接下来我们将讨论,如何计算组合的总数。例如当n=5,k=3时共有10种组合:
{ 0, 1, 3 } { 1, 2, 3 }
{ 0, 1, 4 } { 1, 2, 4 }
{ 0, 2, 3 } { 1, 3, 4 }
{ 0, 2, 4 } { 2, 3, 4 }
标准的Choose(n,k)函数直接用的是组合公式的定义,虽然标准,但是解决问题的能力很有限,代码如下:
static int Choose(int n, int k)
{
int numerator = Factorial(n);
int denominator = Factorial(k) * Factorial(n-k);
return ( numerator / denominator );
}
其中Factorial是计算阶乘:
{
int ans = 1;
for (int i = m; i >= 1; —-i)
{
ans = ans * i;
}
return ans;
}
这个Choose函数有个很严重的问题,即使是不大的n和k都有可能造成堆栈溢出。仔细观察这个Choose函数,它先计算了n的阶乘,这就很容易得到一个巨大的值,即使n很小(例如,n=21,试试计算21!),用64位无符号整型的变量存储很快便会溢出。Choose(n,k)要计算的其实是两个数的商,这两个数都可能很大,但是他们的商却相对小很多。这个方法的问题就是:即使最后我们计算出的结果很小,但是在计算的过程中却会产生很大的数而导致溢出。
一个较好的方法计算Choose(n,k)可以用下面的等价公式:
下面的代码是一个例子:
这样就避免了直接计算n的阶乘,在运算中,你也可以先做一部分除法以减小运算量,例如Choose(7,3),你可以先计算7*6,再除以2,得到24,然后*5在除以3,得到最终结果35。
第二个优化是利用下面的等价公式:
例如Choose(10,8)=Choose(10,2)。这个关系可能不容易想象,但是你可以自己举几个简单的例子计算,结果确实如此。计算Choose(10,8)需要计算7次乘法以及7次除法,而Choose(10,2)则只需1次乘法和1次除法。
把这些想法结合起来,我们便可以优化以前的Choose(n,k)方法,如图5。在Choose函数中,我判断了如果n等于k则直接返回1。这在之前的理论并没有提到,但是这可以有效提高程序的性能。
图5 优化的Choose方法
{
if (n < 0 || k < 0)
throw new Exception("Invalid negative parameter in Choose()");
if (n < k) return 0;
if (n == k) return 1;
long delta, iMax;
if (k < n-k) // ex: Choose(100,3)
{
delta = n-k;
iMax = k;
}
else // ex: Choose(100,97)
{
delta = k;
iMax = n-k;
}
long ans = delta + 1;
for (long i = 2; i <= iMax; ++i)
{
checked { ans = (ans * (delta + i)) / i; }
}
return ans;
}
生成所有的组合元素
第三个优化是处理生成组合元素的函数。网络上的这类函数都缺乏效率,我们下面就简单地看看一个典型的生成组合的方法,然后我再优化它。
假如你有4个元素——Adam,Barb,Carl,Dave——从中一次选取2个,输出所有的组合元素。代码如下:
Console.WriteLine("\nAll elements of 4 names, 2 at a time: ");
string[] names = {"Adam", "Barb", "Carl", "Dave"};
for (int i = 0; i < names.Length; ++i)
{
for (int j = i+1; j < names.Length; ++j)
{
Console.WriteLine( "{ " + names[i] + ", " + names[j] + " }" );
}
}
运行代码,“正确”的结果如下:
{ Barb, Dave }, { Carl, Dave }.
但是这里有三个问题。首先,这个方法能够如你所愿的生成所有组合,但如果你只是想要一部分组合而并非所有呢?第二,此方法只是用于特殊问题,并不具有通用性。第三,当k值很小时,它能够做得很好,但是如果k很大呢?如果是要从100个元素中选取50个,你将不得不做50次代码循环或者是递归。
Successor函数是一个生成组合的更好的解决方案,它它只根据给定的组合元素生成下一个组合元素。如果你结合Successor函数和ApplyTo函数来生成组合,将会变得非常高效。
图6是Successor的代码,它首先检查是否还有下一个组合元素。例如,当n=5,k=3是,10个组合元素如下:
{ 0, 1, 3 } { 1, 2, 3 }
{ 0, 1, 4 } { 1, 2, 4 }
{ 0, 2, 3 } { 1, 3, 4 }
{ 0, 2, 4 } { 2, 3, 4 }
图6 元素的字典下一个组合
{
if (this.data.Length == 0 ||
this.data[0] == this.n - this.k)
return null;
Combination ans = new Combination(this.n, this.k);
long i;
for (i = 0; i < this.k; ++i)
ans.data[i] = this.data[i];
for (i = this.k - 1; i > 0 && ans.data[i] == this.n - this.k + i; --i);
++ans.data[i];
for (long j = i; j < this.k - 1; ++j)
ans.data[j+1] = ans.data[j] + 1;
return ans;
}
请注意,我们都知道组合字典的最后一个元素是{2,3,4},因为只有这个元素的开头是数字2,2刚好是等于n-k的,也就是说,在位置0有值n-k。这个结果是对所有组合都成立的。同样,你可以知道组合字典的第一个元素是{0,1,2},因为只有这个元素的末尾是数字2,也就是说,在k-1的位置有值k-1,同样这个结果是具有普遍性的。Successor函数会在找不到下一个组合元素时返回空值。
这个Successor函数并没有用什么特别的技巧,我们只是从元素的最右边位置开始做递增地改变,直到最后改变到最左边的元素。每一次改变,我们都从位置i开始递增,然后重置i右边的所有元素,重置的方法是该位置的值比它左边一个位置的值大1。 举个例子,当n=5,k=3时,你想得到组合{0,3,4}的下一个组合元素。索引i从位置2开始(位置2指向的值是4),然后索引左移直到位置0(位置0指向的值是0)。0位置的值增加到1,然后位置在它右边的所有值(3和4)都比左边的大1,因此得到结果{1,2,3}。
有了Successor函数还不够,你还需要ApplyTo函数接收组合元素:
{
if (strarr.Length != this.n)
throw new Exception("Bad array size");
string[] result = new string[this.k];
for (long i = 0; i < result.Length; ++i)
result[i] = strarr[this.data[i]];
return result;
}
在确认了字符串数组的长度正确后,我们创建了一个长度为k的result字符串数组,该数组为传入的数组的每个位置存储了引用。如果还不理解,就自己运行程序调试跟踪吧~~~
在创建了一个组合实例后,我们创建了一个字符串数组来保存组合结果。用一个while循环遍历所有的组合元素——直到Successor方法返回null,表示组合元素遍历完成——然后ApplyTo函数映射对应元素的值。
结 论
组合在规划和执行配置的测试中有着不可替代的作用,特别是在一些互动分析的分支领域。假如你需要在一台机器上测试多种浏览器和媒体播放器来安装你的产品,你想要你的系统从8种浏览器中选择3种安装,并从6个媒体播放器中选择2个安装,一共有多少种可能的配置?你能否用程序列举出所有的配置?本文的程序能够让你轻松得到结果:Choose(8,3)*Choose(6,2)=840,并且你可以列举出所有的组合类型。
组合在检查和测试执行路径时很有用。 我讲一个经典的执行路径分析的例子(这类问题经常在微软面试软件测试工程师时出现)。假设你正在开发一个游戏,玩家从有瓷砖地板的西南角房间进入,他们必须移动到房间的东北角,而要移动过去,必须通过把瓷砖向东或向北移动(换句话说,玩家必须移动向他们要去的方向,而不能回头)。如果房间很小——只有10个瓷砖能水平移动,6个瓷砖能竖直移动——共有多少种路径可供玩家选择?你能够列举出所有正确路径么?假定向东移动用英文字母E表示,向北用N,一种可能的路径是,先向东走到头,再向北走到头:
还有一种不同的走法:
显然,无论玩家怎么走,他都只会走16步,而且走的方式只有“E”和“非E”两种。你可以在脑海中构造一个16个连续的空格,你必须要在这16个空格中填充入10个“E”(因为剩下的必须填“N”)。所以,这个问题的答案便是Choose(16,10)=8080种可能的路径,你可以通过本片的代码轻松得到结果。
正如我之前所说,测试在软件开发中具有非常重要的作用,跟着我一起,你可以把这些优化加入在你的测试过程中。



