高考集训2 题解
本次考试喜提 0pts
犯了(我之前以为我从来不会犯得)文件错误
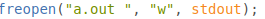
注意到多了一个空格
100pts ->(数组开小)->60pts->(文件打错)0pts
A.交通
同一个点出边和出边互斥, 入边和入边互斥,2-sat的思想建图即可(虽然我好像没学过2-sat)
注意一个边拆成了四个点,一个点有四条边,所以数组猛开就是了
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll MOD = 998244353;
const int N = 2e6+10, E = 2*N;
int n;
struct DSU{
int fa[N * 4];
void init(int len){
for(int i = 1; i <= len; ++i) fa[i] = i;
}
int find(int x){
return x == fa[x] ? x : fa[x] = find(fa[x]);
}
void merge(int x, int y){
x = find(x), y = find(y);
if(x < y) std::swap(x, y);
//大挂小
fa[x] = y;
}
}un;
bool sol[N * 4];
int change(int x){
//cerr<<"2"<<endl;
return x == 0 ? 1 : 0;
}
int id(int u, int cnt, bool in){
return u + cnt*n + in*2*n;
}
int plc(int e, bool out){
return e + out * 2 * n;
}
int cgplc(int e){
if(e > 2 * n) return e - 2 * n;
return e + 2 * n;
}
struct Graph{
struct edge{
int nxt, to;
}e[E];
int elen, head[N];
void inse(int frm, int to){
// cerr<<"ins"<<frm << " "<< to <<endl;
e[++elen] = {head[frm], to};
head[frm] = elen;
}
int st[N * 4];
// 0 : nothing 1 : true -1 : false
bool bfs(int s){
queue<int> q;
q.push(s);
//cerr<<"2"<<endl;
bool flg = true;
while(!q.empty()){
int u = q.front(); q.pop();
if(st[u] || st[cgplc(u)]) {
if(st[u] != 1 || st[cgplc(u)] != -1){
flg = false;break;
}
continue;
}
st[u] = 1, st[cgplc(u)] = -1;
for(int i = head[u]; i;i = e[i].nxt){
int v = e[i].to;
q.push(v);
}
}
q.push(s);
while(!q.empty()){
int u = q.front(); q.pop();
if(st[u] == 0) continue;
st[u] = st[cgplc(u)] = 0;
for(int i = head[u]; i;i = e[i].nxt){
int v = e[i].to;
q.push(v);
}
}
return flg;
}
void setsol(int s){
queue<int> q;
q.push(s);
while(!q.empty()){
int u = q.front(); q.pop();
if(sol[u]) continue;
sol[u] = sol[cgplc(u)] = true;
// cerr<<"seted"<<u<<" " << cgplc(u) <<endl;
for(int i = head[u]; i; i = e[i].nxt){
int v = e[i].to;
q.push(v);
}
}
}
}G;
void connect(int e1, int e2){
G.inse(plc(e1, true), plc(e2, false));
G.inse(plc(e2, true), plc(e1, false));
G.inse(plc(e1, false), plc(e2, true));
G.inse(plc(e2, false), plc(e1, true));
}
bool viso[N][2], visi[N][2];
struct q_t{
int u, v, eu, ev;
}que[2*N];
int main(){
freopen("a.in", "r", stdin);
freopen("a.out", "w", stdout);
cin >> n;
// cerr<<id(2, 1, true);
// cerr<<plc(1, true)<< " " << plc(3, false) << endl;
//u*1 ,u *2 : oute
//u*3, u*4 :ine
un.init(n*4);
for(int i = 1; i <= 2*n; ++i){
int u, v;
cin >> u >> v;
int eu = 0, ev = 0;
if(viso[u][eu]) eu = change(eu);
if(visi[v][ev]) ev = change(ev);
un.merge(id(u, eu, false), id(v, ev, true));
viso[u][eu] = visi[v][ev] = true;
que[i] = {u, v, eu, ev};
}
for(int i = 1; i <= 2*n; ++i){
int u = que[i].u, v = que[i].v, eu = que[i].eu, ev = que[i].ev;
// cerr<<u << " " << eu << " " << v << " " << ev << endl;
// cerr<<"num = " << id(u, eu, false) << " " << id(v, ev, true)<<endl;
}
//正:1~2*n 反:2n+1 ~ 4n
for(int i = 1; i <= 2*n; ++i){
int u = que[i].u, v = que[i].v, eu = que[i].eu, ev = que[i].ev;
int e1 = un.find(id(u, eu, false)), e2 = un.find(id(u, change(eu), false)),
e3 = un.find(id(v, ev, true)), e4 = un.find(id(v, change(ev), true));
// cerr<<e1 << " " << e2 << " " << e3 << " " << e4 << endl;
connect ( un.find(id(u, eu, false)), un.find(id(u, change(eu), false)));
connect ( un.find(id(v, ev, true)), un.find(id(v, change(ev), true)));
}
ll ans = 1;
// G.setsol(1);
// return 0;
for(int i = 1; i <= 2 * n; ++i){
ll tans = 0;
if(!sol[i]){
if(G.bfs(plc(i, true))){
++tans;
}
if(G.bfs(plc(i, false))){
++tans;
}
G.setsol(i);
ans = tans * ans % MOD;
}
}
cout<<ans<<endl;
return 0;
}
B .冒泡排序
此题操作之间有一些微妙的顺序,其实考场上看出来了但是没想明白
这是由于每种操作只能做一次导致的
操作顺序虽然是个DAG,但是是一条链状DAG,所以利用特殊性可以dp
\(f[i][j]\) 第 \(i\) 个操作在前\(i\)个操作里面的排名为\(j\)的方案数
using namespace std;
const int N = 5E3+10, TR = 8*N;
typedef long long ll;
const ll MOD = 1E9+7;
int n;
ll f[N][N];
ll sum[N];
int a[N];
int s[N];
struct segment_tree{
struct node{
int laz, val;
}tree[TR];
bool update(int rt, int val){
if(tree[rt].val != 0 && val != tree[rt].val) return false;
tree[rt].val = val;
tree[rt].laz = val;
return true;
}
void push_down(int rt){
if(tree[rt].laz){
update(rt<<1, tree[rt].laz);
update(rt<<1|1, tree[rt].laz);
tree[rt].laz =0 ;
}
}
bool modify(int rt, int l, int r, int s, int t, int v){
if(s > t) return true;
if(s <= l && r <= t){
return update(rt, v);
}
int mid = (l + r) >> 1;
push_down(rt);
bool flg = false;
// assert(s <= mid || t > mid);
if(s <= mid) flg = modify(rt<<1, l, mid, s, t, v);
if(t > mid) flg = modify(rt<<1|1, mid +1 , r, s, t, v) || flg;
// assert(flg == false);
return flg;
}
int query(int rt, int l, int r, int x){
if(l == r){
assert(l ==x);
return tree[rt].val;
}
int mid = (l + r) >> 1;
push_down(rt);
if(x <= mid)
return query(rt<<1, l, mid, x);
else return query(rt<<1|1, mid+1, r, x);
}
}segt;
int main(){
freopen("mp.in", "r", stdin);
freopen("mp.out", "w", stdout);
cin >> n;
for(int i = 1; i <= n; ++i){
cin >> a[i]; ++a[i];
if(a[i] == i){
cout << 0 << endl;
return 0;
}
if(a[i] < i){
if(!segt.modify(1, 1, n, a[i]+1, i-1, 1)){
// cerr<< "i = "<<i<<endl;
cout << 0 <<endl;
return 0;
}
// cerr<<a[i] + 1 << " " << i-1 << endl;
//val:相对priority, 越大越靠前
}else{
if(!segt.modify(1, 1, n, i+1, a[i]-1, -1)){
// cerr<<"i = "<<i << endl;
cout << 0 <<endl;
return 0;
}
}
}
for(int i = 1; i <= n-1; ++i){
s[i] = segt.query(1, 1, n, i);
}
for(int i = 1; i <= n-1; ++i){
cerr << s[i] << " " ;
}
cerr<<endl;
f[1][1] = 1;
for(int i = 2; i <= n-1; ++i){
// cerr<<"i = "<< i <<endl;
memset(sum,0, sizeof(sum));
for(int j = 1; j <= i; ++j){
sum[j] = (sum[j-1] + f[i-1][j] ) %MOD;
}
for(int j = 1; j <= i; ++j){
if(s[i] == 0){
f[i][j] = (sum[i-1] - sum[0] ) %MOD;
/*
for(int k = 1; k <= i-1; ++k){
f[i][j] = (f[i][j] + f[i-1][k])%MOD;
}*/
}
if(s[i] == 1){
f[i][j] = (sum[j-1] - sum[0] ) %MOD;
/*
for(int k = 1; k <= j-1; ++k){
f[i][j] = (f[i][j] + f[i-1][k])%MOD;
}*/
// cerr<<i <<" " <<j << " "<< f[i][j]<<endl;
}
if(s[i] == -1){
if(j-2 >= 0) f[i][j] = (sum[i-1] - sum[j-1] + MOD)%MOD;
else f[i][j] = sum[i-1];
/*
for(int k = j; k <= i-1; ++k){
f[i][j] = (f[i][j] + f[i-1][k])%MOD;
}*/
}
}
}
ll ans = 0;
for(int i = 1; i <= n-1; ++i){
ans = (ans + f[n-1][i])%MOD;
}
cout << ans << endl;
return 0;
}
C.矩阵
构造题,考试中一眼没看
有一个非常有趣的性质
由"GCC"定理得,若有解,则前两行与前两列为 \(0\) 时,整个矩阵必然为 \(0\)
GCC定理证明

如图,对于任意一个 \(3*3\) 矩形,无论进行什么操作,左上角的$黄色-红色 $与 右下角的 $黄色-红色 $之差永远不变
所以,对于一个有解矩阵,左上角的 \(黄色-红色\) = 右下角的 $黄色-红色 = 0 $(因为最终状态是全\(0\))
因此,对于一个有解矩阵,确定了这\(6\)个方块中的任意 \(5\)个就可以确定出来 另一个

因此,棕色的\(3*3\)方块为\(0\)可以得出红色方块为\(0\)
类似的,我们反复运用这个方法确定出来一行的方块为\(0\)


我们反复运用这个而方法可以确定更多的行为\(0\)直到填满整个矩阵
GCC定理得证

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e3+10, M = 1e3+10, K = 6000+100;
enum{OptLin = 1, OptCol = 2, OptSpe = 3};
ll a[N][M];
int n, m;
struct q_t{
int opt, k;
ll val;
}que[K];
int cnt;
void operation(int opt, int k, ll val){
if(opt == 1){
for(int i = 1; i <= m; ++i){
a[k][i] += val;
}
}else if(opt == 2){
for(int i = 1; i <= n; ++i){
a[i][k] += val;
}
}else{
int x1 = 1, x2 = 1-k;
int x = std::max(x1, x2);
for(int i = x, j = x + k; i <= n && j <= m; ++i, ++j){
a[i][j] += val;
}
}
}
void push(int opt, int k, ll val){
que[++cnt] = {opt, k, val};
operation(opt, k, val);
}
bool check(){
for(int i = 1; i <= n; ++i){
for(int j = 1; j <= m; ++j){
if(a[i][j] != 0) return false;
}
}
return true;
}
void prt(){
for(int i = 1; i <= n; ++i){
for(int j = 1; j <= m; ++j){
cerr<< a[i][j] << " ";
}
cerr<<endl;
}
}
int main(){
freopen("c.in", "r", stdin);
freopen("c.out", "w", stdout);
cin >> n >> m;
for(int i = 1; i <= n; ++i){
for(int j = 1; j <= m; ++j){
cin >> a[i][j];
}
}
if(n == 1){
cout << m << endl;
for(int j = 1; j <= m; ++j){
cout << 2 << " " << j << " " <<-a[1][j] <<endl;
}
return 0;
}
for(int j = m; j >= 1; --j){
push(OptCol, j, -a[1][j]);
push(OptSpe, j-2, -a[2][j]);
}
for(int i = 3; i <= n; ++i){
push(OptLin, i, -a[i][2]);
push(OptSpe, 1-i, -a[i][1]);
}
// prt();
if(!check()){
cout << -1 << endl;
return 0;
}
cout << cnt<< endl;
for(int i = 1; i <= cnt; ++i){
cout << que[i].opt << " " << que[i].k << " " << que[i].val << endl;
}
return 0;
}
D. 花瓶
刷新了我对斜率优化的认知
斜率优化应该考虑两个操作的优秀顺序,从而得出斜率柿子与枚举顺序, 注意除0错误可以转化为乘法
注意 \(\leq\)与\(<\)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 5E3+10;
int a[N], ord[N];
ll s[N];
ll f[N][N];
int n;
deque<int> q;
int main(){
freopen("d.in", "r", stdin);
freopen("d.out", "w", stdout);
ios::sync_with_stdio(false);
cin >> n;
for(int i = 1; i <= n; ++i){
cin >> a[i];
s[i] = s[i-1] + a[i];
ord[i] = i;
}
std::sort(ord, ord+1+n, [](int x, int y){return s[x] < s[y] ; });
memset(f, 0x80, sizeof(f));
for(int i = 0; i <= n; ++i){
f[i][0] = 0;
}
for(int j = 1; j <= n; ++j){
q.clear();
for(int k = 0; k <= n; ++k){
if(ord[k] >= j) continue;
int r = int(q.size()) -1;
while(q.size() >= 2 && (f[j][q[r]] - f[j][q[r-1]] ) * (s[ord[k]] - s[q[r-1]]) <= (f[j][ord[k]] - f[j][q[r-1]]) * (s[q[r]]- s[q[r-1]])) q.pop_back();
//防止分母为0
q.push_back(ord[k]);
}
for(int i = n; i >= 0; --i){
if(ord[i] <= j) continue;
int r = int(q.size()) - 1;
while(q.size() >= 2 && (s[ord[i]] - s[j]) * (s[q[1]] - s[q[0]]) <= (f[j][q[1]] - f[j][q[0]])) q.pop_front();
//to multi a minus number you have to change the sign
f[ord[i]][j] = std::max(f[ord[i]][j], f[j][q[0]] + (s[ord[i]] - s[j]) * (s[j]-s[q[0]]));
}
}
ll ans = 0;
for(int j = 0; j < n; ++j){
ans = std::max(ans, f[n][j]);
}
cout << ans << endl;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号