[复习]分块/莫队

首先广为人知的莫队复杂度证明：网上题解证明的大部分有bug,这里改进一下
总询问为$q$, 总大小为$n$
莫队复杂度证明：设块长为$S$，则共有$B := n/S$个块
首先考虑块内移动:
单个块考虑
右指针：单调递增，$O(n)$
左指针：每个询问最多移动块长，设第$i$块询问个数为$f(i)$即$S$ , $f(i)*S$
总复杂度：
右$B*n$
左$\sum_{i = 1}^{B}{f(i)*S}$ = $S*\sum_{i=1}^{B}{f(i)}$ = $S*q$
$n/S*n+S*q$ = $n^2/S+S*q$
然后考虑块间移动：
左:$2*S$
右:$O(n)$
总复杂度 $O（B*(S+n)）$ = $O(n^2/S+n)$
算法总复杂度
$O(n+2*n^2/S+S*q)$ = $O(n^2/S+S*q)$
对勾函数，当$S = \sqrt{n^2/m}$ = $\frac{n}{\sqrt{m}}$时候，总复杂度为$O(n\sqrt{m})$
接下来是待修改莫队
设块长为$S$,共有$B := n/S$个块
分开考虑每个指针的移动
时间指针：每个右端点块会最多移动$q$次，每个左端点块有B个右端点块，所以共有$B^2$个右端点块了，$O({(\frac{n}{s})}^2*q)$
左右指针与刚才的分析一致
所以是$O(S*q+\frac{n^2}{S}+{(\frac{n}{S})}^2*q)$

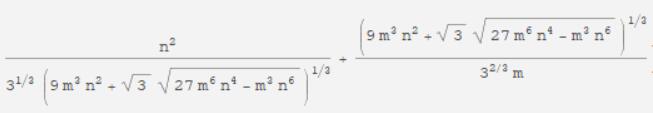
根据ouuan dalao的博客， S取值为这个时函数有最小值
然后当$q$与$n$同阶时候小值，为$O(n^{\frac{5}{3}})$
注意点:
1.求块长时候让$S = ceil(n/sqrt(m))$
2.求bel数组时候$bel[i] = ceil(1.0*i/S)$
3.分块求L数组与R数组时候 要把最后一个块的R赋值成n
4.注意运算顺序，不要用$a[++i] = node(i,a,b)$这样的操作，可能先算++i再调用构造函数，也可能先用构造函数再用++i, 所以用逗号表达式一劳永逸++i, a[i] = node(i, a, b)即可
5.注意原始信息和维护信息的区别，比如sort块内的时候不要干扰原始信息

莫队常用技巧：
奇偶性排序：
排序函数里面这么写

if(pos[a.l] != pos[b.l]) pos[a.l]<pos[b.l]
else return pos[a.l]&1?a.r<b.r:a.r>b.r;

大概就是减少右端点移动
回滚莫队:
给出一个长度为n的排列P(P1,P2,...Pn)，以及m个询问。每次询问某个区间[l,r]中，最长的值域 连续段长度。
从上到下一次
做法一：权值线段树+普通莫队，但是复杂度过大，是$O(logn*n\sqrt(n))$的
做法二（我的做法):权值并查集，求把连续段整成siz，复杂度$O(\sqrt{n}log(n)q+n\sqrt{n})$
做法三：题解做法，求出值域上向左向右延伸的最大长度
参考资料:
$\large\boxed{\textsf{ouuun的博客}}$