三维变换之斜投影、透视投影
编译器:VS2013
原理:依旧是矩阵相乘,只要求得矩阵就可以很方便的求出结果
注意!注意!注意!
楼主数学学得不好,齐次坐标这里没好好听,齐次坐标的第四个坐标值一直为1,楼主懵逼的也按物体坐标等比例放大导致错误调了两天
错误:
1 int a[8][4] = { 0, 0, 0, 200, 200, 0, 0,200, 200, 200, 0,200, 0, 200, 0,200, 0, 0, 200,200, 200, 0, 200,200, 200, 200, 200,200, 0, 200, 200,200};
正确:
1 int a[8][4] = { 0, 0, 0, 1, 200, 0, 0, 1, 200, 200, 0, 1, 0, 200, 0, 1, 0, 0, 200, 1, 200, 0, 200, 1, 200, 200, 200, 1, 0, 200, 200, 1 };
主函数块
1 #include "stdafx.h" 2 #include<stdio.h> 3 #include"graphics.h" 4 #include<stdlib.h> 5 #include<math.h> 6 7 #define PI 3.14159 8 9 //函数声明 10 void apoint(int a[][4]);//一点透视 11 void oblique2_30(int a[][4]);//斜二测45° 12 void oblique2_45(int a[][4]);//斜二测30° 13 void twopoint(int a[][4]);//两点透视 14 void threepoint(int a[][4]);//三点透视 15 void putline(double b[][4]);//画线函数 16 17 int main() 18 { 19 int gdriver = DETECT, gmove; 20 int a[8][4] = { 0, 0, 0, 1, 200, 0, 0, 1, 200, 200, 0, 1, 0, 200, 0, 1, 0, 0, 200, 1, 200, 0, 200, 1, 200, 200, 200, 1, 0, 200, 200, 1 }; 21 22 initgraph(&gdriver, &gmove, ""); 23 setcolor(YELLOW); 24 25 apoint(a);//一点透视 26 //oblique2_30(a);//斜二测30° 27 //oblique2_45(a);//斜二测45° 28 //twopoint(a);//两点透视 29 //threepoint(a);//三点透视 30 31 system("pause"); 32 33 closegraph(); 34 35 return 0; 36 }
一点透视:
1 //一点透视 2 void apoint(int a[][4]) 3 { 4 double k = 160, m = 220, n = 400, d = 500,b[8][4]; 5 int i; 6 7 for (i = 0; i < 8; i++) 8 { 9 b[i][3] = (d + n + a[i][2]) / d*1.0;//其次变换 10 b[i][0] = (a[i][0] + k) / b[i][3]*1.0;//x变换 11 b[i][1] = (a[i][1] + m) / b[i][3]*1.0;//y变换 12 b[i][2] = 0;//z变换 13 b[i][3] = 1;//齐次坐标赋1 14 } 15 16 putline(b);//画线函数
画线函数
1 void putline(double b[][4]) 2 { 3 int i; 4 5 //小图层 6 for (i = 0; i < 3; i++) 7 line(b[i][0], b[i][1], b[i + 1][0], b[i + 1][1]); 8 9 //小图层尾连接 10 line(b[3][0], b[3][1], b[0][0], b[0][1]); 11 12 //大图层 13 for (i = 4; i < 7; i++) 14 line(b[i][0], b[i][1], b[i + 1][0], b[i + 1][1]); 15 16 //大图层首尾连接 17 line(b[4][0], b[4][1], b[7][0], b[7][1]); 18 19 //大小图层连接 20 for (i = 0; i < 4; i++) 21 line(b[i][0], b[i][1], b[i + 4][0], b[i + 4][1]); 22 }

二点透视
1 //两点透视 2 void twopoint(int a[][4]) 3 { 4 double p = 0.002, r = 0.002, A = PI / 6.0, k = 150, n = 30, m = 50; 5 //二维数组c为转换矩阵 6 double b[8][4] = { 0 }; 7 //转换矩阵 8 double c[4][4] = { { cos(A), 0, 0, p*cos(A) - r*sin(A) }, { 0, 1, 0, 0 }, { sin(A), 0, 0, p*sin(A) + r*cos(A) }, { k*cos(A) + n*sin(A), m, 0, p*(k*cos(A) + n*sin(A)) + r*(n*cos(A) - k*sin(A)) + 1 } }; 9 int i, j, x; 10 11 //矩阵相乘 12 for (i = 0; i < 8; i++) 13 for (j = 0; j < 4; j++) 14 for (x = 0; x < 4; x++) 15 b[i][j] += a[i][x] * c[x][j]; 16 17 for (i = 0; i < 8; i++) 18 for (j = 0; j < 4; j++) 19 { 20 b[i][j] /= b[i][3];//使齐次坐标变为1 21 b[i][j] = (int)b[i][j];//取整 22 } 23 24 putline(b);//画线函数 25 }
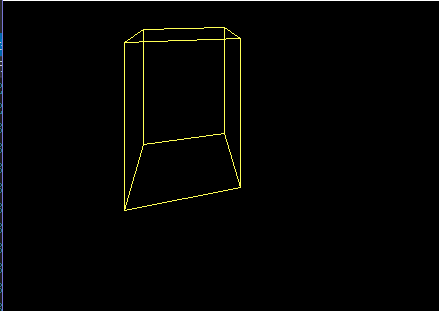
三点透视
1 //三点透视 2 void threepoint(int a[][4]) 3 { 4 double p = 0.0015,q=0.0015, r = 0.0015, A = PI / 6.0,B=PI/45, k = 150, n = 30, m = 30; 5 //二维数组c为转换矩阵 6 double b[8][4] = { 0 }; 7 //转换矩阵 8 double c[4][4] = { { cos(A),sin(A)*sin(B),0,p }, { 0,cos(B),0,q }, { sin(A),-cos(A)*sin(B),0,r }, { k*cos(A)+n*sin(A), m*cos(B)+sin(B)*(k*sin(B)-n*cos(A)),0,k*p+m*q+n*r} }; 9 int i, j, x; 10 11 //矩阵相乘 12 for (i = 0; i < 8; i++) 13 for (j = 0; j < 4; j++) 14 for (x = 0; x < 4; x++) 15 b[i][j] += a[i][x] * c[x][j]; 16 17 for (i = 0; i < 8; i++) 18 for (j = 0; j < 4; j++) 19 { 20 b[i][j] /= b[i][3];//使齐次坐标变为1 21 b[i][j] = (int)b[i][j];//取整 22 } 23 24 putline(b);//画线函数,括号内强制转换成int 25 }

斜二测30°
1 //斜二测30° 2 void oblique2_45(int a[][4]) 3 { 4 double b[8][4]; 5 int i; 6 7 for (i = 0; i < 8; i++) 8 { 9 b[i][0] = a[i][0] + a[i][2] * cos(PI / 4)*sqrt(5.0) / 5 * 1.0;//x变换 10 b[i][1] = a[i][1] + a[i][2] * sin(PI / 4)*sqrt(5.0) / 5 * 2.0;//y变换 11 b[i][2] = 0;//z变换 12 b[i][3] = 1;//齐次坐标变换 13 } 14 15 putline(b);//画线函数 16 }

斜二测45°
1 //斜二测45° 2 void oblique2_30(int a[][4]) 3 { 4 double b[8][4]; 5 int i; 6 7 for (i = 0; i < 8; i++) 8 { 9 b[i][0] = a[i][0] + a[i][2] * cos(PI / 6)*sqrt(5.0) / 5 * 1.0;//x变换 10 b[i][1] = a[i][1] + a[i][2] * sin(PI / 6)*sqrt(5.0) / 5 * 2.0;//y变换 11 b[i][2] = 0;//z变换 12 b[i][3] = 1;//齐次坐标变换 13 } 14 15 putline(b);//画线函数 16 }




