盛最多水的容器
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例 1:
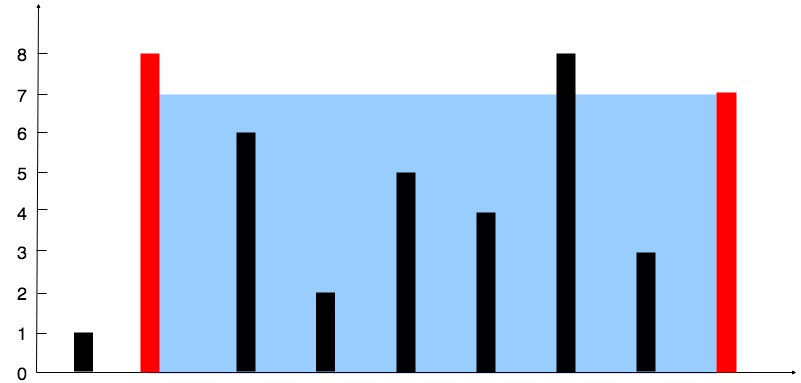
输入:[1,8,6,2,5,4,8,3,7] 输出:49 解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1] 输出:1
提示:

解答:
分析:1)暴力法:
public static int getMax(int[] args){
int max = 0;
for (int i=0; i < args.length-1; i++){
for (int j =i+1; j < args.length;j++){
int temp = Math.min(args[i],args[j])*(j-i);
if (max < temp){
max = temp;
}
}
}
return max;
}
简单地用例都可以通过,但是当数组很大的时候,就会出现时间复杂度超时问题
2)寻找简单算法分析

public static int getMaxArea(int[] height){
int max=0; int i=0; int j = height.length-1;
while (i < j){
if (height[i] > height[j]){
int temp = height[j]*(j-i);
if (temp>max){
max = temp;
}
--j;
}else {
int temp = height[i]*(j-i);
if (temp > max){
max = temp;
}
++i;
}
}
return max;
}
或者
public static int getMaxArea22(int[] height){
int max=0; int i=0; int j = height.length-1;
while (i < j){
int temp = Math.min(height[i],height[j])*(j-i);
max = Math.max(temp, max);
if (height[i] > height[j]){
--j;
}else {
++i;
}
}
return max;
}
或者
public static int getMaxRes(int[] height){
int max=0; int i=0; int j = height.length-1;
while (i < j){
max = height[i] < height[j] ? Math.max(max, height[i++]*(j-i)): Math.max(max, height[j--]*(j-i));
}
return max;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号