【ICPC2019上海站】H - Tree Partition

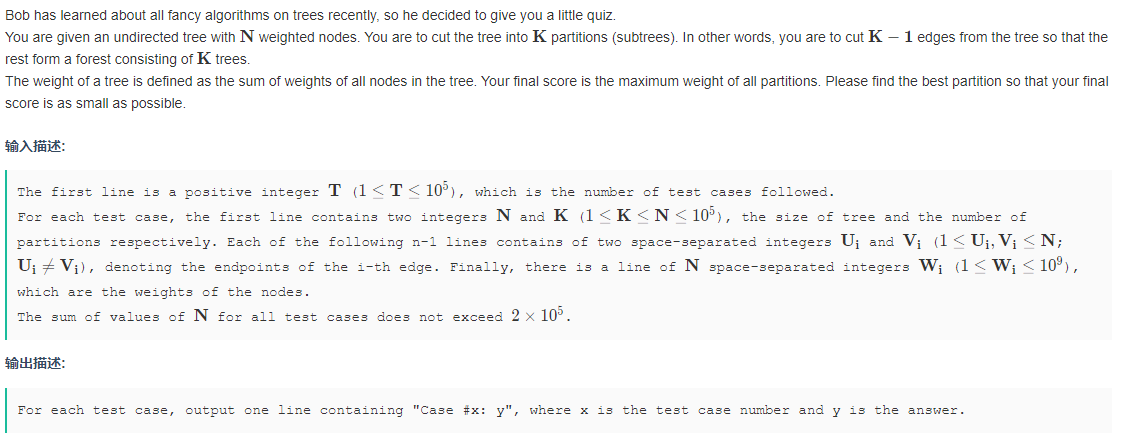
原题：

 

 翻译：

给你一个点权无根树，要你切掉k-1条边把它切成k个子树，要求切完后子树的点权和的最大值最小

 

一看最大值最小，那必然是二分

问题转化为给你一个值，问你能否把这个树切成不多于k个子树，且每个子树点权和不超过给的值

贪心1：

叶子一定选

贪心2：

如果某个点的子树全能装得下，那一定一把梭

证明：

假设子树的某个子树（也就是孙树）不选，可以使得子树的爸爸多塞两个兄树进去，那么其实完全可以把子树和爸爸的边切掉，让爸爸带两个兄弟跑路，儿子带着孙子，这样答案是没变的，但是爸爸的负担反而轻了，以后还可能比爸爸拖着除了孙树的所有子孙优

那么现在需要考虑子树不能全装的情况

然后我在这一步了比较久，要往下继续贪心不能光靠猜想，还有必要研究性质

性质：

爸爸要么拖几个儿子的子树，要么自己跑路，如果爸爸跑路，那么儿子都跟祖先没啥关系了

这个很好理解，但是必须要想到

想到这个性质之后，就可以继续贪心

贪心3：

每个爸爸的子树（去掉已经打包带走的点之后的剩余部分）按大小排序，然后从小到大枚举，尽可能和爸爸合并

因为爸爸反正都要选，能拖几个儿子就拖几个儿子，优先拖小儿子的最优性易证

这样这道题就做完了

具体实现还不是很直接，有一些需要仔细想想的地方，在代码里标出来了

 

代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
using ll=long long int;
const ll oo=1000000007;
struct edg{int nxt,y;}e[210000];  int lk[110000],ltp=0;
void ist(int x,int y){
    e[++ltp]=(edg){lk[x],y};  lk[x]=ltp;
    e[++ltp]=(edg){lk[y],x};  lk[y]=ltp;
}
int n,m,a[110000];
ll q[110000];  int hd=0;
ll f[110000];
ll dfs(int x,int y,ll z){
    if(a[x]>z)  return oo;  //注意此处int会溢出
    f[x]=a[x];
    ll cnt=1;
    for(int i=lk[x];i;i=e[i].nxt)if(e[i].y!=y){
        cnt+=dfs(e[i].y,x,z);  //易误点，需要想清楚
        //q[++hd]=f[e[i].y];
    }
    for(int i=lk[x];i;i=e[i].nxt)if(e[i].y!=y)
        q[++hd]=f[e[i].y];
    sort(q+1,q+hd+1);
    for(int i=1;i<=hd && f[x]+q[i]<=z;++i){
        f[x]+=q[i];
        cnt--;  //易误点，需要想清楚
    }
    for(int i=lk[x];i;i=e[i].nxt)if(e[i].y!=y)
        hd--;  //易错点！！！
    return cnt;
}
bool chc(ll x){
    return dfs(1,0,x)<=m;
}
ll bsc(){
    ll l=0,r=oo*oo,md;
    while(l+1<r){
        md=(l+r)>>1;
        (chc(md) ? r : l)=md;
    }
    return chc(l) ? l : r;
}
void prvs(){
    for(int i=1;i<=n;++i)  lk[i]=0;
    ltp=0;
    for(int i=1;i<=n;++i)  f[i]=0;
}
int main(){
    int T;  cin>>T;
    for(int t=1;t<=T;++t){
        scanf("%d%d",&n,&m);
        prvs();
        int l,r;
        for(int i=1;i<n;++i){
            scanf("%d%d",&l,&r);
            ist(l,r);
        }
        for(int i=1;i<=n;++i)  scanf("%d",&a[i]);
        printf("Case #%d: %lld\n",t,bsc());
    }
    return 0;
}