【HAOI2007】反素数

原题：

 

 

 

 

 

 

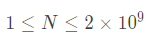
最开始觉得要么是个公式，要么是个结论

结果研究了半天越推越奇怪，这不会是个dp吧……

先按下不表，研究性质还是可以得到很有用的信息的

1.结论，令h(x)表示因子个数为x的反质数，则h(x)是单调的（h函数的定义域并不是正整数，在有值的地方是单调的）

这个结论看上去很显然，但是它传递出一个关键的信息：找出最大的h(x)等价于找出最大的x

2.如果h(x)的质因子幂之积为2^k1*3^k2*5^k3*...（k可以为0），那么x=(k1+1)*(k2+1)*(k3+1)*...

想到这里就可以开始DP了

接下来只需令f[i]表示因子个数为i的最小的数，那么由性质2可以很轻松地进行转移

最后只需从高到低扫描f[i]，取出不大于n的最大值即可，这样做的正确性已经由性质1保证

 

代码：（写代码的时候思路还不是很清晰所以代码比较丑）

#include<iostream>
#include<cstdio>
#define LL long long
using namespace std;
const int oo=2000000007;
int n;
LL f[2][5100];
int pr[110000],pt=0;
int pf[110000];
void gtp(){
    for(int i=2;i<=100000;++i){
        if(pf[i]==0)  pr[++pt]=i;
        for(int j=1;j<=pt && pr[j]*i<=100000;++j){
            pf[i*pr[j]]=1;
            if(i%pr[j]==0)  break;
        }
    }
}
int main(){
    gtp();
    for(int i=1;i<=5000;++i){
        f[0][i]=oo;
        f[1][i]=oo;
    }
    scanf("%d",&n);
    f[0][1]=1;
    for(int i=1;i<=5000;++i){
        LL bwl=1;
        for(int j=0;;++j){
            for(int k=1;k<=5000;++k)if(k*(j+1)<=5000)
                f[i&1][k*(j+1)]=min(f[i&1][k*(j+1)],f[i&1^1][k]*bwl);
            bwl*=pr[i];
            if(bwl>n)  break;
        }
    }
    //for(int i=1;i<=20;++i)  cout<<f[1000][i]<<" ";
    //cout<<endl;
    for(int i=5000;i>=1;--i)if(f[0][i]<=n){
        printf("%lld\n",f[0][i]);
        break;
    }
    return 0;
}