【洛谷1044】栈
原题：
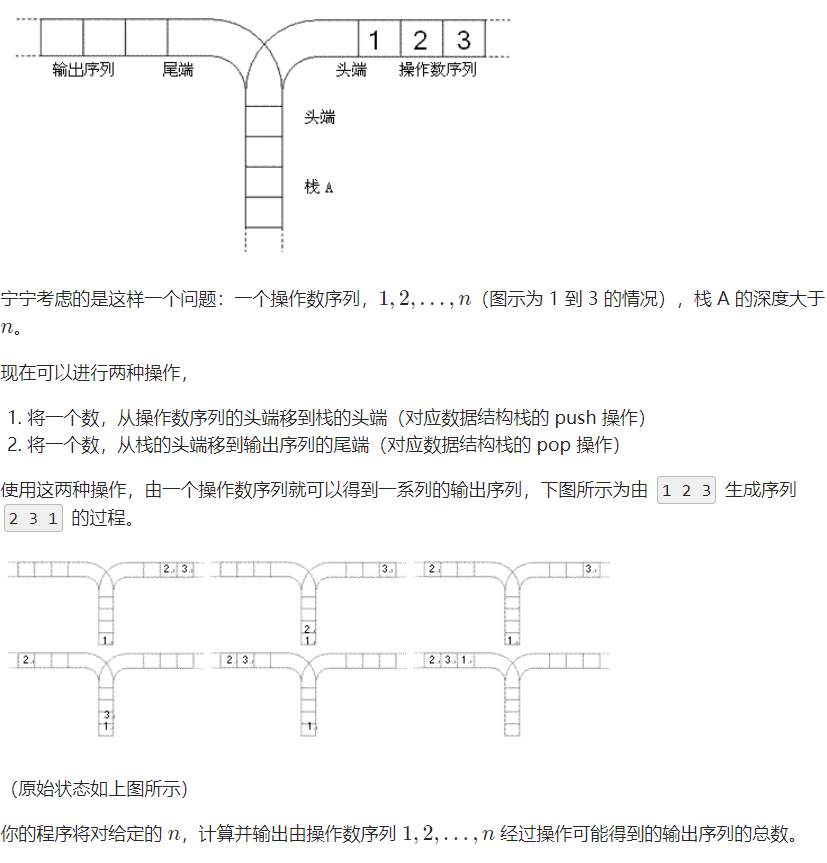
n<=18
性质 1 ：
观察发现，栈里的数的顺序一定等同它们在原序列的顺序
这个易证
这道题的原序列是递增的，所以栈里的数列也是递增的
因此可以设计状态，f [ i ] [ j ] 表示原序列还有 i 个数，栈内数的集合为 j（ j 是二进制压位数）的出栈数列方案数
n 很小，二进制压位就可以做了
但是实际上这道题还有更简单的做法，f [ i ] [ j ] 表示 i 个数没进过栈，j 个数在栈里的方案数
这个做法正确是因为
性质 2 ：
对于同一个初始序列，且初始序列中的数各不相同，压栈弹栈的操作序列与最终的结果序列是意义对应的
即不存在两种不同的操作序列，使得它们排序的结果相同
证明思路：
对于一个操作序列 s ，以及一个出栈序列 t ，尝试找出另一个操作序列，使得出栈序列等于 t
对于 t 中第一个数，由于本题中只能栈前进栈后出，所以若想让出栈序列第一个数和 t 的第一个数相等
必须执行和 s 对应部分相同的操作
剩余部分容易由归纳法类似证明
第三种做法是使用卡塔兰数
洛谷题解第一个讲得很好很清楚，我就不再造轮子了
其实是之前根本不会卡塔兰数，这里学习一个 =。=
代码：
1 #include<iostream> 2 #include<cstdio> 3 using namespace std; 4 int f[19][262144]; 5 int n; 6 int main(){ 7 cin>>n; 8 f[0][0]=1; 9 for(int i=0;i<=n;++i)for(int j=(1<<n)-1;j>=0;--j)if(f[i][j]){ 10 if(i!=n){ 11 f[i+1][j|(1<<i)]+=f[i][j]; 12 } 13 if(j!=0){ 14 int k=0; 15 for(k=0;k<n;++k)if(j&(1<<k)) break; 16 f[i][j^(1<<k)]+=f[i][j]; 17 } 18 } 19 cout<<f[n][0]<<endl; 20 return 0; 21 }
UPD：
2020.9.26发现以前写得有点小问题，放一下更严谨的给洛谷写的ppt里关于这题的解法
