结论和典例集合

 

O 用kmp判断字符串循环节

如果3*next[n]>=2*n，那么最大循环节长度为n-nxt[n]，循环节个数为n/(n-nxt[n])

特判：如果n是偶数且nxt[n]==n/2，那么循环节长度为n/2

O Pólya定理

 

O 所以用 m 种颜色给 n 元环染色的方案数为：

O 给一堆分数，把其中某些分数的分子和分母分别加起来得到一个新分数，新分数的最大值是原来分数中最大的分数

因为若两个分数a和b满足a<b，则a<=a+b<=b

同理，新的分数最小值是原来分数中最小的分数

O 每次给区间[i,i+n-1]里的数分别加上1,2,...,n，最后求每个数的值

f[i]表示第i个数上有i个要加的序列，g[i]表示要加到i上的值

操作的时候f[i]++，g[i]+=n，f[i+n]--
求值的时候f[i]+=f[i-1]，g[i]+=g[i-1]-f[i-1]

如果是递减序列同理，递增递减结合就可以求每个字符属于的回文子串的个数

O 错位排序方案数

f(n)=(n-1)*[f(n-1)+f(n-2)]

f(0)=1,f(1)=0,f(2)=1
注意f(0)=1不是0

O 卡塔兰数的四种求法

h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)*h(0) (n>=2)

h(n)=h(n-1)*(4*n-2)/(n+1)

h(n)=C(2n,n)/(n+1) (n=0,1,2,...)

h(n)=c(2n,n)-c(2n,n-1) (n=0,1,2,...)

O 栈排序的结果数

注意这里的栈排序只能从栈前进栈后出，否则什么序列都造得出来

而且要求初始序列不能有重复元素，否则又要麻烦一些

可以用卡塔兰数递推，洛谷某个题解写得很好很清楚

O 栈排序的性质

对于同一个初始序列，且初始序列中的数各不相同，压栈弹栈的操作序列与最终的结果序列是一一对应的

即不存在两种不同的操作序列，使得它们排序的结果相同

所以求栈排序的结果数也可以用f[i][j]递推，i表示还剩几个数，j表示栈里几个数

O O(n)求1~n的逆元

直接费马小定理可能被卡常

推一个结论：

 所以 f [ i ] = ( p - p / i ) * f [ p % i ] % p

O 分组并查集

给每个点拆点，每有一个属性就拆一个点，然后相同属性的分为一组

如果要载入组间关系，就合并两个组的点，如果载入组内关系就合并组内的

例题：【NOI2001】食物链

分组并查集，给每个动物拆ABC三个点，相同字母的分一组

 如果是吃的关系，就对A到B、B到C、C到A三种跨组关系都合并，如果是相等的关系，就三个组内合并

这样若组间的点位于同一集合，就说明存在吃的关系，如果组内的点位于同一集合，就说明存在相等的关系

两个动物的关系只有A吃B，B吃A，A等于B三种

要判断某种关系是否存在，只需判断剩下两个关系是否存在，如果存在就表示冲突

如果三种关系都不存在就表示不知道

O dilworth定理

对于一个偏序集，最少链划分等于最长反链长度

序列的最少下降划分等于最长不下降子序列长度（注意不下降是类似递增的而不是类似递减的）

O 整数分拆

递推公式：

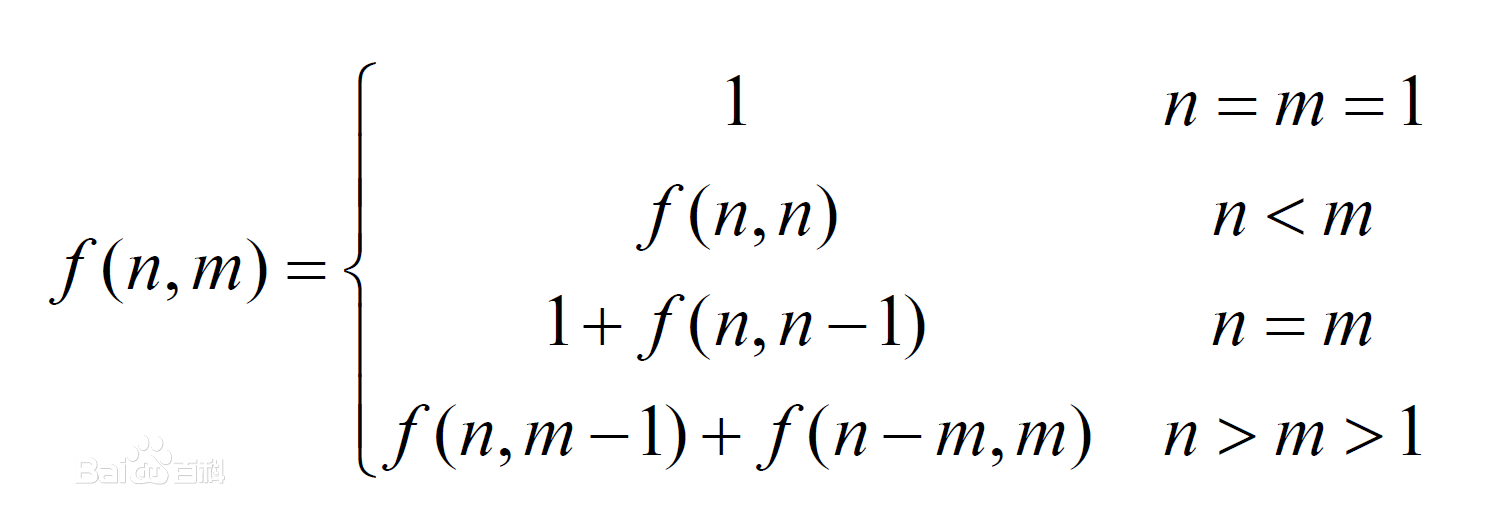
O 最小二分子图

二分答案，然后黑白染色

O 最长公共子序列

注意子序列特性，令c[i]表示a[i]在b中的位置，那么问题转化为对c求最长不下降子序列问题

O 最长不下降子序列

令g[i]为长度为i的不下降子序列里最后一个数最小是多少，显然g[i]随i递增

那么如果当前数大于所有的g，就让最大长度+1，把当前数放进去，否则二分找到第一个大于此数的g，然后替换他

二分方法：(g[md]<=x ? l : r)=md

O 最优比率生成树：

令原图为S，λ=a(x)/b(x)，其中a(x)表示子图x的a权之和，λ*=a(x*)/b(x*)为λ的最优值，则有0=a(x*)-λb(x*)

不妨设g(λ)=max{x⊆S | a(x)-λb(x)}，则g(λ)是单调递减函数，且g(λ*)=0

 

结论题：

O F(x)为x中1的个数，满足∑_0^x F(i)=x的最大数为1111111110