【NOIP2016】换教室

以前感觉很难不会的题，现在随便就做了呢 =w=

原题：

 

 

 

 

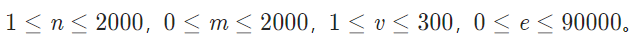
最初想法，f[i][j][k]表示第i节课，在第j个教室（j=1或0），用了k次机会

能想出这个状态就说明对期望和决策的理解不够。。。

把所在教室表示出来表面上看是表示出了状态，但是实际上期望是有不确定性的，如果把所在的点明确地表示出来就消除了这种不确定性

正确做法是用j=1或0表示是否选择换，即用决策表示状态

因为请求之间是相互独立的，所以可以直接用p[i]和p[i-1]来控制先后两个教室

如果不懂控制的意思，可以看如下详解

先考虑简单的情况，前后都不选

那么f[i][0][k]=min(f[i][0][k],f[i-1][0][k]+d[a[i][0]][a[i-1][0]])，其中d[i][j]表示i和j之间距离，a[i][0]表示原教室编号，a[i][1]表示换教室编号

如果前边选呢

f[i][0][k]=min(f[i][0][k],f[i-1][1][k]+d[a[i][0]][a[i-1][1]]*p[i-1]+d[a[i][0]][a[i-1][0]]*(1-p[i-1]))，其中d[i][j]表示i和j之间的距离，p[i]表示第i节申请成功的概率

这里就是所谓的用p[i-1]控制前边的教室

为什么f[i-1][1][k]能直接加而不乘概率呢

注意到，这个公式本来应该是p[i-1]*(第i-1节在a[i][1]的期望值+d[a[i-1][1]][a[i][0]])+(1-p[i-1])*(第i-1节在a[i][0]的期望值+d[a[i-1][0]][a[i][0]])

然后我们可以发现p[i-1]*第i-1节在a[i][1]的期望值+(1-p[i-1])*第i-1节在a[i][0]的期望值正是第i-1节选择申请的期望值

所以把这两项合并，就得到上述公式

这里需要注意理清期望的意义

对于其他两种情况同理

f[i][1][k]=min(f[i][1][k],f[i-1][0][k-1]+d[a[i][1]][a[i-1][0]]*p[i]+d[a[i][0]][a[i-1][0]]*(1-p[i]));

f[i][1][k]=min(f[i][1][k],f[i-1][1][k-1]
+d[a[i][1]][a[i-1][1]]*p[i]*p[i-1]
+d[a[i][1]][a[i-1][0]]*p[i]*(1-p[i-1])
+d[a[i][0]][a[i-1][1]]*(1-p[i])*p[i-1]
+d[a[i][0]][a[i-1][0]]*(1-p[i])*(1-p[i-1]));

还挺有规律的

 

代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
const int oo=1000000007;
int rd(){int z=0,mk=1;  char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')mk=-1;  ch=getchar();}
    while(ch>='0'&&ch<='9'){z=(z<<3)+(z<<1)+ch-'0';  ch=getchar();}
    return z*mk;
}
int n,o,m,c,a[2100][2];
int e[310][310];
double p[2100];
double f[2100][2][2100];
void flyd(){
    for(int k=1;k<=m;++k)for(int i=1;i<=m;++i)for(int j=1;j<=m;++j)
        e[i][j]=min(e[i][j],e[i][k]+e[k][j]);
}
void prvs(){
    for(int i=1;i<=m;++i){
        e[i][i]=0;
        for(int j=i+1;j<=m;++j)
            e[i][j]=oo,e[j][i]=oo;
    }
    for(int i=1;i<=n;++i)for(int j=0;j<=1;++j)
        for(int k=0;k<=o;++k)  f[i][j][k]=oo;
}
int main(){
    //freopen("ddd.in","r",stdin);
    cin>>n>>o>>m>>c;  prvs();
    for(int i=1;i<=n;++i)  a[i][0]=rd();
    for(int i=1;i<=n;++i)  a[i][1]=rd();
    for(int i=1;i<=n;++i)  scanf("%lf",&p[i]);
    int l,r,mk;
    while(c --> 0){
        l=rd(),r=rd(),mk=rd();
        e[l][r]=min(e[l][r],mk);
        e[r][l]=min(e[r][l],mk);
    }
    flyd();
    f[1][0][0]=0,f[1][1][1]=0;
    for(int i=2;i<=n;++i)for(int k=0;k<=o;++k){
        f[i][0][k]=min(f[i][0][k],f[i-1][0][k]
                +e[a[i][0]][a[i-1][0]]);
        f[i][0][k]=min(f[i][0][k],f[i-1][1][k]
                +e[a[i][0]][a[i-1][1]]*p[i-1]
                +e[a[i][0]][a[i-1][0]]*(1-p[i-1]));
        if(k){
            f[i][1][k]=min(f[i][1][k],f[i-1][0][k-1]
                    +e[a[i][1]][a[i-1][0]]*p[i]
                    +e[a[i][0]][a[i-1][0]]*(1-p[i]));
            f[i][1][k]=min(f[i][1][k],f[i-1][1][k-1]
                    +e[a[i][1]][a[i-1][1]]*p[i]*p[i-1]
                    +e[a[i][1]][a[i-1][0]]*p[i]*(1-p[i-1])
                    +e[a[i][0]][a[i-1][1]]*(1-p[i])*p[i-1]
                    +e[a[i][0]][a[i-1][0]]*(1-p[i])*(1-p[i-1]));
        }
    }
    double ans=oo;
    for(int i=0;i<=o;++i){
        ans=min(ans,f[n][0][i]);
        ans=min(ans,f[n][1][i]);
    }
    printf("%.2lf\n",ans);
    return 0;
}