【2019中国大学生程序设计竞赛-女生专场】C - Function

原题

 

 

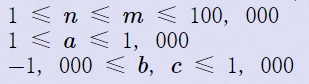
韦神提供的思路orz

首先一个显然的性质，所有的c可以提出来，方程变成ax^2+bx的形式

因为x的值是离散的，而m的值又不大

所以一开始让x都为1（注意！x是正整数），然后每次挑一个x让他加一

这样做怎么保证正确？

注意二次函数的性质，由于a>=1，当x递增时斜率，函数值的变化量是递增的

可以贪一个

每次去变化率最小的那个方程，让它的x加一

现在不取，后边也不会更优，所以正确

变化率相同时并不需要比较函数形状

因为由变化率递增的性质，就算取了较坏的函数，下一步还是取较好函数的相同变化量，然后再下一步必定会取到较好函数

 

代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
#define LL long long
int rd(){int z=0,mk=1;  char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')mk=-1;  ch=getchar();}
    while(ch>='0'&&ch<='9'){z=(z<<3)+(z<<1)+ch-'0';  ch=getchar();}
    return z*mk;
}
struct nds{LL x;  int y;}hp[110000];  int sz=0;
int n,m;
LL a[110000],b[110000],c[110000];
int d[110000];
LL cclt(LL x,int y){
    return x*x*a[y]+x*b[y];
}
void ist(nds x){
    hp[++sz]=x;
    for(int i=sz;i>1 && hp[i].x<hp[i>>1].x;i>>=1)  swap(hp[i],hp[i>>1]);
}
void pp(){
    swap(hp[1],hp[sz--]);
    for(int i=1;;){
        int mn=hp[i].x,mnid=i;
        if((i<<1)<=sz && hp[i<<1].x<mn)  mn=hp[i<<1].x,mnid=(i<<1);
        if((i<<1|1)<=sz && hp[i<<1|1].x<mn)  mn=hp[i<<1|1].x,mnid=(i<<1|1);
        if(i==mnid)  break;
        swap(hp[i],hp[mnid]);
        i=mnid;
    }
}
void prvs(){
    sz=0;
}
int main(){
    //freopen("ddd.in","r",stdin);
    while(scanf("%d%d",&n,&m)!=EOF){
        prvs();
        for(int i=1;i<=n;++i)  a[i]=rd(),b[i]=rd(),c[i]=rd();
        LL bwl=0;
        for(int i=1;i<=n;++i){
            d[i]=1;
            ist((nds){cclt(d[i]+1,i)-cclt(d[i],i),i});
            bwl+=cclt(d[i],i)+c[i];
        }
        for(int i=n+1;i<=m;++i){
            LL mn=hp[1].x;  int mnid=hp[1].y;
            ++d[mnid];
            pp();
            ist((nds){cclt(d[mnid]+1,mnid)-cclt(d[mnid],mnid),mnid});
            bwl+=mn;
        }
        printf("%lld\n",bwl);
    }
    return 0;
}