中国剩余定理(crt)和扩展中国剩余定理(excrt)
数论守门员二号 =。=
中国剩余定理:
1.一次同余方程组:
一次同余方程组是指形如x≡ai(mod mi) (i=1,2,…,k)的同余方程构成的组
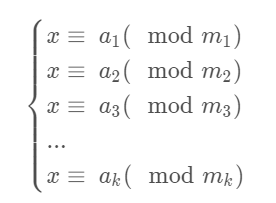
中国剩余定理的主要用途是解一次同余方程组,其中m1,m2,...,mk互质
2.中国剩余定理:
令M=m1*m2*...*mk(即所有m的lcm)
ti为同余方程M/mi*ti≡1(mod mi)的最小正整数解
则存在解x=∑ai*M/mi*ti
通解为x+i*M
最小非负整数解为(x%M+M)%M
(我承认这段是抄的orz
原文看起来更方便:https://blog.csdn.net/niiick/article/details/80229217)
M/mi*ti≡1(mod mi)可转化为M/mi*ti+mi*y=1,然后用exgcd求ti
其中gcd(M/mi, mi)=1,意义为方程组一定有解
3.证明:
对于第k个方程
①当i≠k时,有mk|M/mi,即ai*M/mi*ti≡0(mod mk)
②当i=k时,有M/mk*tk≡1(mod mk),即ak*M/mk*tk≡ak(mod mk)
故∑ai*M/mi*ti≡ak(mod mk)
4.代码:
(其中LL是long long,qcm是快速乘)

1 LL crt(){ 2 LL bwl=0; 3 for(int i=1;i<=k;++i){ 4 LL x,y; 5 exgcd(M/m[i],m[i],x,y); 6 if(x<0) x=x%m[i]+m[i]; 7 bwl=(bwl+qcm(qcm(a[i],M/m[i]),x))%M; 8 } 9 return (bwl+M)%M; 10 }
5.孙子算经:
《孙子算经》:今有物不知其数,三三数之剩二;五五数之剩三;七七数之剩二。问物几何?
《算法统宗》:三人同行七十稀,五树梅花廿一枝,七子团圆月正半,除百零五便得知。
其中70=7*5*2,70%3=1,21=3*7*1,21%5=1,15(半个月)=3*5*1,15%7=1
用70*2+21*3+15*2=233除3*5*7=105,得到的余数23即为答案
70=3*5*2,21=3*7*1,15=3*5*1三式中的最后一个乘数2、1、1即为上文提到的di
数字还挺吉利的233
扩展中国剩余定理:
1.一次同余方程组:
扩展中国剩余定理的主要用途是解一次同余方程组,其中m1,m2,...,mn不一定互质
2.扩展中国剩余定理:
令前k-1个方程组成的同余方程组的一个解为x
且M为前k-1个模数的lcm
则前k-1个方程的方程组的通解为x+i*M
现在将第k个方程加入
只需求一个正整数t,使得
x+t*M≡ak(mod mk)
可以转化为M*t+mk*y=ak-x
然后用exgcd求出t
若此方程无解,则整个同余方程组无解
否则x+t*M为前k个方程的方程组的一个解
(这段也是我抄的,原文和上边一样orz)
3.代码:
(其中LL是long long,qcm是快速乘,三个参数分别为两个乘数和模数)

1 LL excrt(){ 2 LL M=m[1],ans=a[1]; 3 for(int i=2;i<=k;++i){ 4 LL x,y; 5 LL d=gcd(M,m[i]); 6 LL c=(a[i]-ans%m[i]+m[i])%m[i]; 7 if(c%d) return -1; 8 exgcd(M,m[i],x,y); 9 x=qcm(x,c/d,m[i]/d); 10 ans+=qcm(x,M,M*m[i]); 11 M*=m[i]/d; 12 ans=(ans%M+M)%M; 13 } 14 return ans; 15 }
4.细节:
1.有些题数字卡得严,必须要用快速乘
2.快速乘时注意第二个乘数必须为正,要用通解处理
3.每次快速乘的模数不一定一样,需要好好考虑
例题:
洛谷3868 猜数字
洛谷4777 扩展中国剩余定理




 浙公网安备 33010602011771号
浙公网安备 33010602011771号