【转载】自动机理论 (Automata Theory) 基础

简介

自动机理论是对抽象机 (abstract machines) 和自动机 (automata) 的研究，以及可以使用它们解决的计算问题。它是理论计算机科学中的一个理论。

自动机一词来自希腊语 αὐτόματος，意思是“自我行动、任性、自我行动”。自动机（复数自动机）是一种抽象的自行式计算设备，它自动遵循预定的操作顺序。状态数有限的自动机称为有限自动机 (FA) 或有限状态机 (FSM)。自动机系列可以用层次形式来解释，其中有限状态机是最简单的自动机，图灵机是最复杂的。

 

下图说明了有限状态机，这是一种众所周知的自动机类型。这个自动机包括状态（图中用圆圈表示）和转换（用箭头表示）。当自动机看到一个输入符号时，它会根据其转换函数转换（或跳转）到另一个状态，该函数将先前的状态和当前输入符号作为其参数。

 

自动机理论与形式语言理论密切相关。在这种情况下，自动机被用作可能是无限的形式语言的有限表示。自动机通常按它们可以识别的形式语言类别进行分类，如乔姆斯基层次结构，它描述了自动机主要类别之间的嵌套关系。自动机在计算理论、编译器构造、人工智能、语法分析和形式验证方面发挥着重要作用。

自动机 (Automata) 是机器的抽象模型，它通过移动一系列状态或配置来对输入 (inputs) 执行计算。在计算的每个状态，转换函数根据当前配置的有限部分确定下一个配置。因此，一旦计算达到可接受的配置，它就会接受该输入。最通用和最强大的自动机是图灵机。

形式定义

 

 

    

 

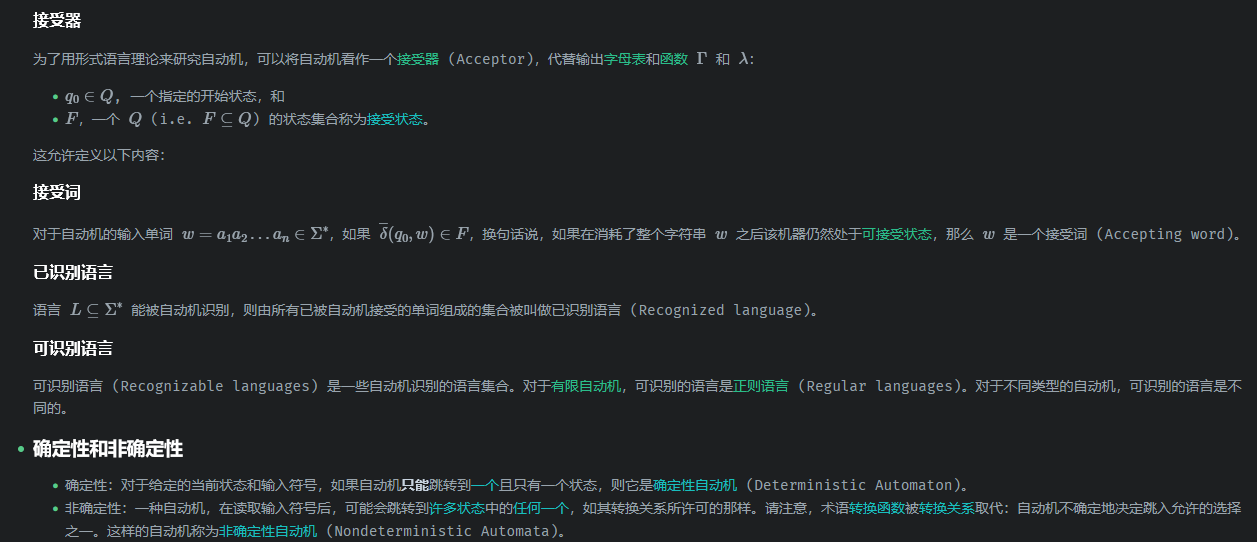
应用

自动机理论中的每个模型都在几个应用领域中发挥着重要作用。有限自动机用于文本处理、编译器和硬件设计。上下文无关文法(CFG) 用于编程语言和人工智能。

最初，CFG 用于人类语言的研究。元胞自动机被用于人工生命领域，最著名的例子是约翰康威的生命游戏。其他一些可以用生物学中的自动机理论解释的例子包括软体动物和松果的生长和色素沉着模式。更进一步，一些科学家提倡一种理论，认为整个宇宙是由某种离散自动机计算的。这个想法起源于 Konrad Zuse 的作品，并由 Edward Fredkin 在美国推广。

自动机也出现在有限域理论中：不可约多项式的集合，可以写成二次多项式的组合，实际上是一种正则语言。可以使用自动机解决的另一个问题是正则言的归纳。

自动机模拟器

自动机模拟器是用于教授、学习和研究自动机理论的教学工具。自动机模拟器将自动机的描述作为输入，然后模拟其对任意输入字符串的工作。可以通过多种方式输入自动机的描述。自动机可以用符号语言定义， 或者可以以预先设计的形式输入其规格，或者可以通过单击和拖动鼠标来绘制其转换图。众所周知的自动机模拟器包括 Turing’s World、JFLAP、VAS、TAGS 和 SimStudio。

参考资料：

> https://cs.stanford.edu/people/eroberts/courses/soco/projects/2004-05/automata-theory/basics.html

> https://en.wikipedia.org/wiki/Automata_theory

转载：https://www.lumin.tech/articles/automata-theory-basics/