【计算机组成原理】原码、补码、移码的作用---减法运算的原理\整数比较数的大小
由于计算机的减法器 ,造价高,所就用加法器来运行加法计算,原理如下:
减法运算的原理
为啥减法运算可以转化成加法运算,原理是什么?
以下举例:以mod=12(时钟)
x mod m=?
补充知识点
来源:数论
整数:包含负整数 、0、正整数
余数的定义
数论中余数的定义 :如果a和d是两个自然数,d非0,可以证明存在两个唯一的整数q和r,满足a = qd + r 且0 ≤ r < d。 其中,q被称为商(整数), r被称为余数。
-3 =(-1)*12+9
9 = 0*12+9
21 = 1*12+9
33 = 2*12+9
-15=(-2)*12+9
M mod运算 就是取余数运算,进位的部分被舍弃,将数字分成0~(M-1)类,每一类都是余数等价的,所以-3,9 21。。。余数都是等价的,计算的时候可以用替换。例如-3mod 12=9 mod 12
(mod 12)把所有整数分为12类 余数为o~11
mod 12余数相同的数,都是同一类,都是等价的
即10+(-3)、10+9、10+21... mod 12 的条件下效果相同
补数
以下举例:以mod=12(时钟)
|A|+|B|=12 那么称为A B互为补数
9=12-|-3|
mod=|负数|+补数,所以补数一定为正数,因此一个减法运算可以转化为补数的加法运算
字长与mod的关系
计算的字长是固定的,计算机加法结果超过字长的部分会舍弃,留下部分就是余数。所以计算机是天然的取模运算,mod=2字长。
2字长=|负数|+补数
因此一个减法运算可以转化为补数的加法运算例如:
(|负数|+A) mod 2字长=(补数+A)mod 2字长。二进制的补数=补码,
字长为8的计算机 的加法运算,就是mod为28的加法运算,加完的结果就是余数,进位的部分自然被舍弃,因为超出的部分计算机无法表示。
补码的作用 ----减法运算
补码=负数的补数
使用处码可将减法操作转变光等价的加法,ALU中无需集成减法器,执行加法操作时,符号位一起参与运算。
移码的作用-----整数比较数的大小
移码:补码的基础上将符号位取反。注意:移码只能用于表示整数
移码会随着真值的递增,看那个数的左边bit位先为1,就谁大。 所以就可以使用计算机硬件实现整数的大小对比。
移码:不管正负数,只要将其补码的符号位取反即可。
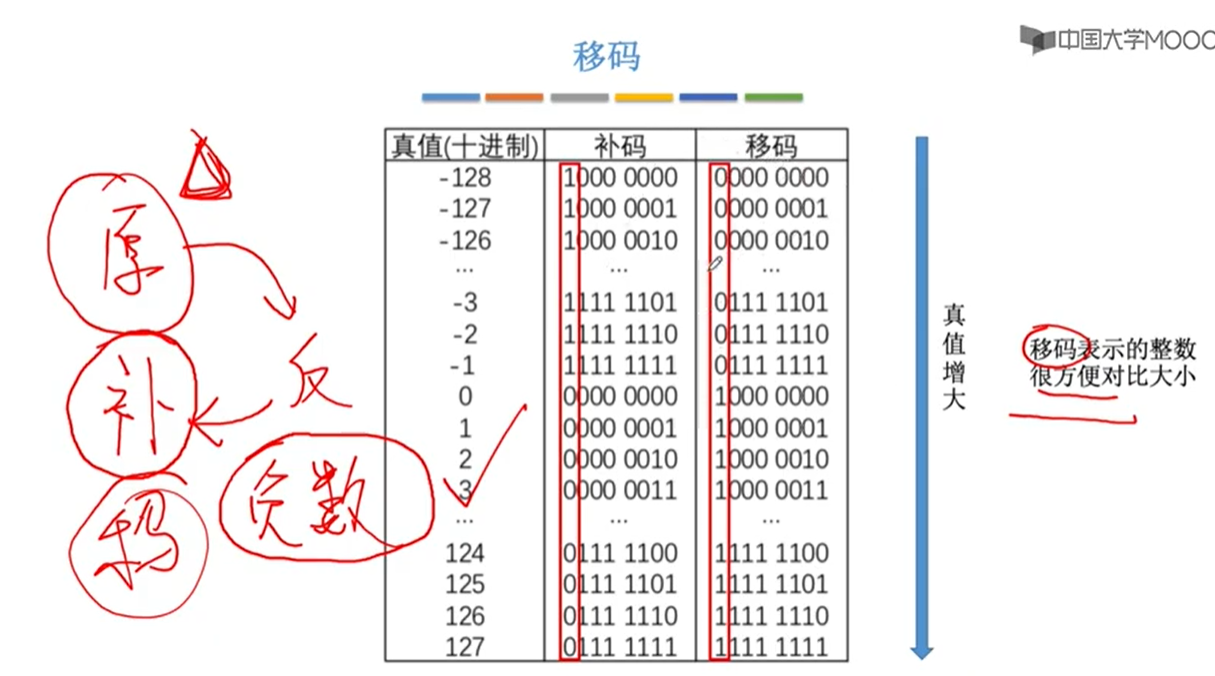
结论
二进制的减法可以转化成加法运算。利用mod=|负数|+补数 ,计算机的mod =2字长 ,计算的字长是固定的,计算机加法结果超过字长的部分会舍弃,留下部分就是余数。
练习
为什么计算的补数=反码+1?
加1后才能进位,表示mod 长。
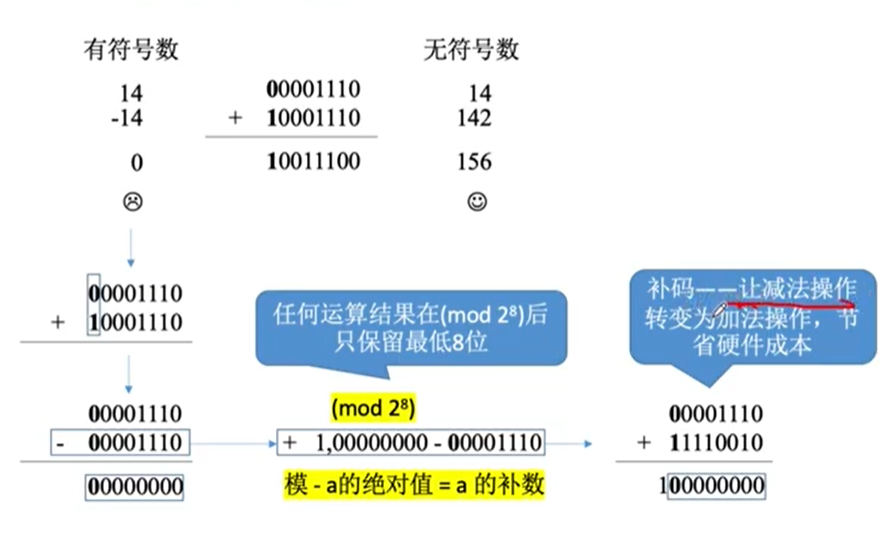
计算溢出




 浙公网安备 33010602011771号
浙公网安备 33010602011771号