【计算机组成原理】定点数的表示

 

 

 

 

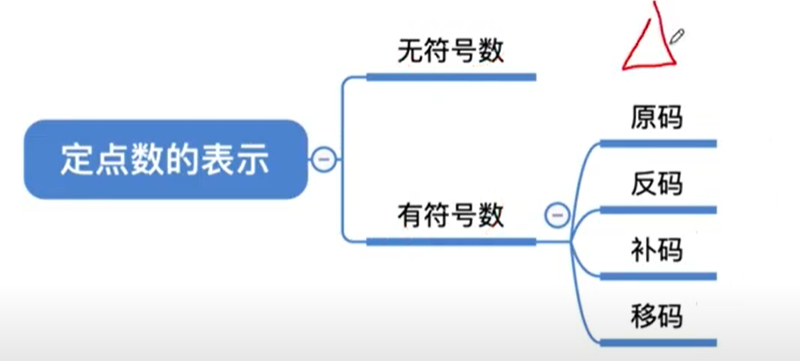
定点表示

机器数中的小数点位置是固定不变的，小数点不再使用“.”表示，而是约定它的位置。小数点：隐含存储（定点数：事先约定；浮点数：按规则浮动）

这里有两种简单的约定，将小数点的位置固定在数据的最高位之前，或固定在最低位之后。一般称前者为定点小数后者为定点整数。

定点小数

+0.75 = 0.11B 存储为011

-0.75 = 1.11B 存储为111

TIPS：小数点后面两位 绝对值0.00 ～0.11 = 1-0.01（不明白）

 

n位的 无符号整数的表示范围的两种思路

（1）递推 然后求和，结果是等比数列求和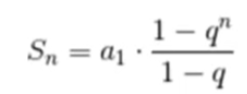

 

 

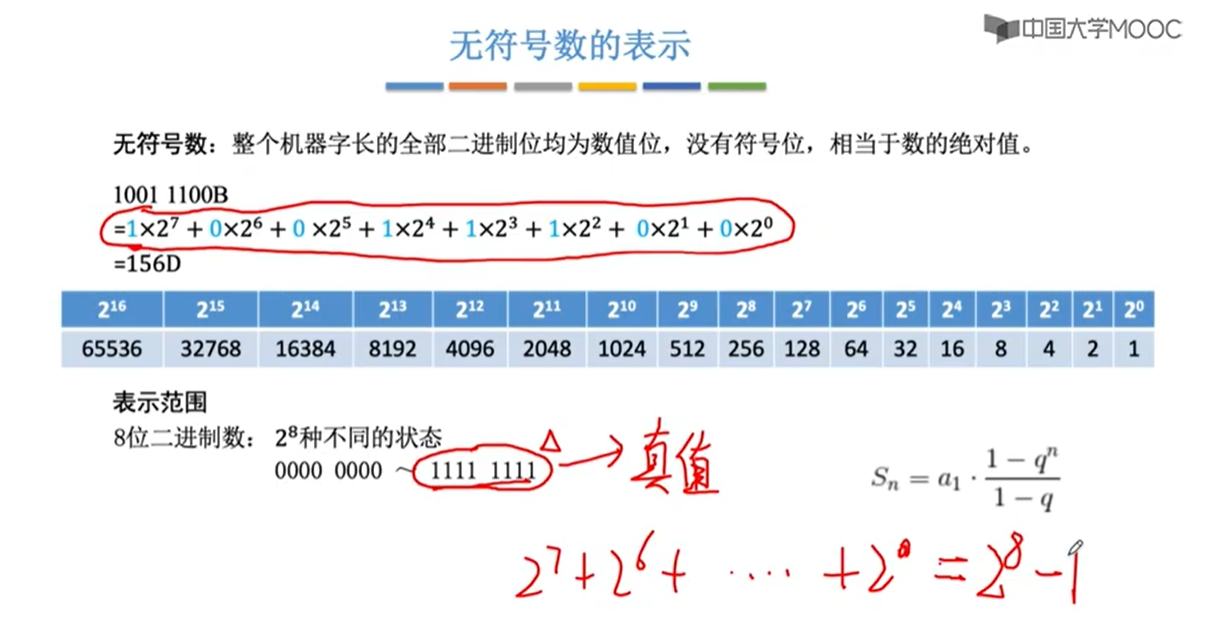
备注：真值 是带符号的数字如：+1 、-1

 （2）逻辑推导，8位二进制，最高大数是1111 1111 +1=1  0000 0000 =2^8-1。

 

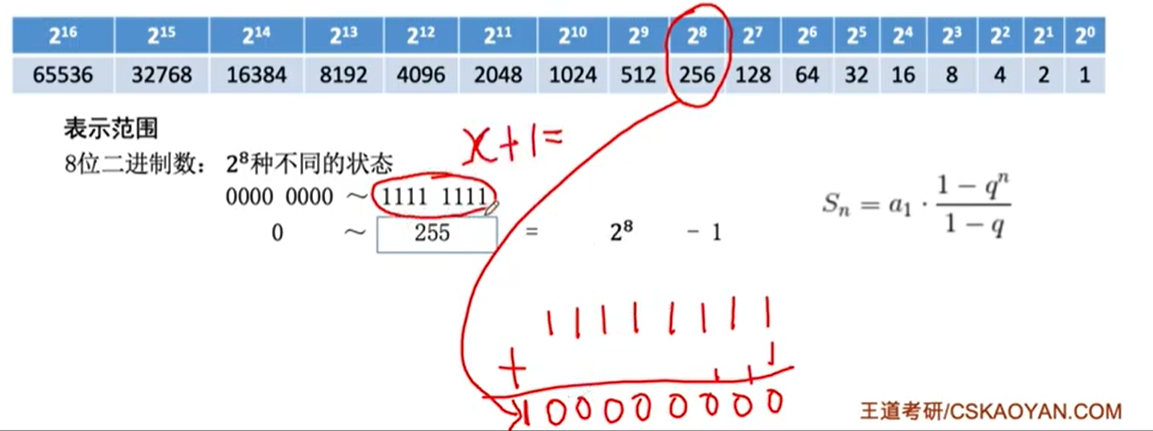
因此n位无符号整数的表示范围：0~2ⁿ-1

有符号数的顶点表示法

 

 

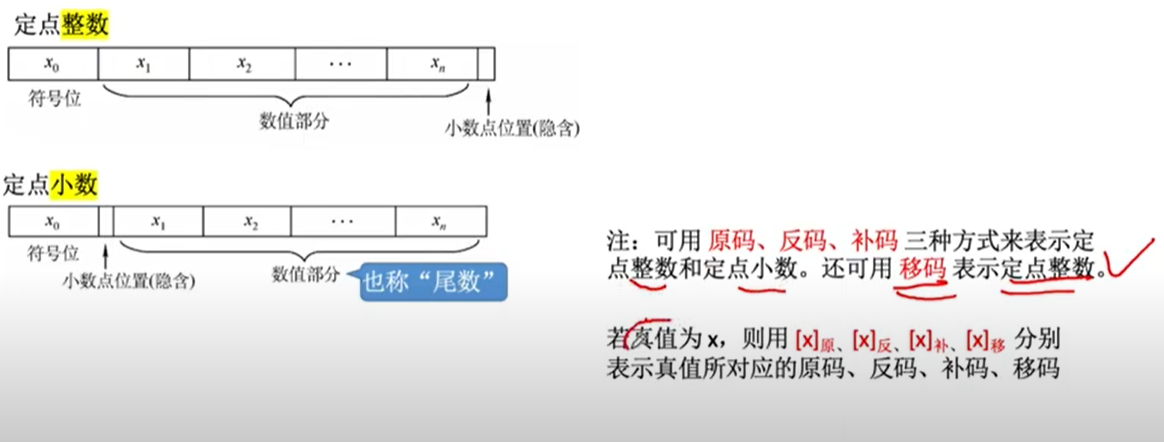
 将一个浮点数用定点表示保存 例如19.75

必须将整数的19和小数的0.75分开保存

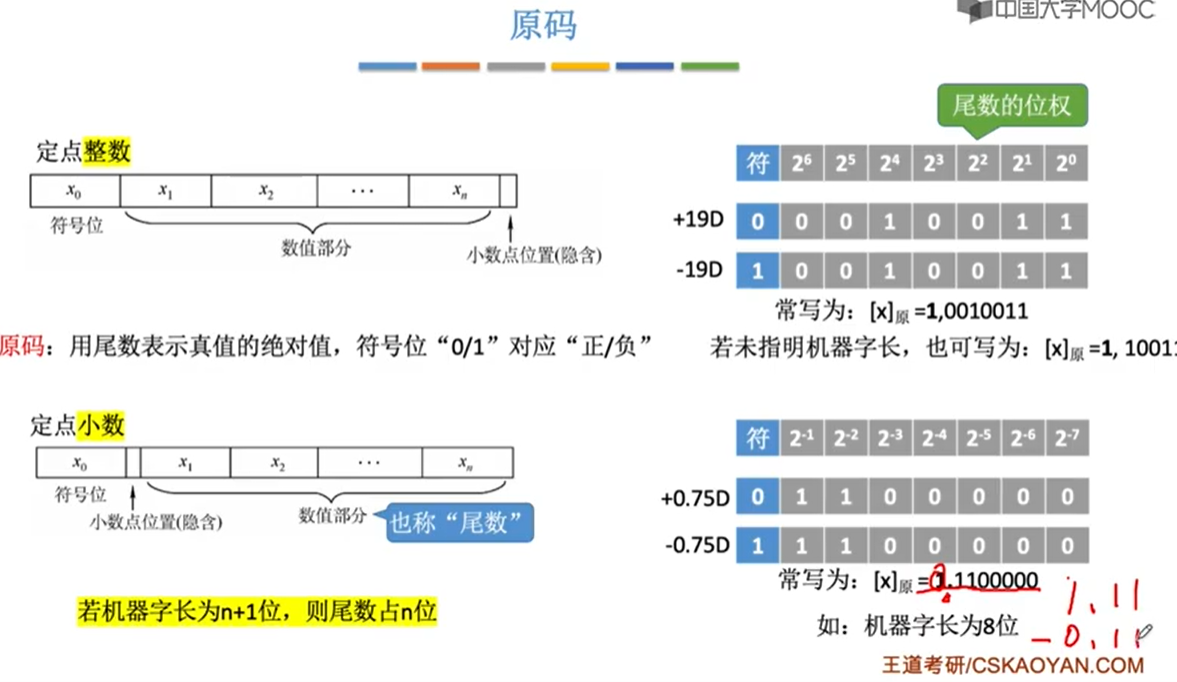
原码和反码取值范围

定点整数的取值范围

 

 

 若机器字长n+1位，原码整数的表示范围:-(2ⁿ-1)≤x≤2ⁿ-1(关于原点对称)
真值表示范围：-(2ⁿ⁺¹-1)≤x≤2ⁿ⁺¹-1 

 

定点小数数的取值范围

 

 若机器字长n+1位，原码小数的表示范围:-(1-2^-n)≤x≤1-2^-n（等比求和公式 计算得出）。

原码小数的取值范围：符号位为0的时候最大1-2^-n，符号位为1的时候最小-(1-2^-n)

 

 

 

补码取值范围（考点）

 

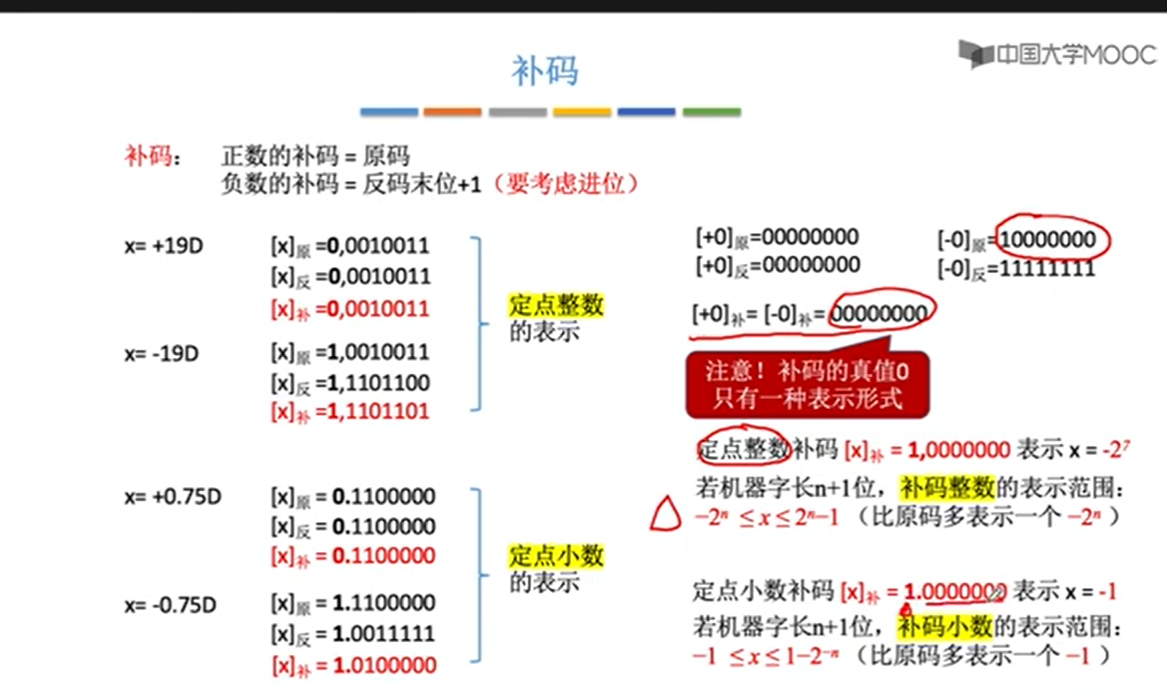
定点整数补码[x]_补= 1,0000000表示x=-2^字长-1。定点小数补码[x]_补=1.00000表示x=-1

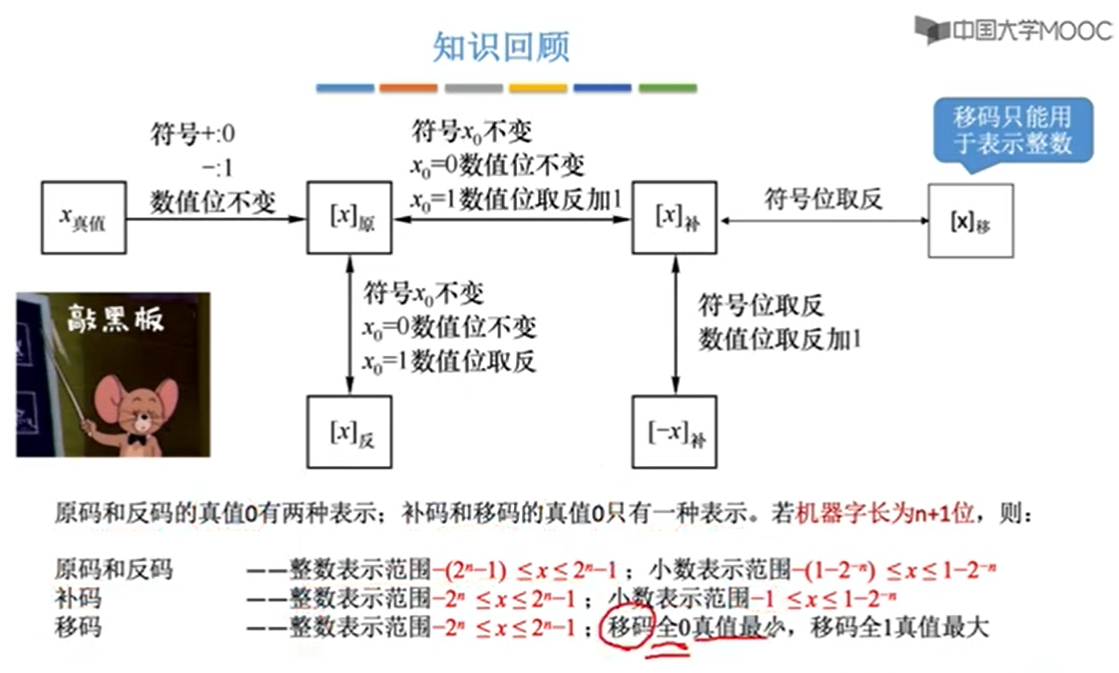
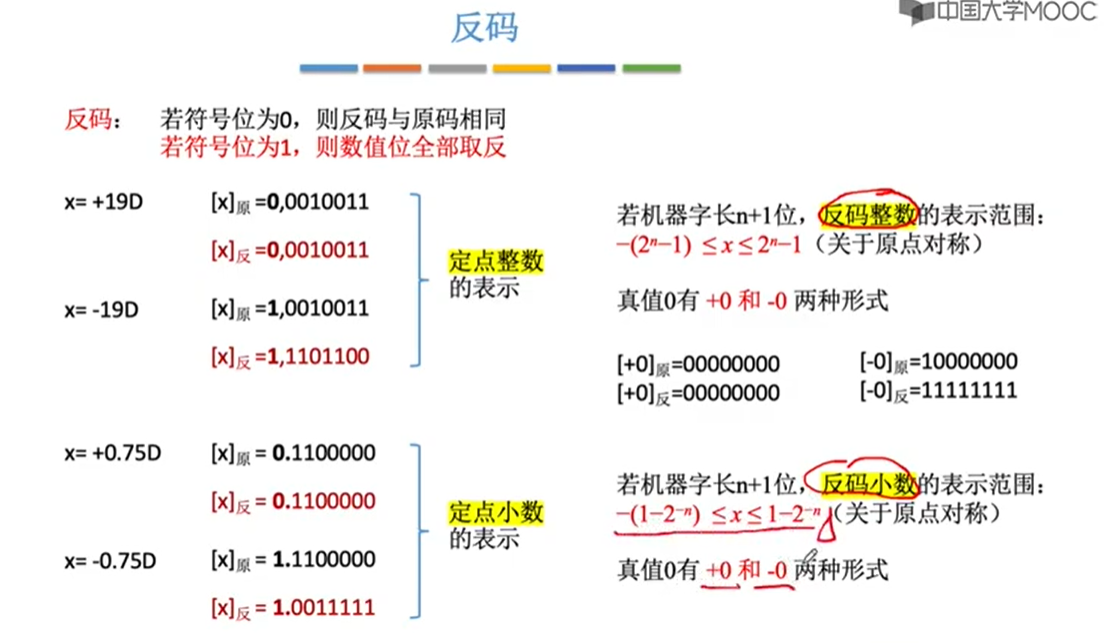
原码和补码的转化

整数补码是它本身

负整数和负小数的补码都是符号位不变，其他位置取反 再加1，补码转原码过程一样。

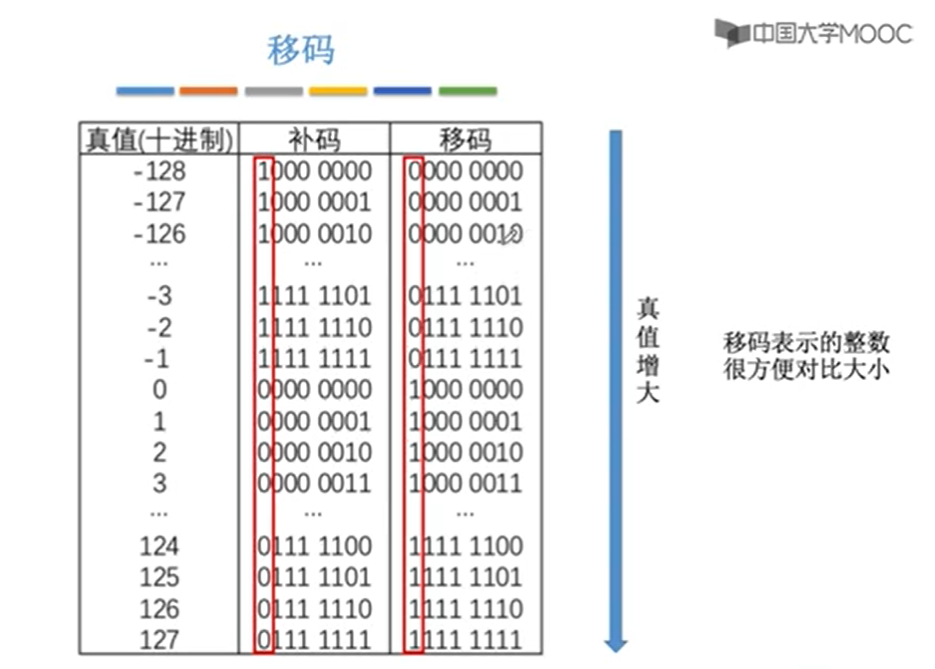
移码

移码：补码的基础上将符号位取反。注意:移码只能用于表示整数

移动和补码是一一对应的，所以取值范围是一样的

作用：用于判断大小，谁先出现1谁就大

 

移码作用

用于判断大小，谁先出现1谁就大

 

 

 

 

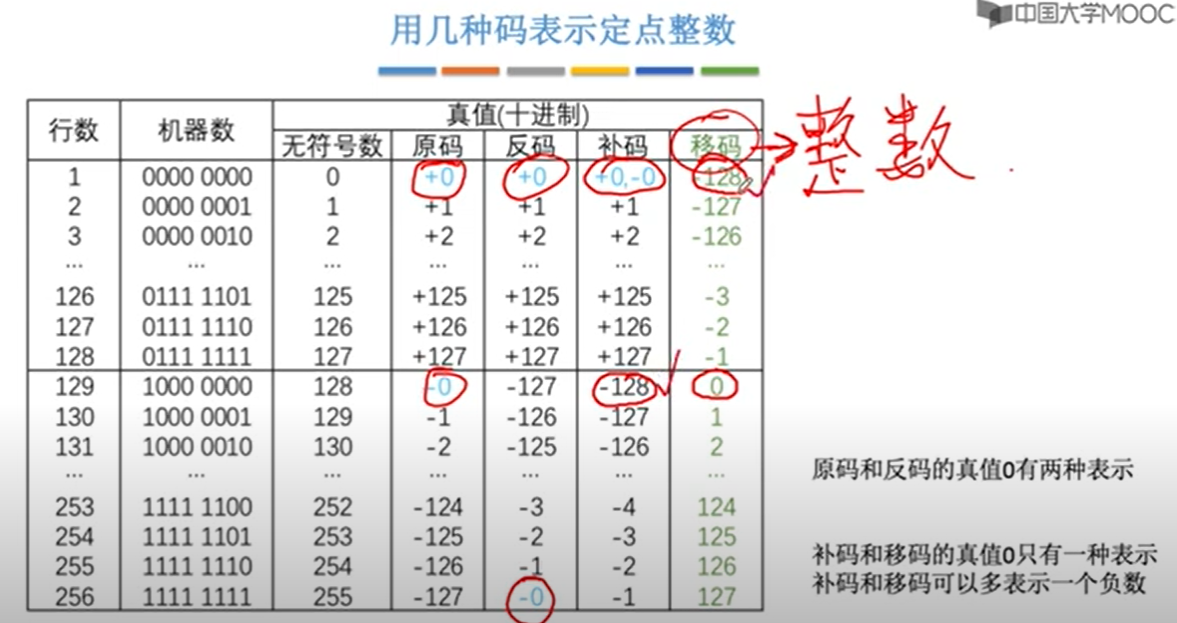
 定点数中的比例因子

计算机采用定点数表示时，对于既有整数又有小数的原始数据，需要设定一个比例因子，数据按比例因子缩小成定点小数或扩大成定点整数再参加运算，结果输出时再按比例折算成实际值。

比例因子必须选择恰当。选择不当，将会影响运算精度，或者会使运算结果超出机器所能表示的数据范围，即出现溢出。

【例题】在定点小数机器中计算 11.01＋10.01 选择比例因子2^{-2}＝0.01，可将两操作数变换为 0.1101＋0.1001 但 0.1101＋0.1001＝1.0110，运算结果不是纯小数，出现了机器数不能表示的数，即出现了正溢出。 如果选择比例因子 2^{-3}＝0.001，可将两操作数变换为 0.01101＋0.01001 则运算结果 0.01101＋0.01001＝0.10110 为正常结果。将0.10110除以比例因子2^{-3}，可得到正确结果 101.10

 练习

练习题1

 

 

 练习题2

 

2种[x]_补转向[-x]_补方法

（1）[x]_补符号位、数值位全部取反，末位+1

（2）[x]_补=>[x]_原=>[-x]_{补:2次和正常的求补。}

 练习题3