【C# 排序】堆排序 heap sort

概览

 

 

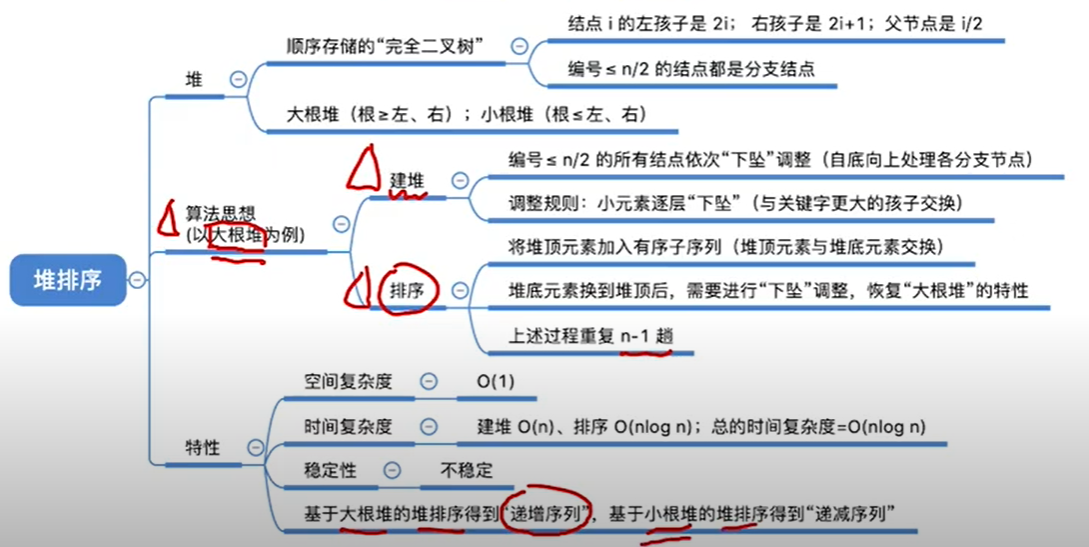
定义

堆排序（英语：Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子节点的键值或索引总是小于（或者大于）它的父节点。

 

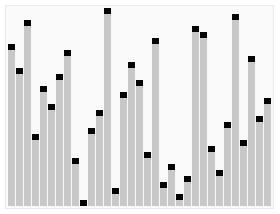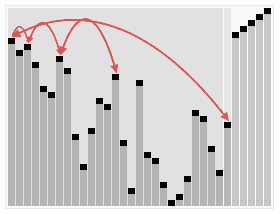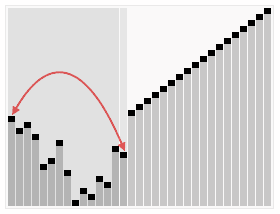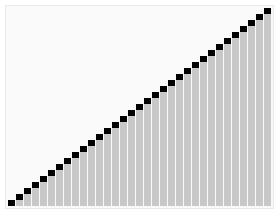
完全二叉树的知识

数组索引是从0开始

通常堆是通过一维数组来实现的。在阵列起始位置为0的情形中：
父节点i的左子节点在位置  (2i+1)
父节点i的右子节点在位置  (2i+2)
子节点i的父节点在位置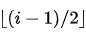

 树高：log₂ⁿ

数组索引是从1开始

父节点i的左子节点在位置  (2i)
父节点i的右子节点在位置  (2i+1)
子节点i的父节点在位置n/2 向下取整

_2ⁿ⁺¹

执行步骤

（1）建立完全二叉树（大根堆或小根堆）

（2）排序

原地堆排序

基于以上堆相关的操作，我们可以很容易的定义堆排序。例如，假设我们已经读入一系列数据并创建了一个堆，一个最直观的算法就是反复的调用del_max()函数，因为该函数总是能够返回堆中最大的值，然后把它从堆中删除，从而对这一系列返回值的输出就得到了该序列的降序排列。真正的原地堆排序使用了另外一个小技巧。堆排序的过程是：

1. 建立一个堆 H [ 0.. n − 1 ] {\displaystyle H[0..n-1]}
2. 把堆首（最大值）和堆尾互换
3. 把堆的尺寸缩小1，并调用shift_down(0),目的是把新的数组顶端数据调整到相应位置
4. 重复步骤2，直到堆的尺寸为1

缺点

这里就牵涉到数据结构的理论里经常忽略的常数了。堆排序的常数太大了，而且是所有 O(n log n) 级的基本排序中，常数最大的一个。对于快排、归并、堆排，大家的用时虽然都是 O(n log n) 级的，但是堆排序所花的时间能达到快排的 1.6 ~ 2 倍。所以堆排序并不能取代快排的地位，只能作为快排划分退化后的保障手段，使得总体的情况“不至于太差”

（提一嘴，堆排常数大是因为它和其他排序相比，空间访问连续性很差，它在访问堆中的父子节点的时候是跳着访问的，极易造成访存失效）

稳定性

不稳定

使用 场景

长数组

C#代码

        public static void HeapSelectSort(int[] aa)
        {
            int it;
            int len=aa.Length-1;
            //构建完全二叉树,大想堆 根>=左右
            for (int i = (aa.Length-1) / 2; i >=0; i--)
            {
                HeapAdust(aa,i,aa.Length);
              
            }
            //将根节点和最后一个元素互换
            for (int spilt = len; spilt >0; spilt--)
            {
               it= aa[spilt] ;
                 aa[spilt] = aa[0];
                aa[0] = it;
                HeapAdust(aa,0,spilt-1);
            }


        }
        /// <summary>
        /// 堆排序法核心代码
        /// </summary>
        /// <param name="aa"></param>
        /// <param name="starti"></param>
        /// <param name="len"></param>
        private static void HeapAdust(int[] aa, int starti, int len)
        {
          
            int LI = (starti * 2 + 1);  //左孩子索引
            if (LI > len) return;//左孩子不存在,因为是完全二叉树,所以最孩子不存在,那么右孩子也不存在
            int root = aa[starti];
            // LI = LI * 2+1左孩子的左孩子,一次类推
            for ( ; LI < len-1; LI = LI * 2+1)
            {
                //右孩子是否比左孩子大  ,LI < len-1 判断,所以右孩子肯定存在 &&是短路运算符
                if (LI < len-1&&aa[LI] < aa[LI + 1])
                {
                    LI = LI + 1;// LI+1为右孩子
                }
                if (root > aa[LI]) break;
                else { 
                    //修改根节点的位置
                    aa[starti] = aa[LI];
                    starti = LI;
                }
            } 
            aa[starti] = root;
        }