【C# 数据结构与算法】红黑树
视频地址：2022考研计算机王道数据结构考点冲刺00 红黑树的定义和性质【新考点】 - YouTube
需要的知识储备
1、2-3-4树中翻转的概念
2、平衡二叉树中旋转的概念，请点击阅读平衡二叉树
3、二叉搜索树的概念，请点击阅读二叉搜索树
辅助理解的工具网站：Red/Black Tree
红黑树诞生背景
为什么要发明红黑树？
平衡二叉树AVL:插入/删除很容易破坏“平衡”特性，需要频繁调整树的形态。如:(插入操作导致不平衡，则需要先计算平衡因子，找到最小不平衡子树(时间开销大)，再进行LL/RR/LR/RL调整
红黑树RBT:插入/删除很多时候不会破坏“红黑”特性，无需频繁调整树的形态。即便需要调整，一般都可以在常数级时间内完成，红黑树是二叉排序树，为了改进平衡二叉树的性能设计的。
平衡官叉树:适用于以查为主、很少插入/删除的场景红黑树:适用于频繁插入、删除的场景，实用性更强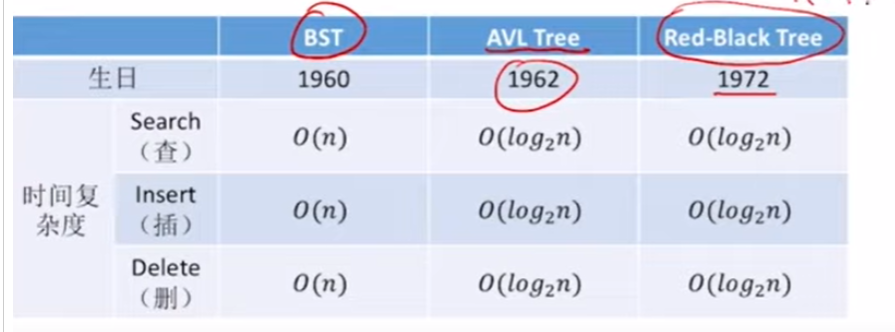
定义
它在1972年由鲁道夫·贝尔发明，被称为"对称二叉B树"，它现代的名字源于Leo J. Guibas和罗伯特·塞奇威克于1978年写的一篇论文。红黑树的结构复杂，但它的操作有着良好的最坏情况运行时间，并且在实践中高效：它可以在时间内完成查找、插入和删除，
是树中元素的数目。 红黑树是平衡二叉树，根据性质二，可以得出红黑树是平衡树。根据红黑树规则4可以得出用红色标注，是为了保存平衡，触发平衡机制。
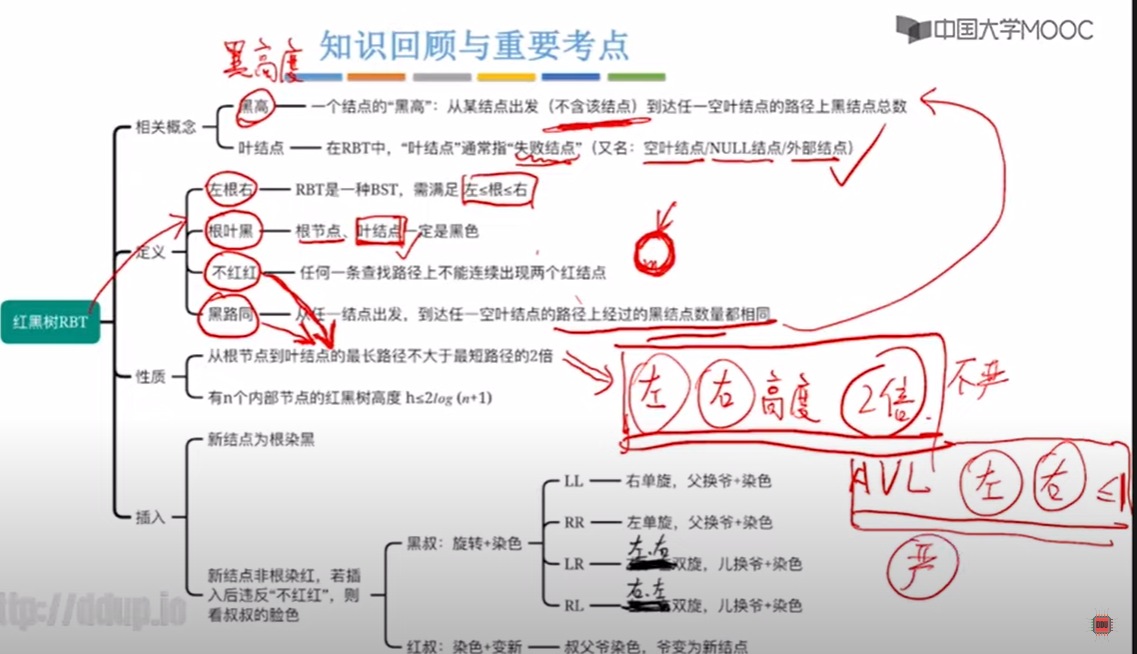
红黑树的规则
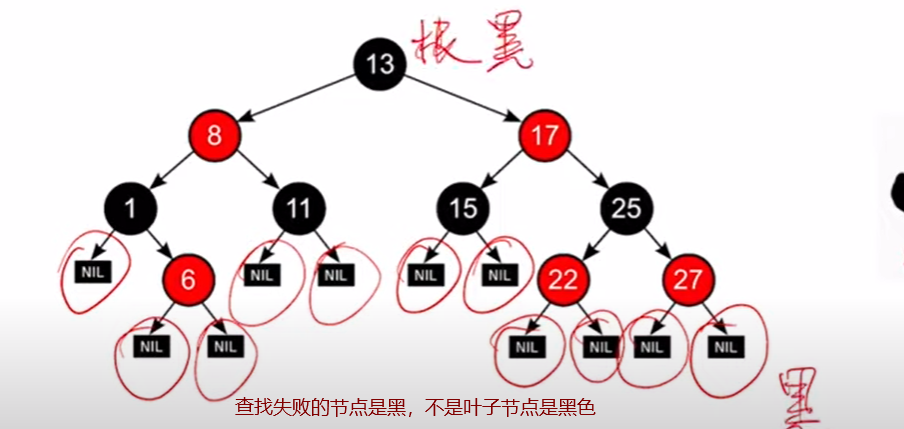
注意：nil是空节点，就是空指针。
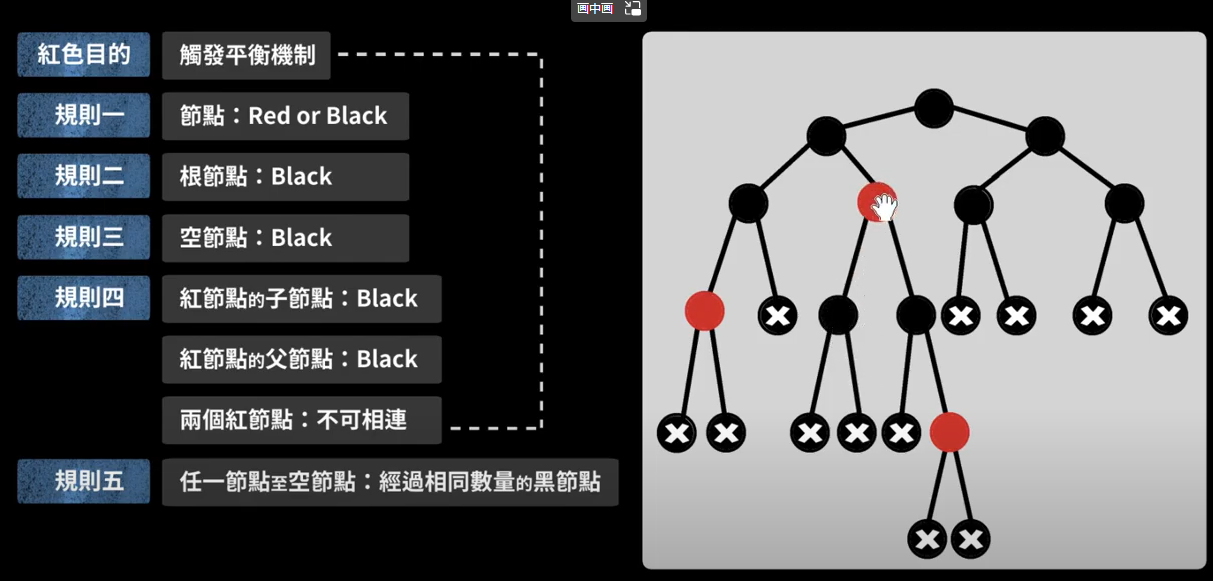
①每个结点或是红色，或是黑色的
②根节点是黑色的
③叶结点（外部结点|NULL结点|失败结点）均是黑色的√
④不存在两个相邻的红结点（即红结点的父节点和孩子结点均是黑色)
⑤任意一个节点到其叶子节点的所有路劲都包含相同数目的黑色节点
最后的叶子节点是为空的节点（null视为黑）。
简记：左根右，根叶黑，不红红，黑路同
红黑树的性质
性质1:根据规则得出 从根节点到叶结点的最长路径不大于最短路径的2倍性质。因此红黑树也是平衡树
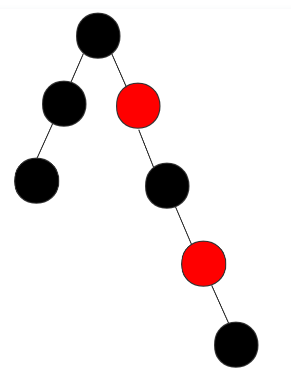
性质2:有n个内部节点的红黑树高度h ≤ 2logz(n＋1)
结构定义
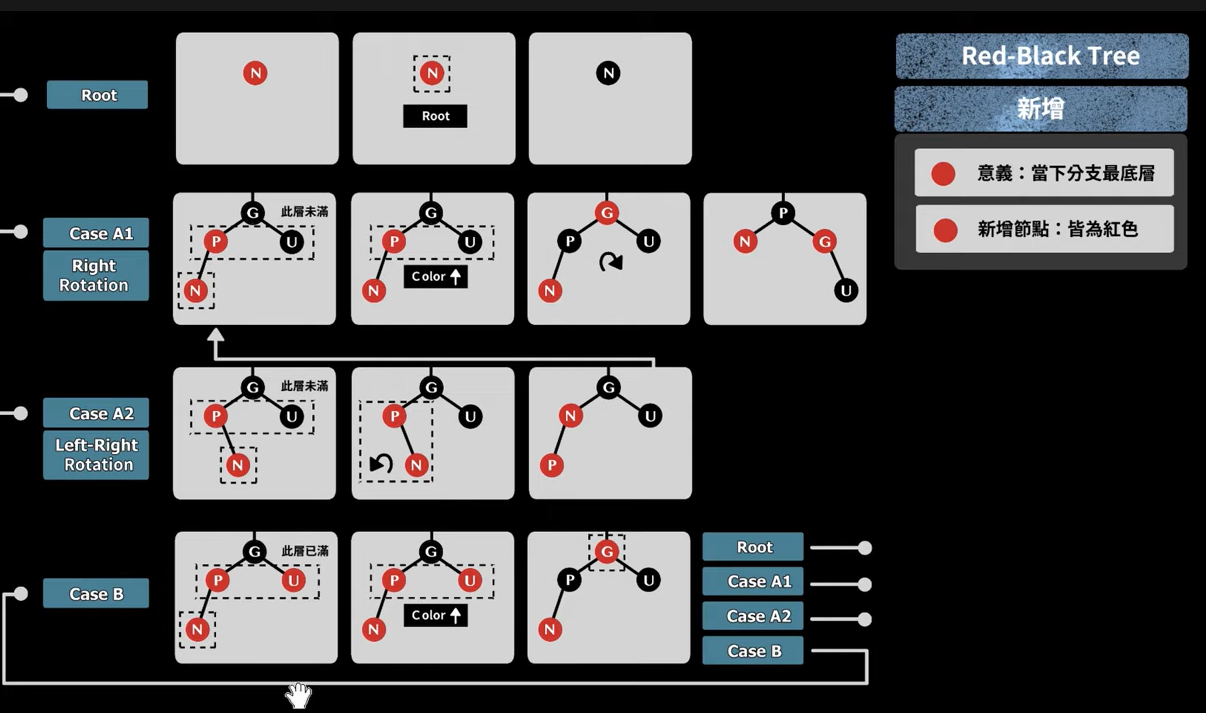
红黑树结点插入操作
为什么插入非根节点的位置要染为红色，因为为了符合“黑路同"这特性。
红黑树的插入，只会违法“不红红”的特性，因为左右根，根叶同，黑路同是不变的。
染色是：黑变红，红变黑。父换爷染色指父和爷都染色。儿换爷染色指儿爷都染色。总结出辈分发生变化的节点都要染色（除了根节点）。
知识点总结
