【C# 数据结构】平衡二叉树
平衡二叉树
AVL树可视化工具
AVL树可视化工具(旧金山大学 (usfca)|数据结构可视化工具)
自定义泛型平衡二叉树源码:https://files.cnblogs.com/files/blogs/700042/avlTreeT.rar?t=1654089460
一、平衡二叉树定义
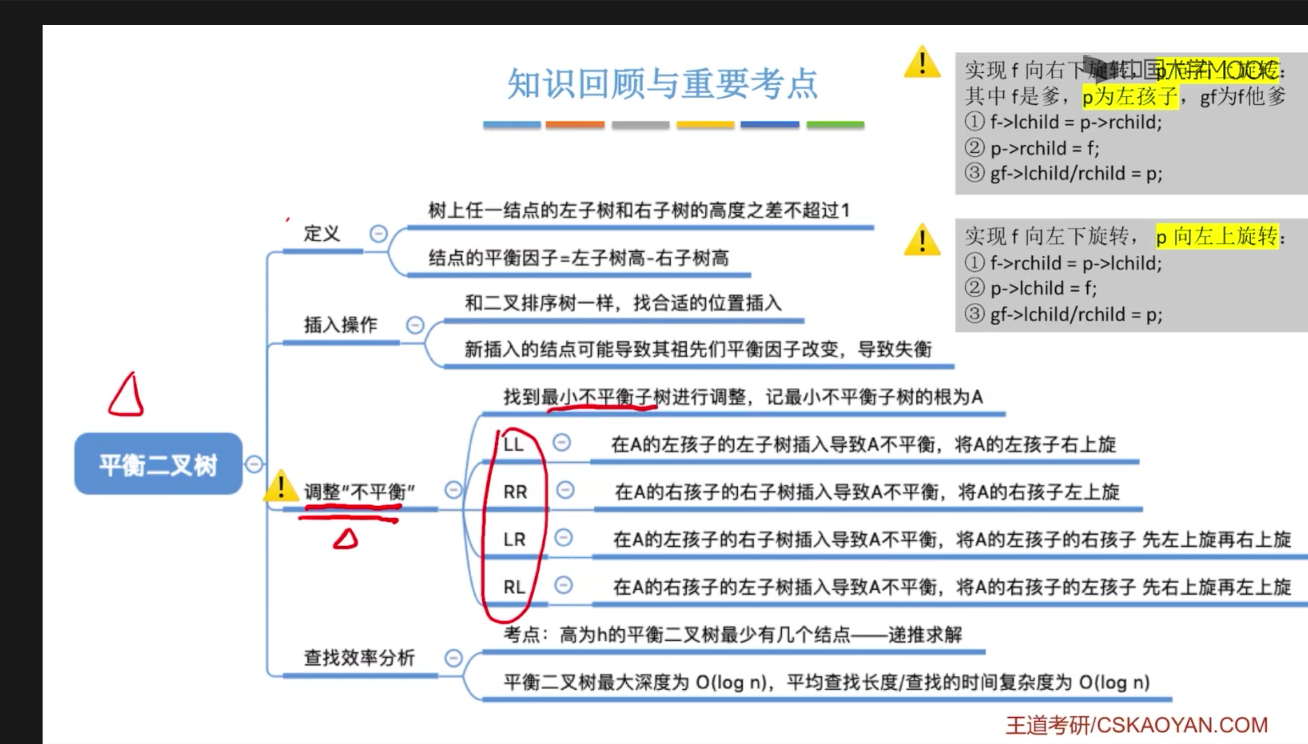
平衡二叉树又称AVL树。它可以是一颗空树,或者具有以下性质的二叉排序树:它的左子树和右子树的高度之差(平衡因子)的绝对值不超过1且它的左子树和右子树都是一颗平衡二叉树。
从上面简单的定义我们可以得出几个重要的信息:
- 平衡二叉树又称AVL树
- 平衡二叉树必须是二叉排序树
- 每个节点的平衡因子=左子树和右子树的高度差至多为1。
二、平衡因子(balance factor)
节点的平衡因子是它的左子树的高度减去它的右子树的高度(有时相反)。带有平衡因子1、0或 -1的节点被认为是平衡的。带有平衡因子 -2或2的节点被认为是不平衡的,并需要重新平衡这个树。平衡因子可以直接存储在每个节点中,或从可能存储在节点中的子树高度计算出来。
BalanceFactor=左子树高度-右子树高度
三、操作
删除
删除节点导致失衡,AVL需要维护从被删除节点到根节点root这条路径上所有节点的平衡,旋转的量级为O(logN)
插入
最多旋转2次
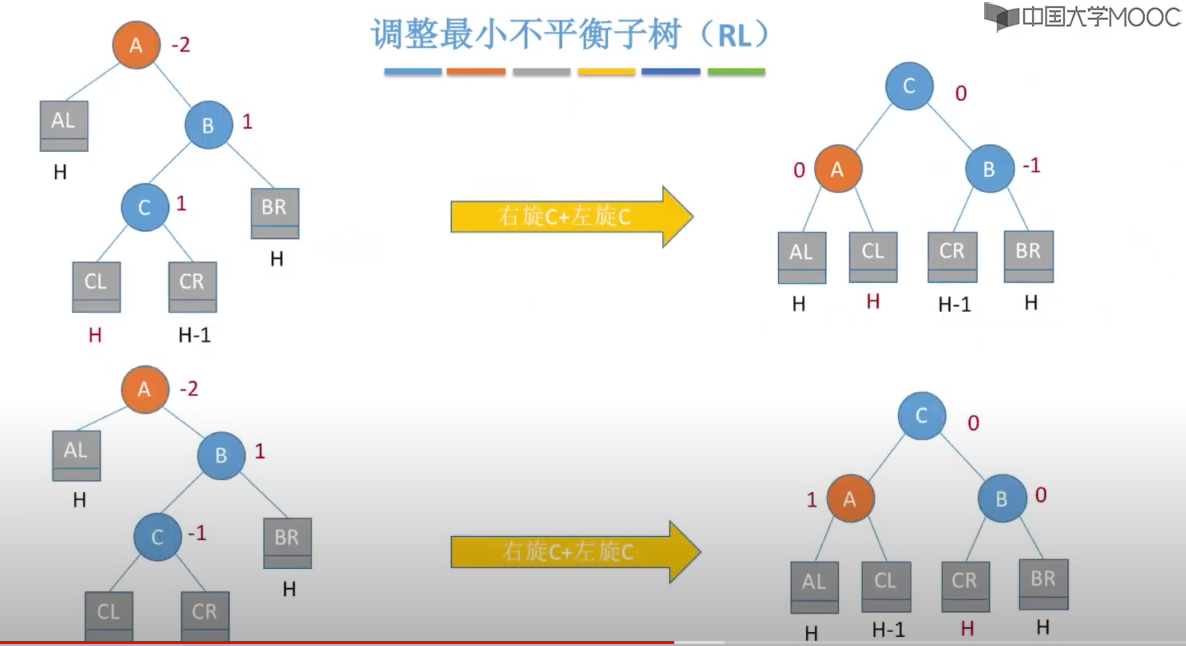
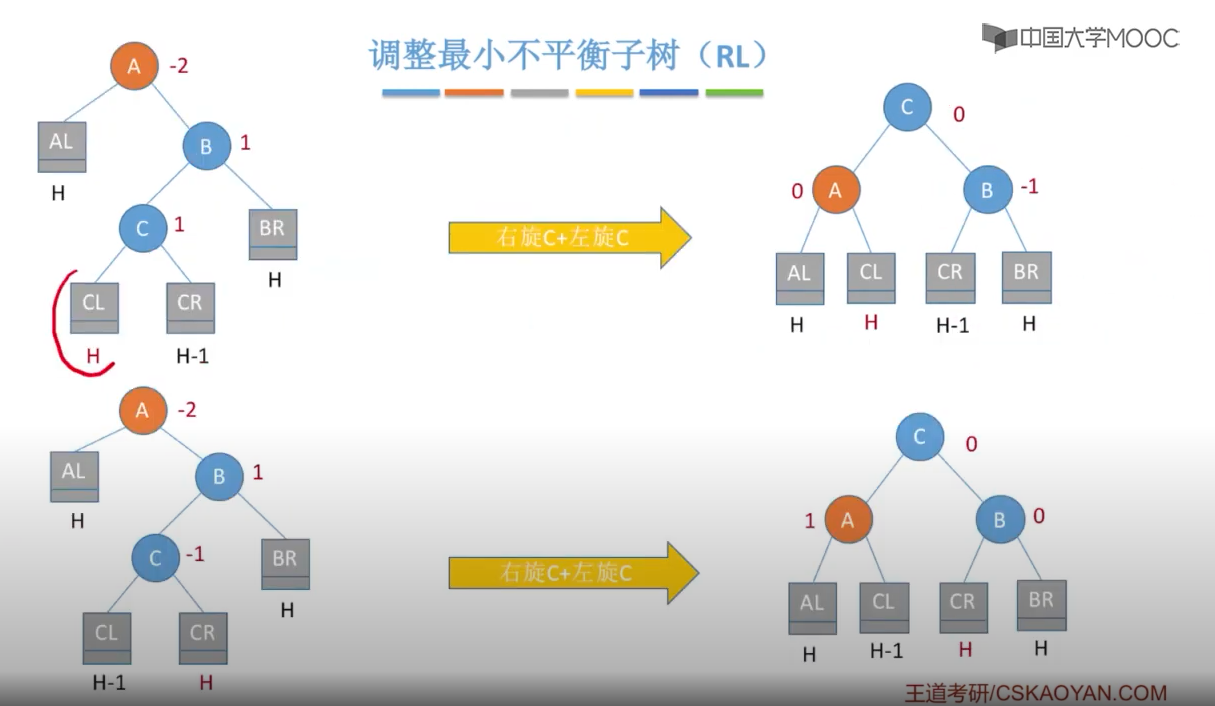
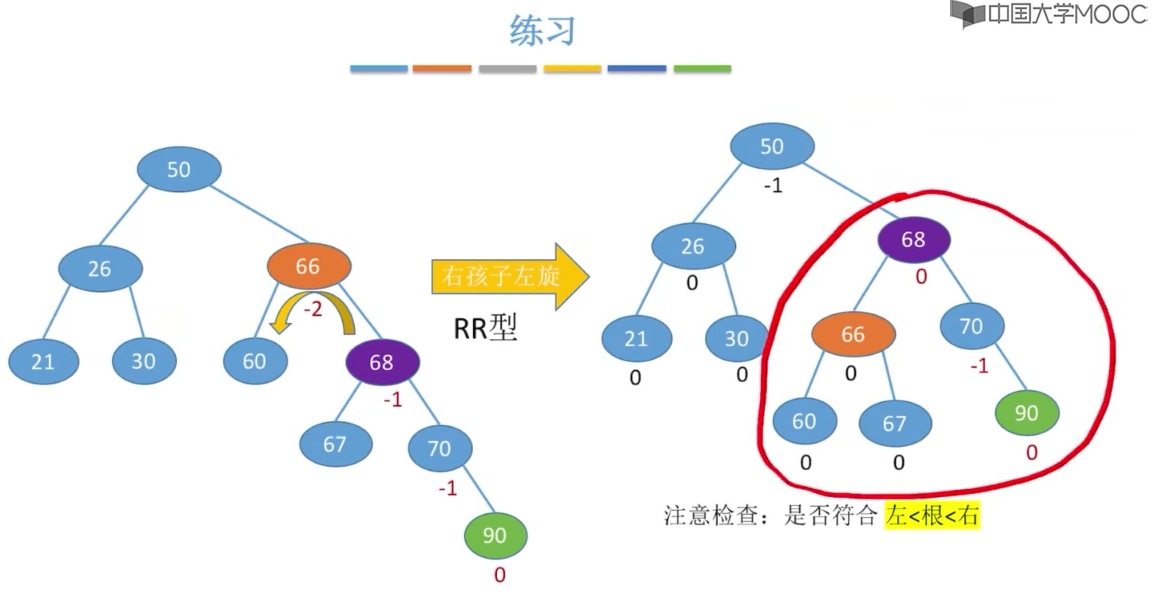
当插入新节点导致不平衡时,就调整最小的不平衡子树
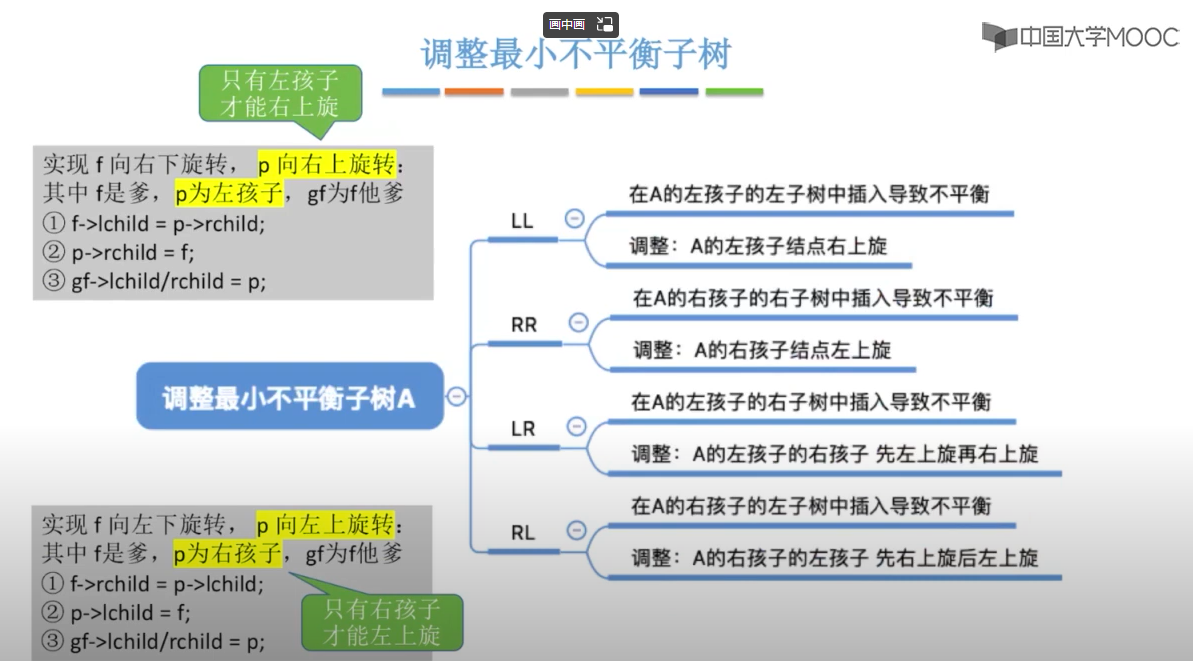
AVL树的基本操作一般涉及运作同在不平衡的二叉查找树所运作的同样的算法。但是要进行预先或随后做一次或多次所谓的"AVL旋转"。
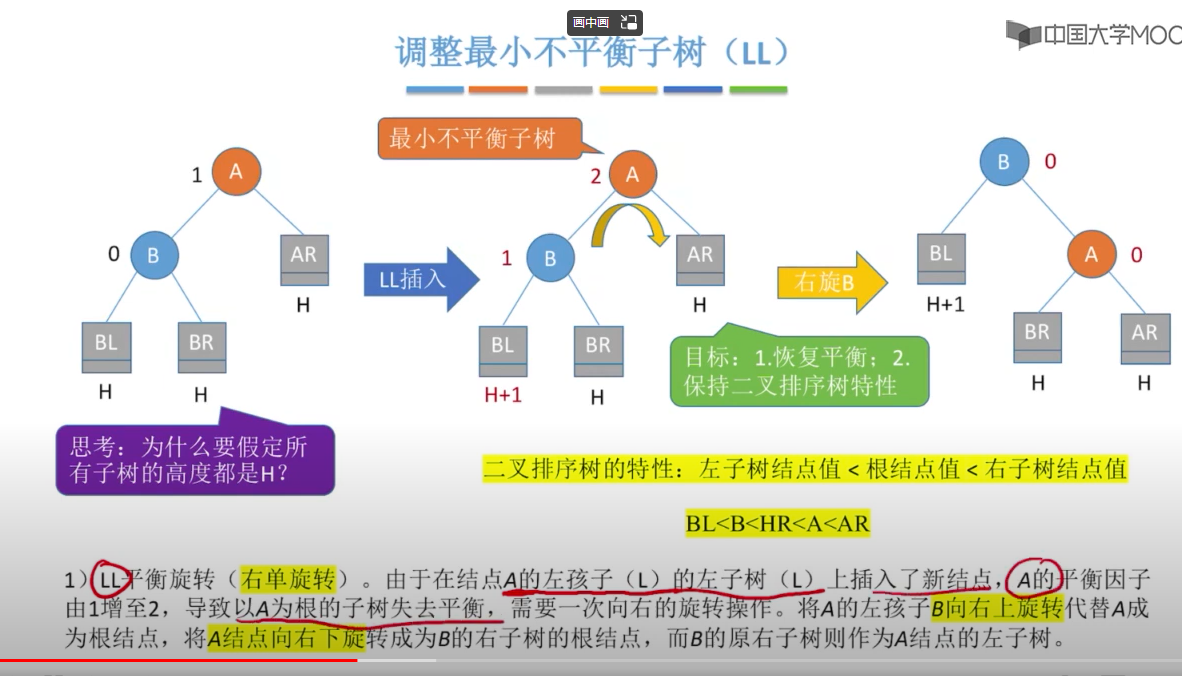
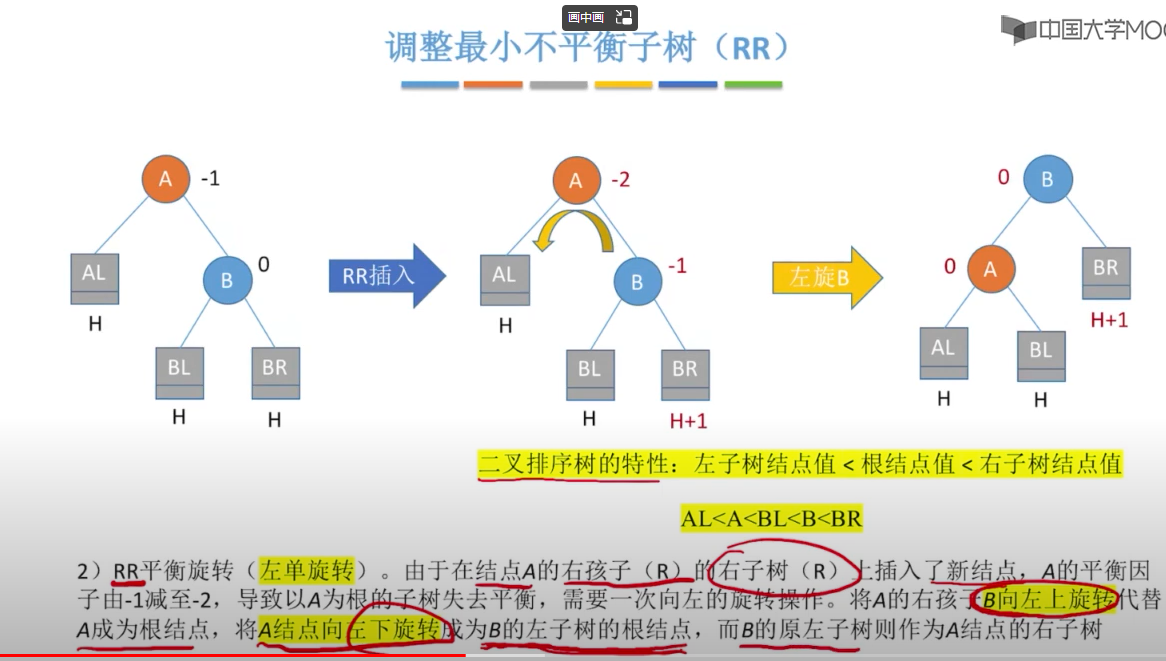
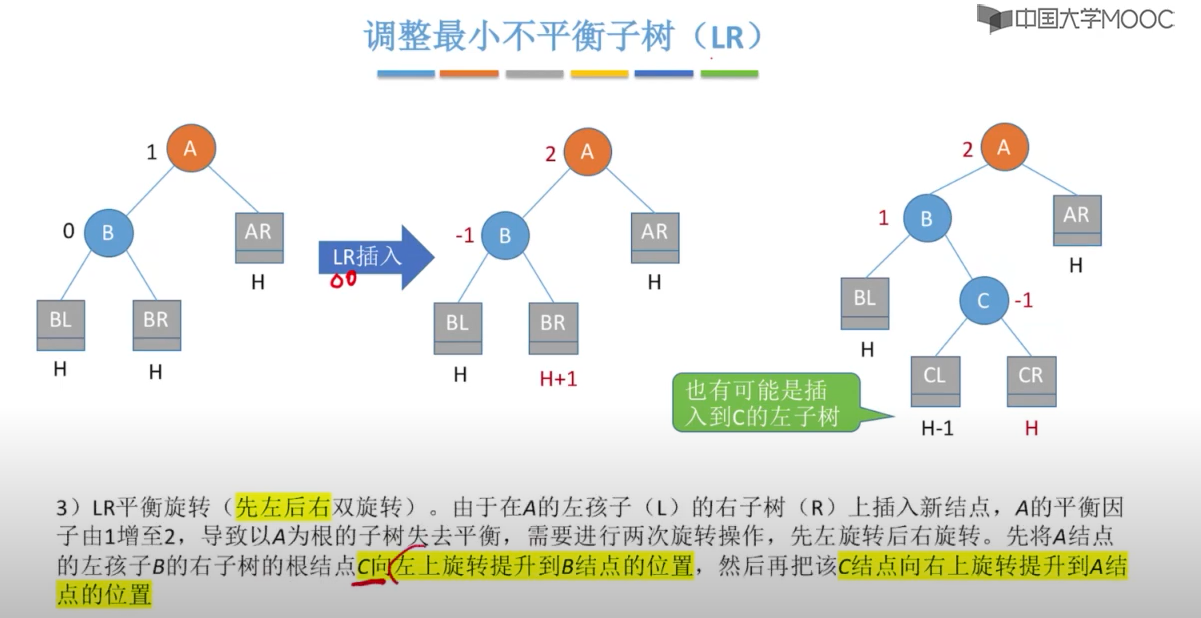
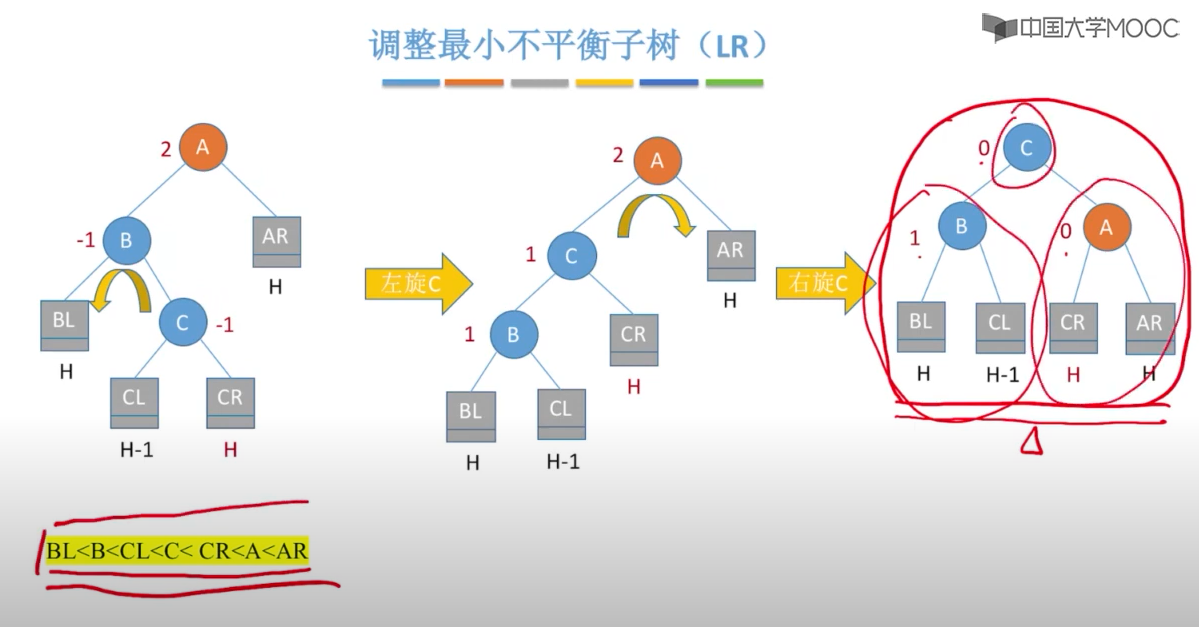
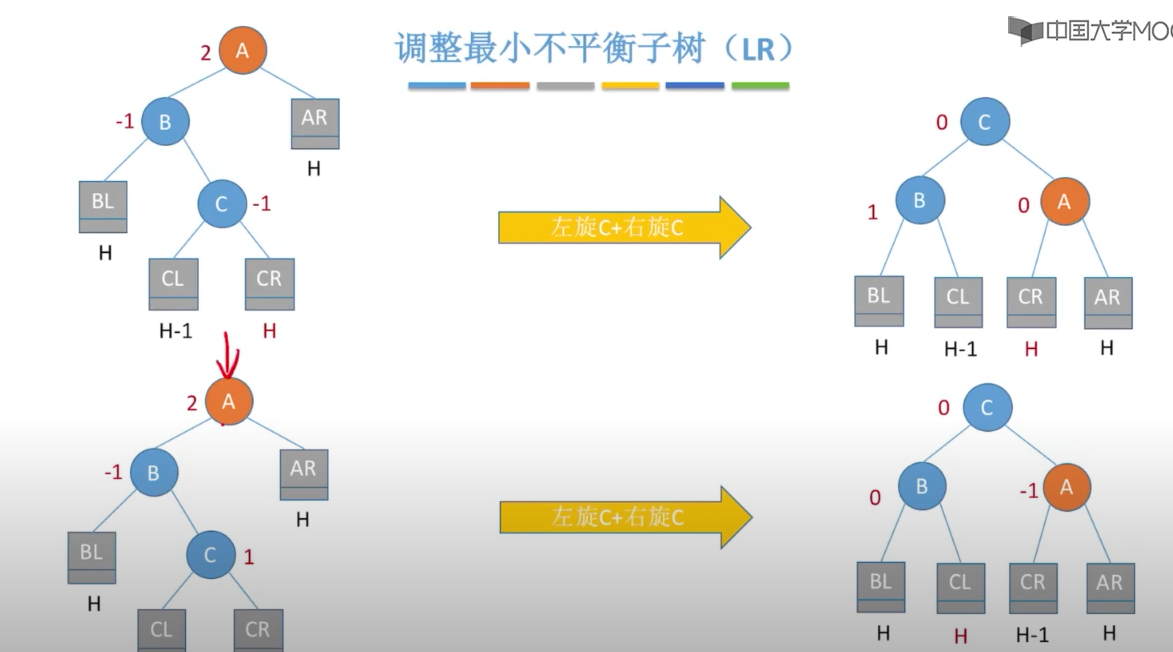
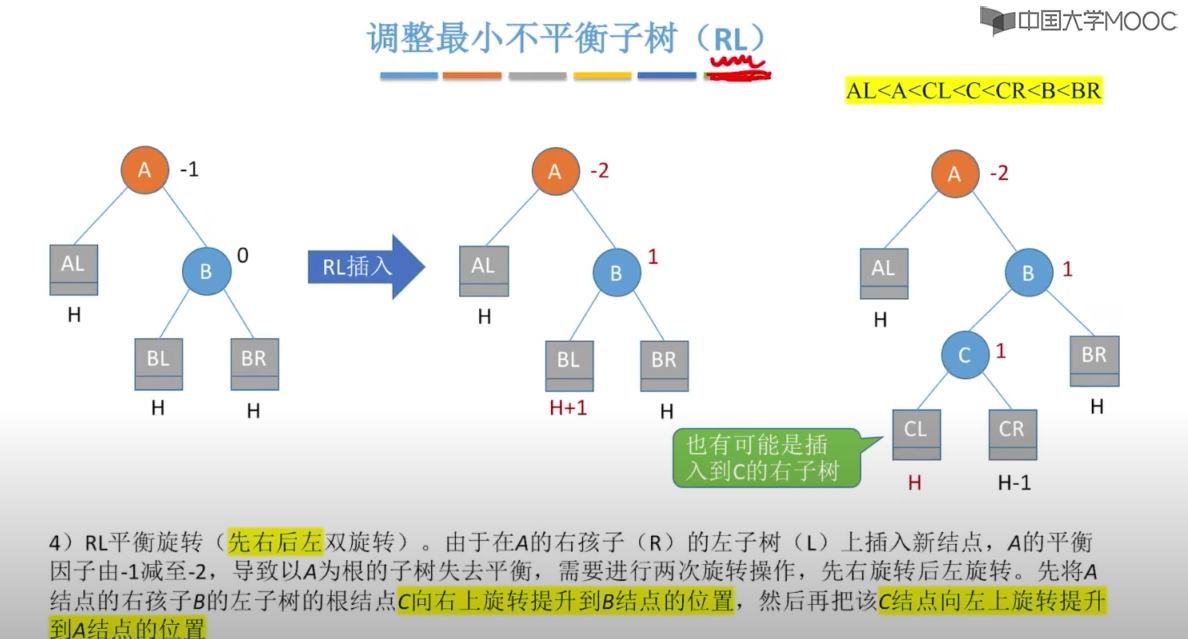
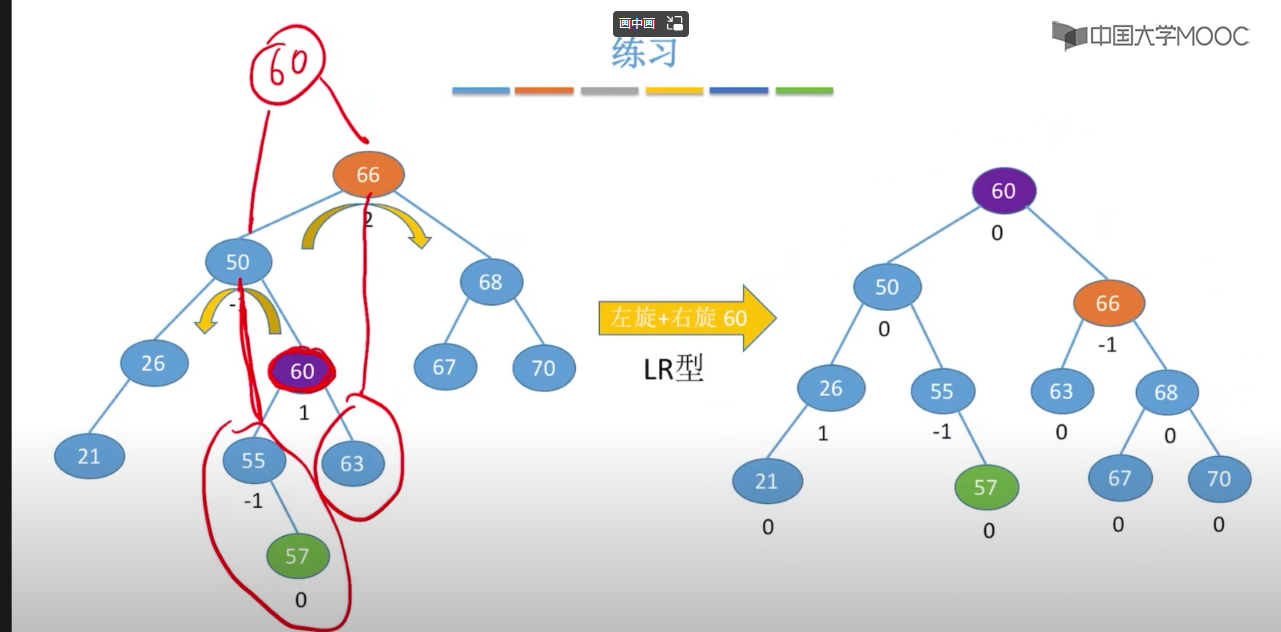
以下图表以四列表示四种情况,每行表示在该种情况下要进行的操作。在左左(LL)和右右(RR)的情况下,只需要进行一次旋转操作;在左右(LR)和右左(RL)的情况下,需要进行两次旋转操作。


在插入操作中,只要将最小不平衡子树调整A平衡,则其他祖先结点都会恢复平衡
选择规则如下:

四、最小的不平衡子树
当插入新节点导致不平衡时,就调整最小的不平衡子树
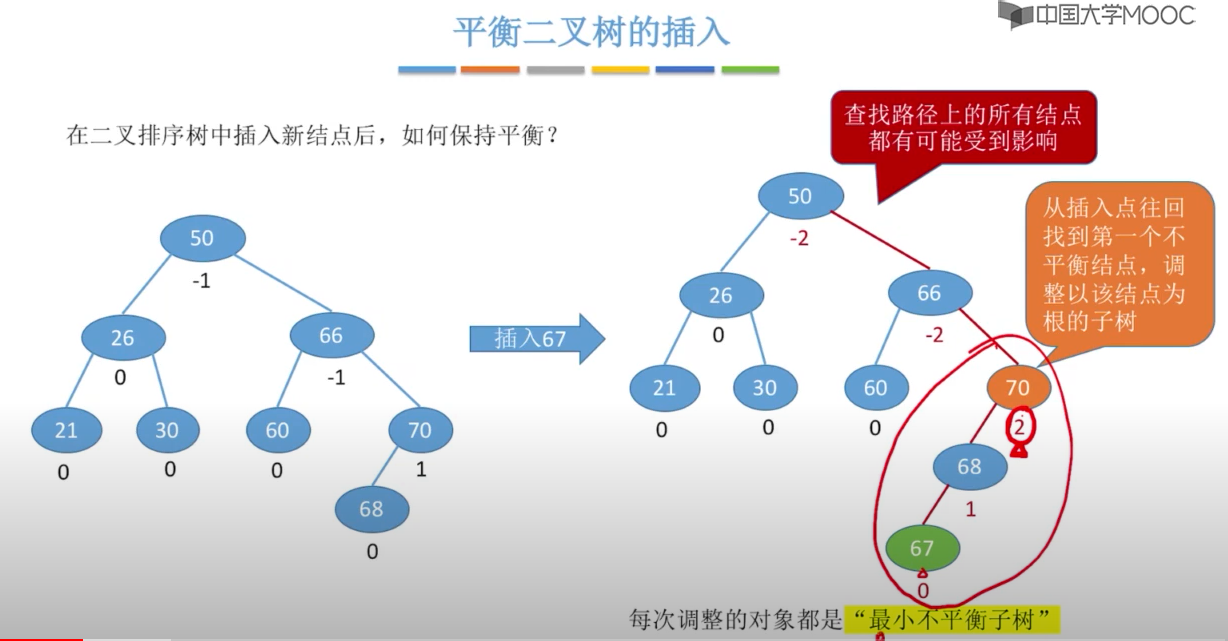
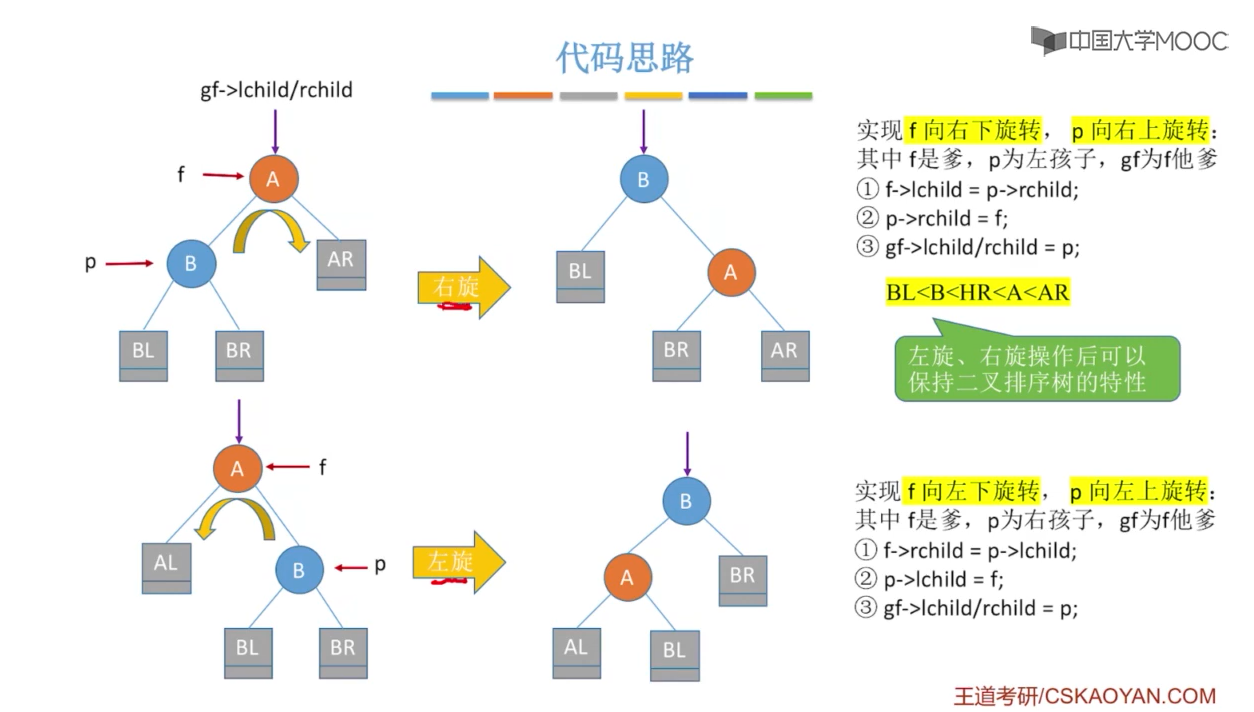
调整规则:

平衡二叉树的查找复杂度


证明如下:所有可以推出平衡二叉树的最大深度。
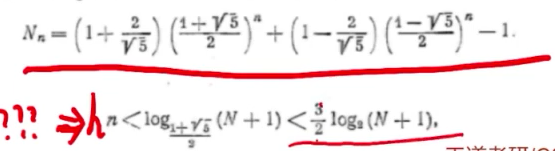
编程是个人爱好


 浙公网安备 33010602011771号
浙公网安备 33010602011771号