【C# 数据结构】二叉排序树
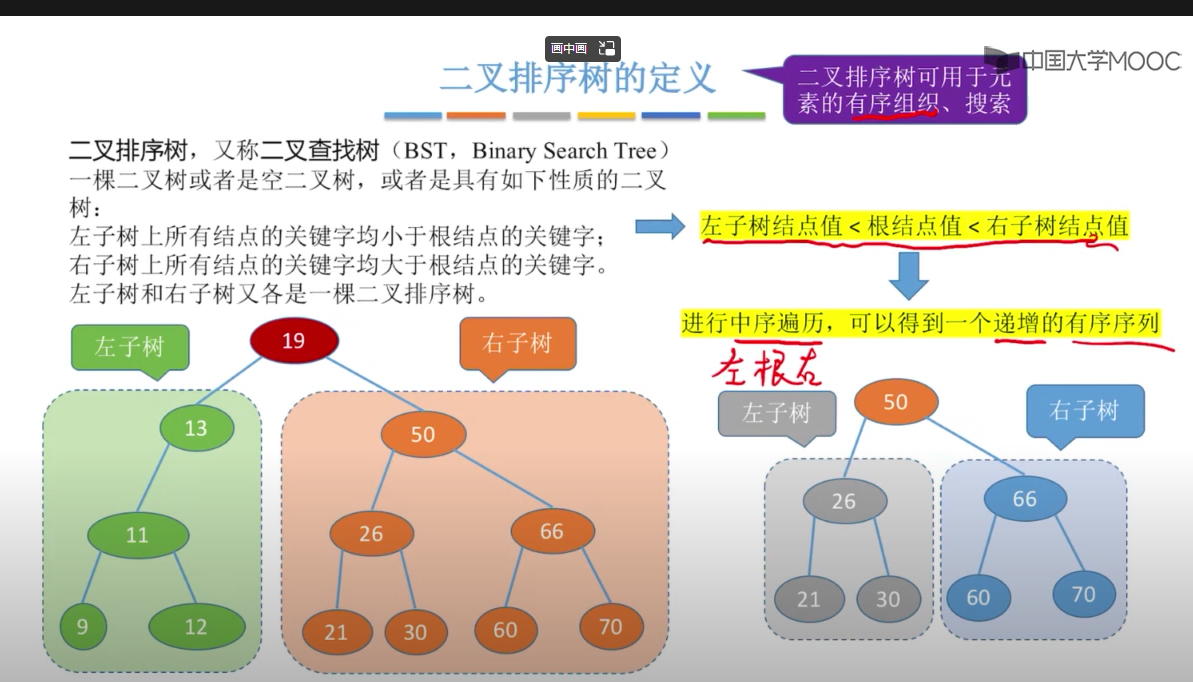
定义
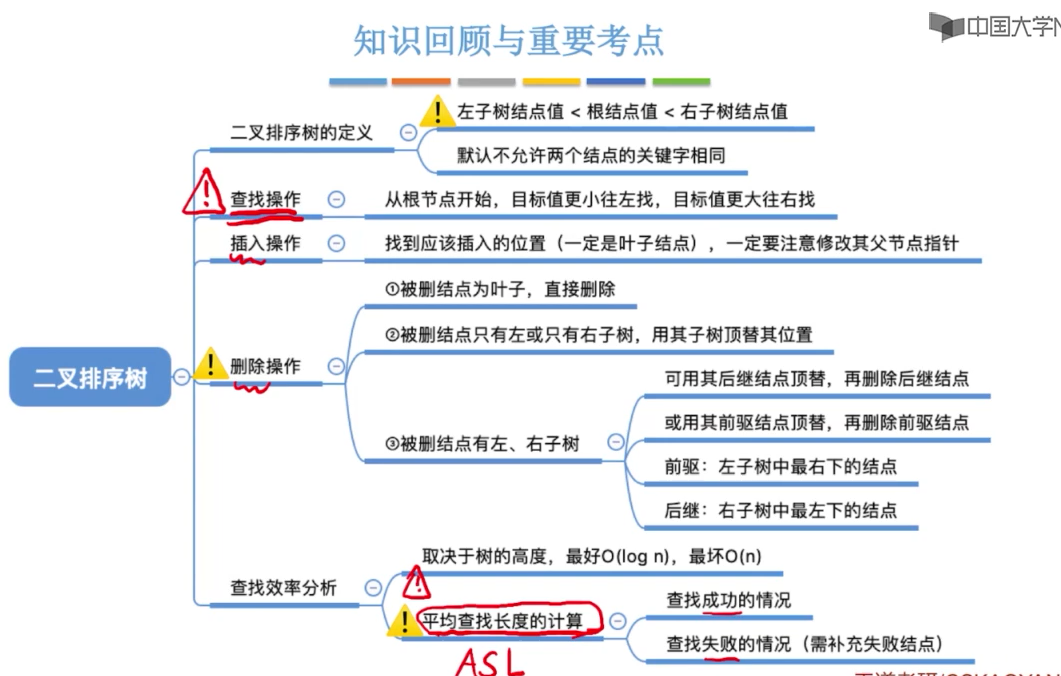
二叉查找树（BST：Binary Search Tree），也称为二叉查找树、有序二叉树（ordered binary tree）或排序二叉树（sorted binary tree），是指一棵空树或者具有下列性质的二叉树：
- 若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
- 若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
- 任意节点的左、右子树也分别为二叉查找树；
二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低。二叉查找树是基础性数据结构，用于构建更为抽象的数据结构，如集合、多重集、关联数组等。
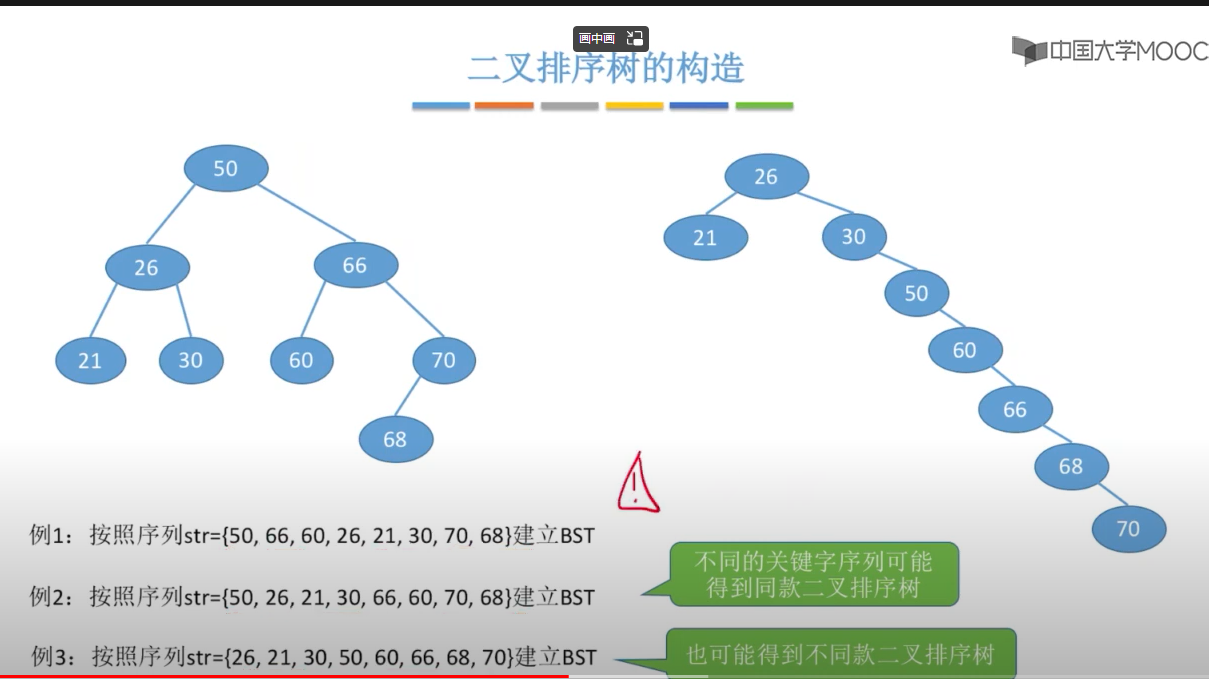
1、对二叉树进行中序遍历，可以得到一个递增的有序序列，这个就是二叉搜索树。所有二叉树排序树是中序遍历二叉树。
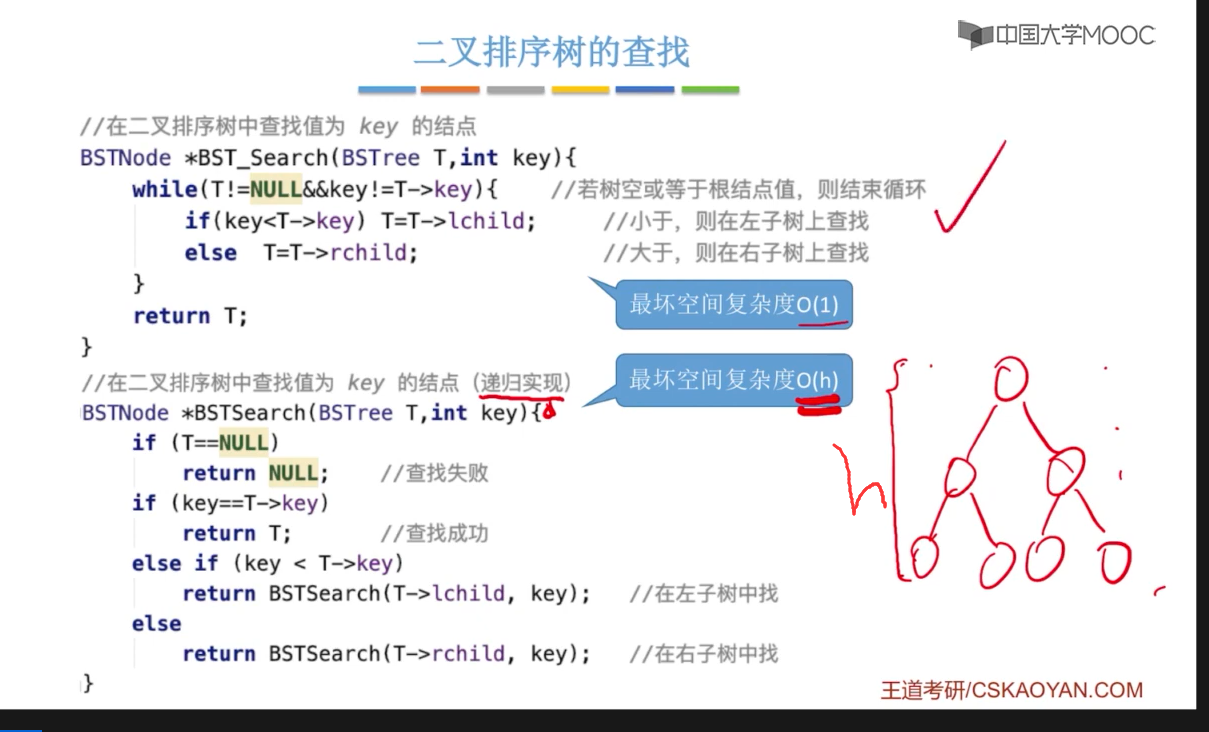
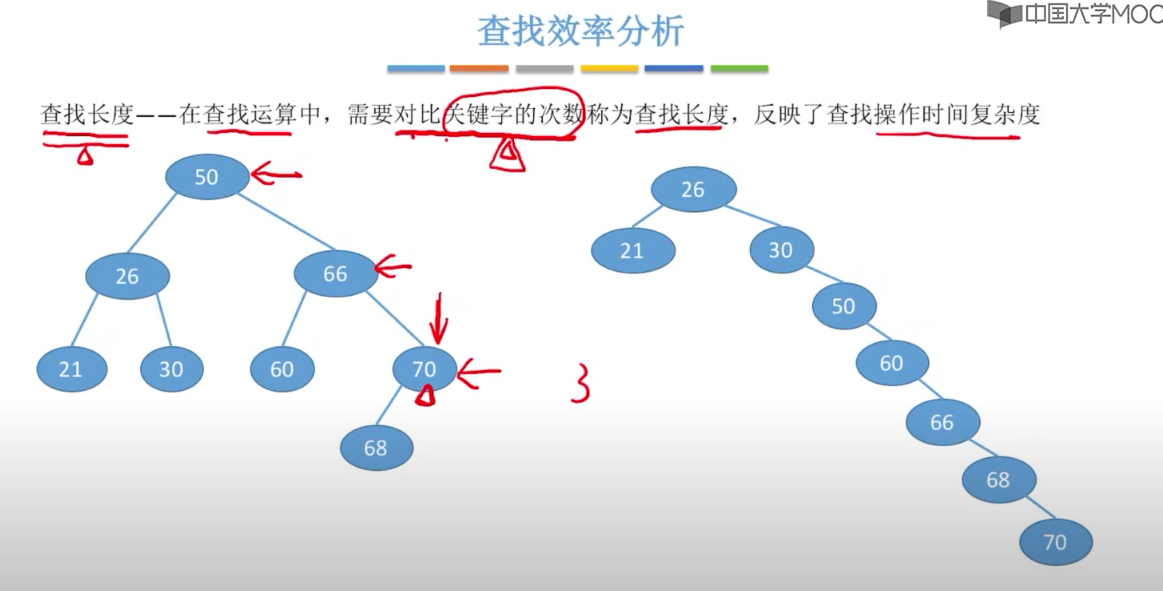
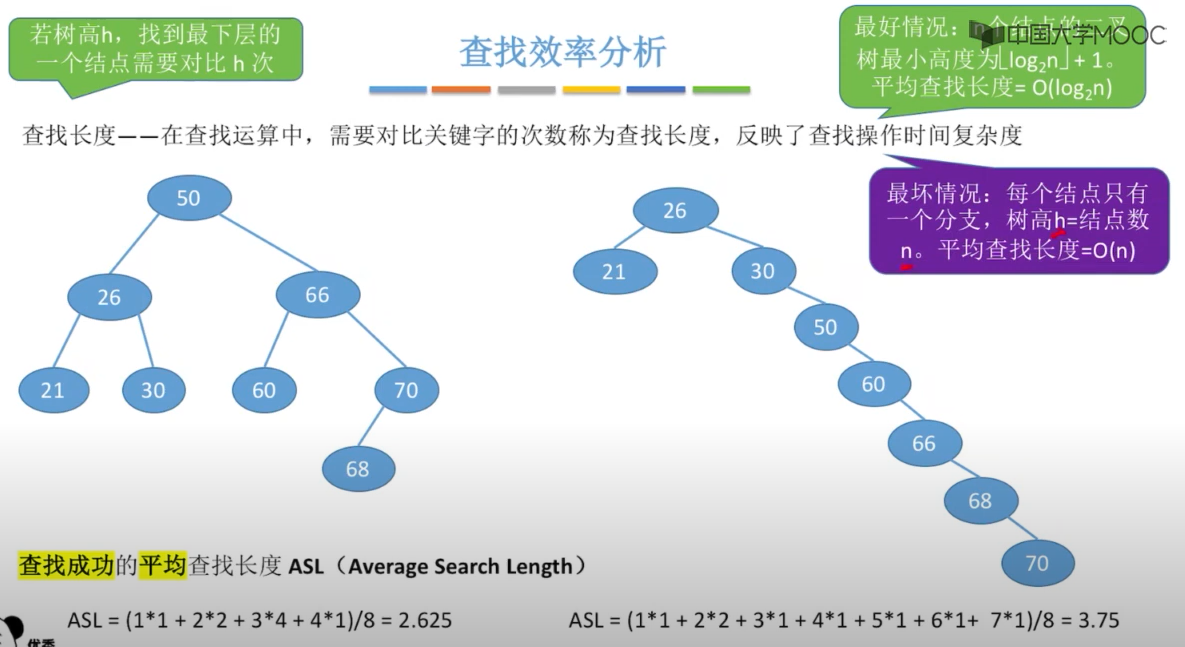
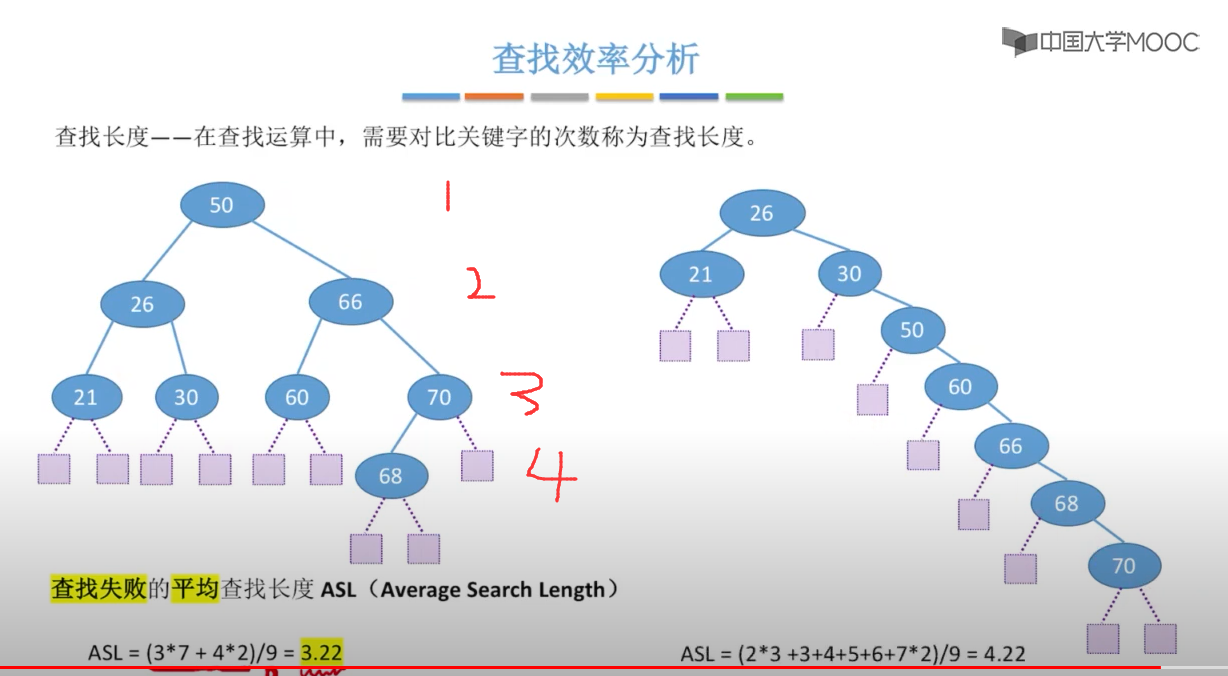
优点：二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低。 搜索、插入、删除的复杂度等于树高，期望 O ( log2n ) ，最坏退化为偏斜二叉树 O ( n ) 。
作用：二叉查找树是基础性数据结构，用于构建更为抽象的数据结构，如集合、多重集、关联数组等。
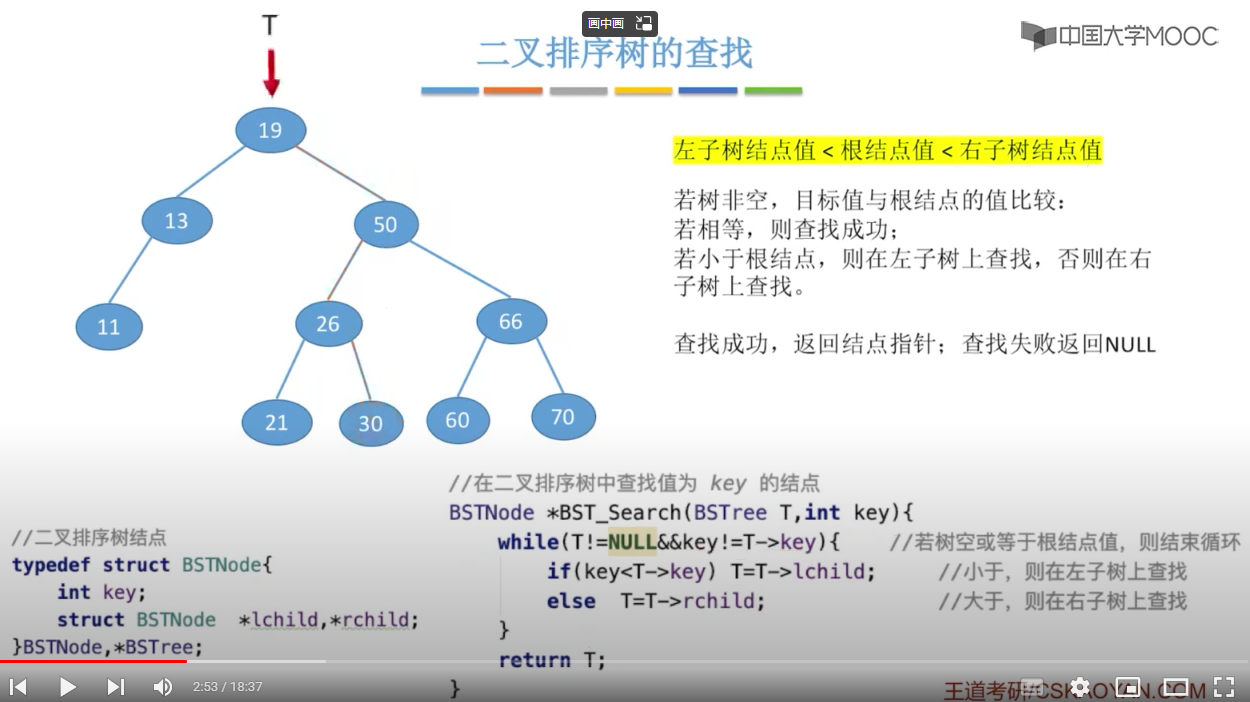
。二叉查找树是基础性数据结构，用于构建更为抽象的数据结构，如存储结构
存储结构：通常采取二叉链表作为二叉查找树的存储结构
改进：对于可能形成偏斜二叉树的问题可以经由树高改良后的平衡树将搜索、插入、删除的时间复杂度都维持在 O ( log2n ) ，如AVL树、红黑树等
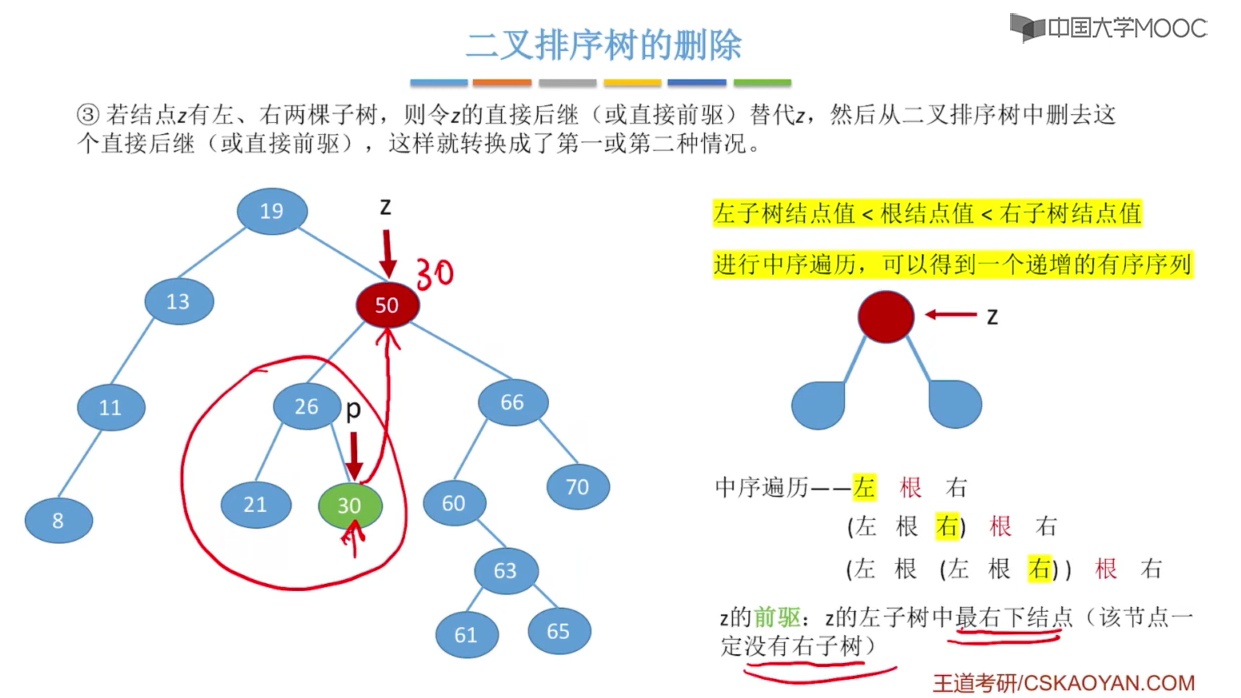
注意：在删除拥有左右子树的Z节点时，要用右子树的中序遍历的 z的后继:z的右子树中最左下结点（该节点一定没有左子树),这样才能保证二叉树的特性不变。
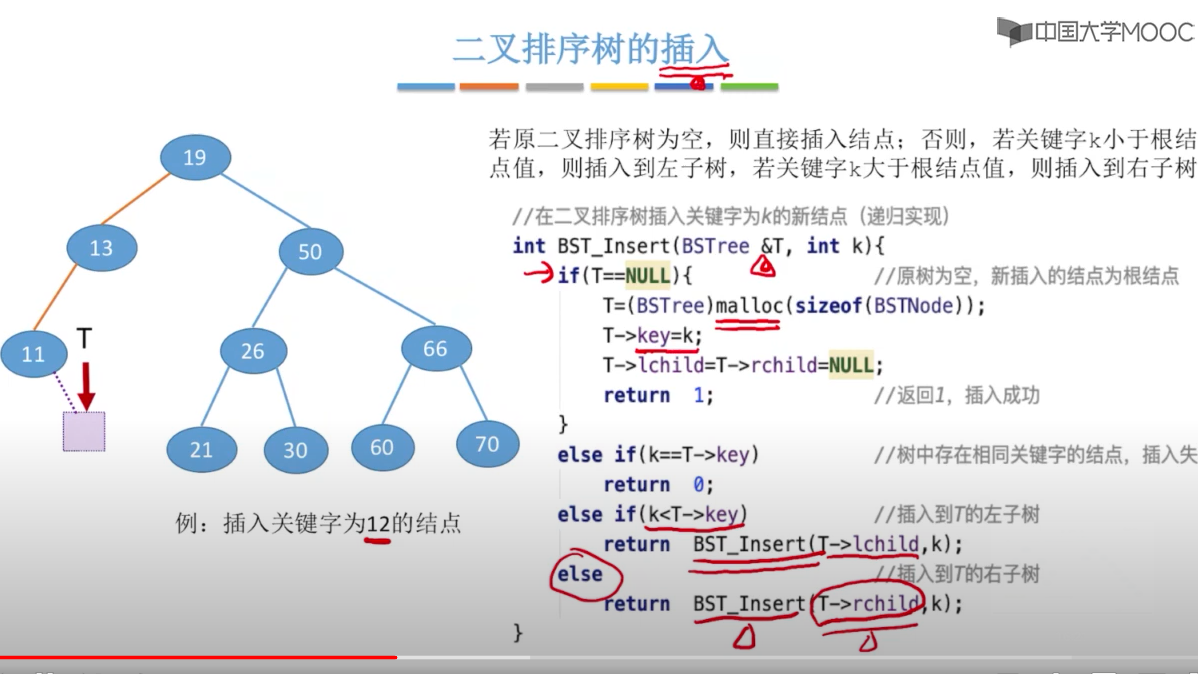
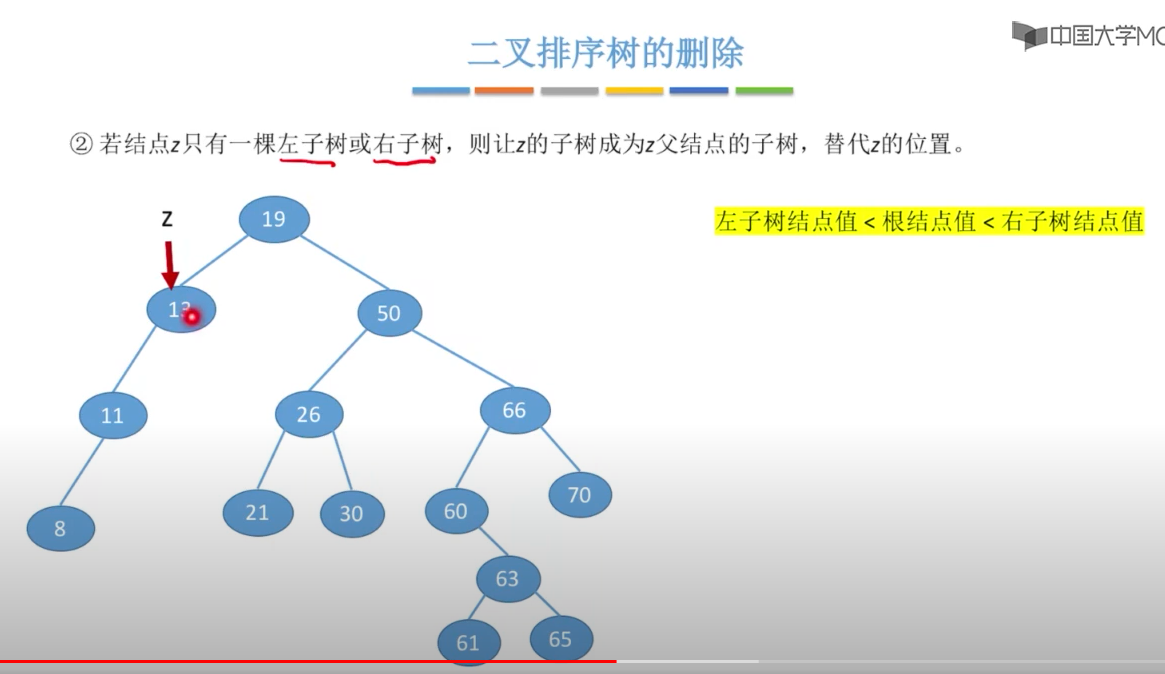
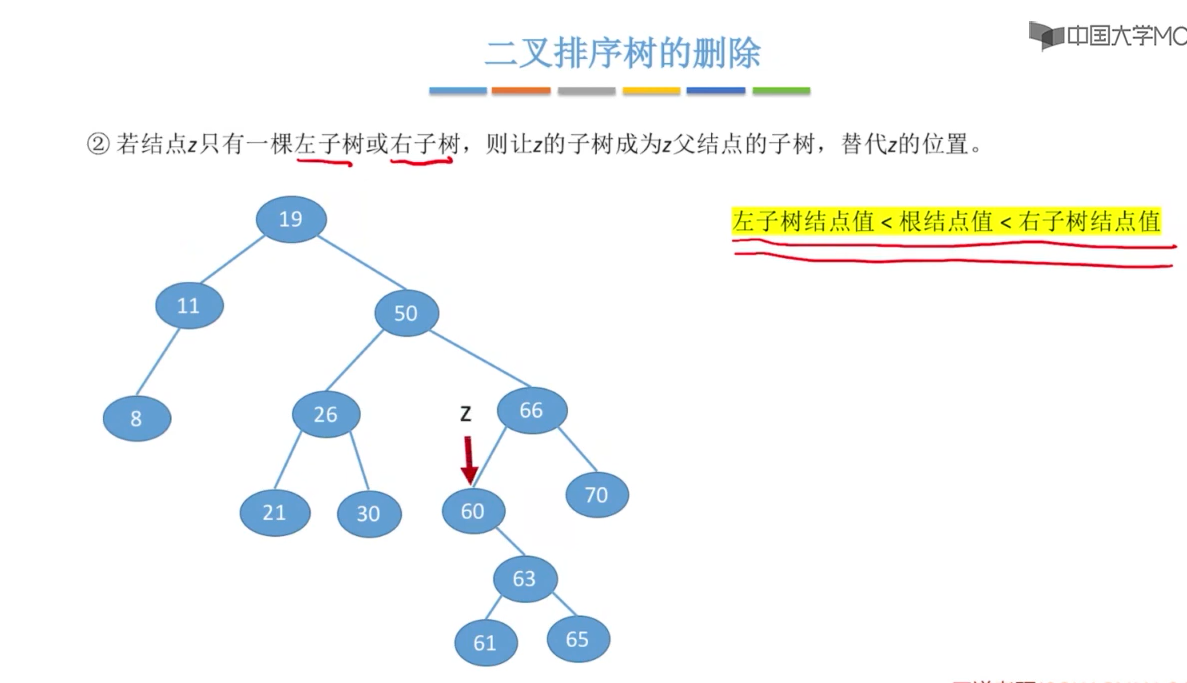
删除后使用后继来替代。
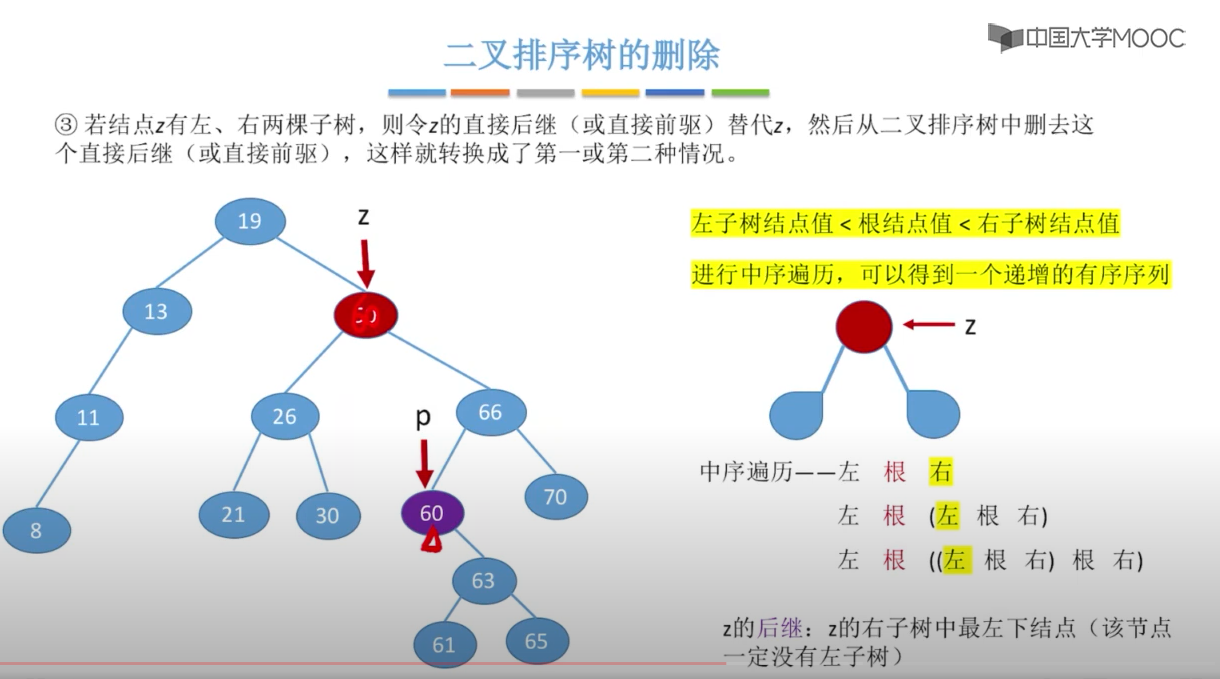
注意：在删除拥有左右子树的Z节点时，要用右子树的中序遍历的 z的后继:z的右子树中最左下结点（该节点一定没有左子树),这样才能保证二叉树的特性不变。
删除后使用前驱来替代
关于算法的时间复杂度很多都用包含O(logN)这样的描述，但是却没有明确说logN的底数究竟是多少。
解答：
算法中log级别的时间复杂度都是由于使用了分治思想,这个底数直接由分治的复杂度决定。
如果采用二分法,那么就会以2为底数,三分法就会以3为底数,其他亦然。
不过无论底数是什么,log级别的渐进意义是一样的。
也就是说该算法的时间复杂度的增长与处理数据多少的增长的关系是一样的。
我们先考虑O(logx(n))和O(logy(n))，x!=y，我们是在考虑n趋于无穷的情况。
求当n趋于无穷大时logx(n)/logy(n)的极限可以发现，极限等于lny/lnx，也就是一个常数，
也就是说，在n趋于无穷大的时候，这两个东西仅差一个常数。
所以从研究算法的角度log的底数不重要。
最后，结合上面，我也说一下关于大O的定义（算法导论28页的定义），
注意把这个定义和高等数学中的极限部分做比较，
显然可以发现，这里的定义正是体现了一个极限的思想，
假设我们将n0取一个非常大的数字，
显然，当n大于n0的时候，我们可以发现任意底数的一个对数函数其实都相差一个常数倍而已。
所以书上说写的O（logn）已经可以表达所有底数的对数了，就像O(n^2)一样。
没有非常严格的证明，不过我觉得这样说比较好理解，如果有兴趣证明，完全可以参照高数上对极限趋于无穷的证明。
