【C# 数据结构】二叉树

 

概览：

 

满二叉树

满二叉树。一棵高度为h（从0开始，root=0），且含有2^h+1-1个结点的二叉树

 

 

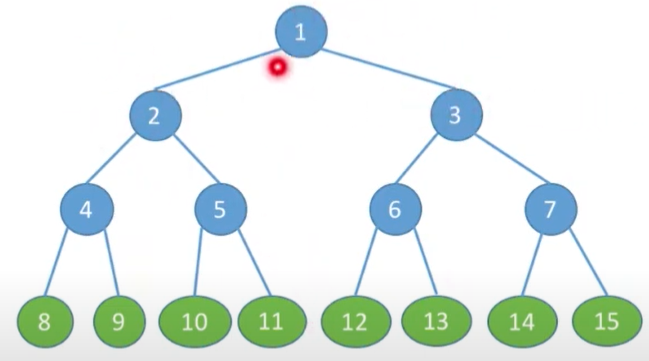
特点:
①只有最后一层有叶子结点

②不存在度为1的结点
③按层序从0开始编号，结点i的左孩子为2i+1，右孩子为2i+2:结点i的父节点为i=0,是根结点无父结点，i！=0，父结点parent=[(i-1)/2|

完全二叉树

完全二叉树。当且仅当其每个结点都与高|深度为h的满二叉树中编号为1～n的结点一一对应时，称为完全二叉树

 

 

 

特点:
①只有最后两层可能有叶子结点

②最多只有一个度为1的结点

③同左③

性质

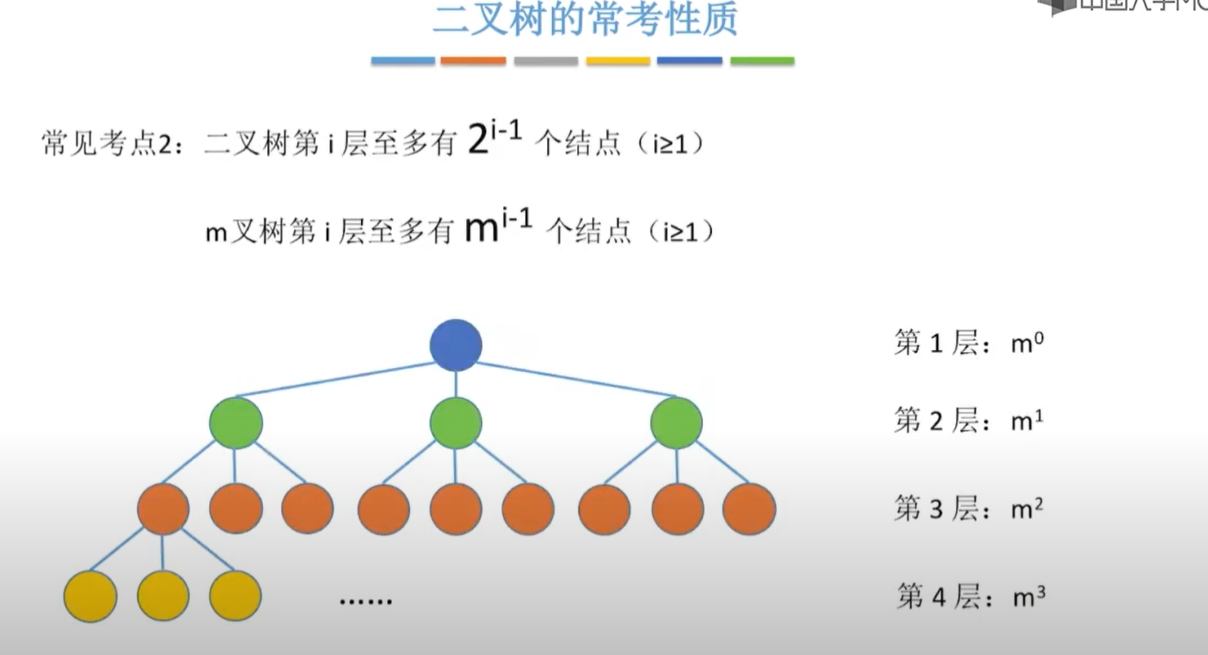
(1) 二叉树第i层的节点数最多为2ⁱ  (i>=0).

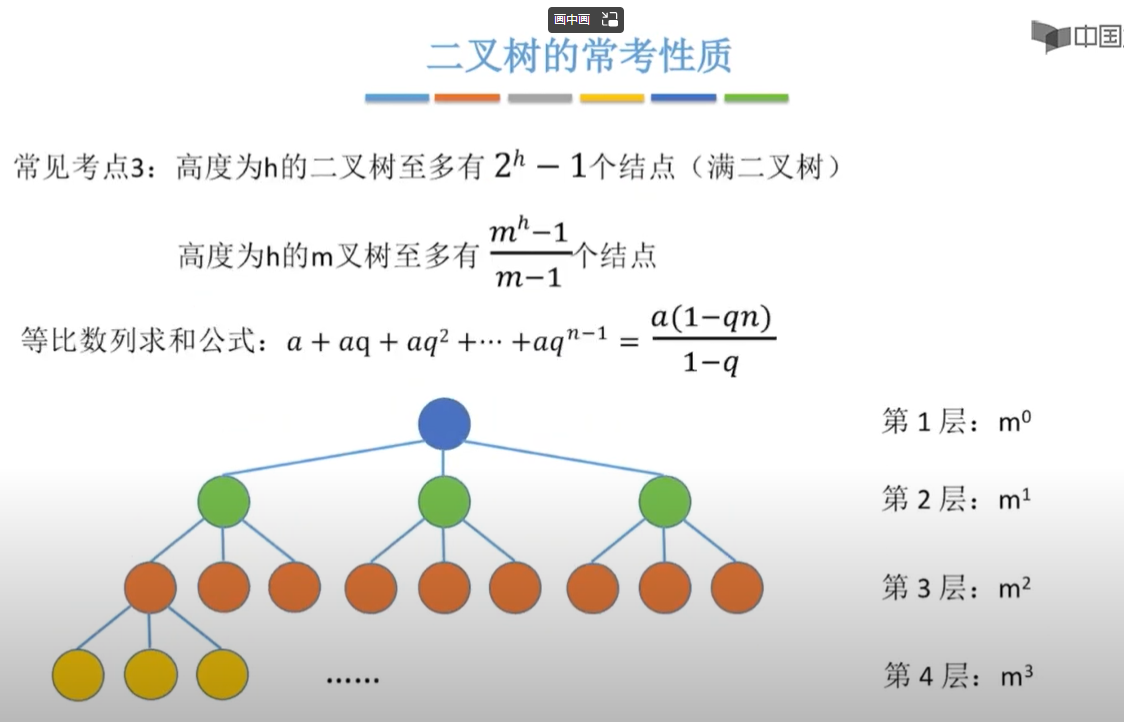
(2)在深|高度为k的二叉树中，最大的节点数为2^k+1-1

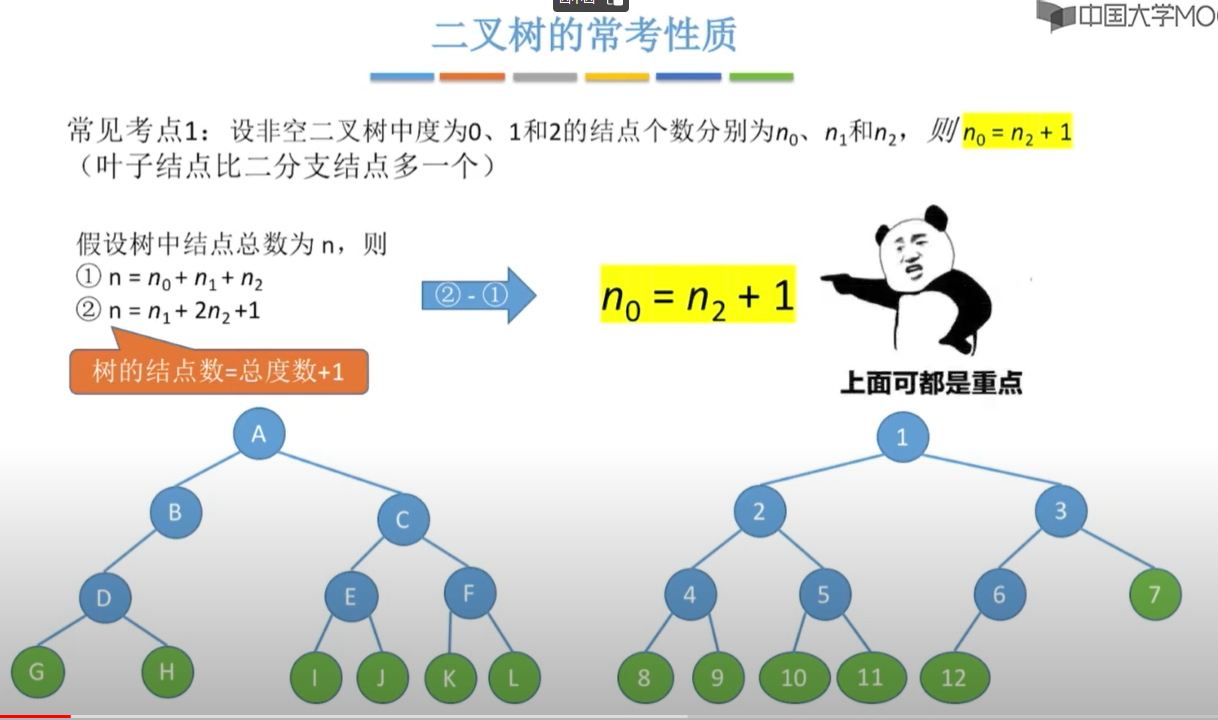
(3）在二叉树中叶子节点数n₀比分支节点数n₁多1：即 n₀=n_{2+1=边数-结点数}

            =>n₀+n₂=2n₂+1 一定是奇数

          =》 节点数：n=n0+n1+n2  边数：n-1=n1+2*n2

(4)如果一颗完全二叉树有n个结点，起高|深度结点的完全二叉树的高度k=[log₂ⁿ], k>=0（[]表示取整）

(5)若将一个具有n个节点的完全二叉树的所有结点按自上而下，自左至右的顺序编号，结点编号i的取值范围为（0<=i<=n-1）,则结点编号存在以下规律：

若i=0,则结点i为根结点，无父结点；若i！=0，则结点i的父结点是编号为j=[(i-1)/2]的结点。

若2i+1<=n-1,则i的左子结点编号为2i+1，若2i+1>n-1，则结点i无左子结点。

若2i+2<=n-1,则i的左子结点编号为2i+2，若2i+2>n-1，则结点i无右子结点。

 (6)n个节点 共有n+1个空指针域  。推理过程=2n-（n-1）2n是所有指针域，n-1是出根结点外，其他节点都有前驱结点。

 

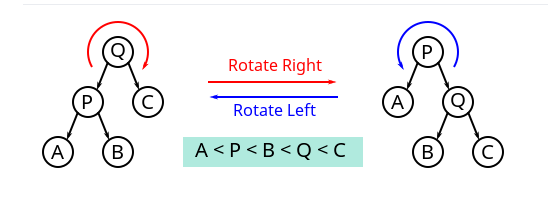
 操作

二叉树常用操作旋转（rotate），该操作为常数时间复杂度。 二叉树旋转前后，中序遍历的结果不变。因此树的任何部分旋转，对整棵树的元素顺序没有影响。

在哈夫曼树中用到。

 

 

 

 

 

 

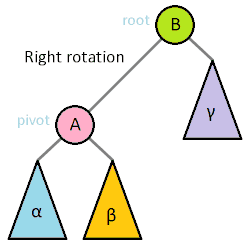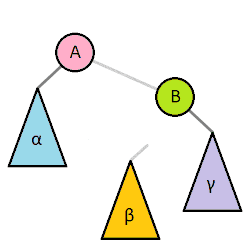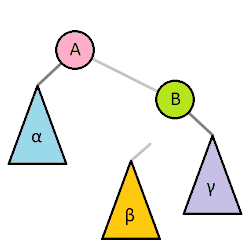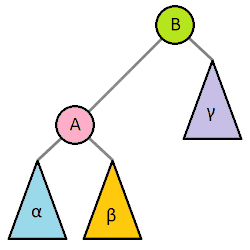
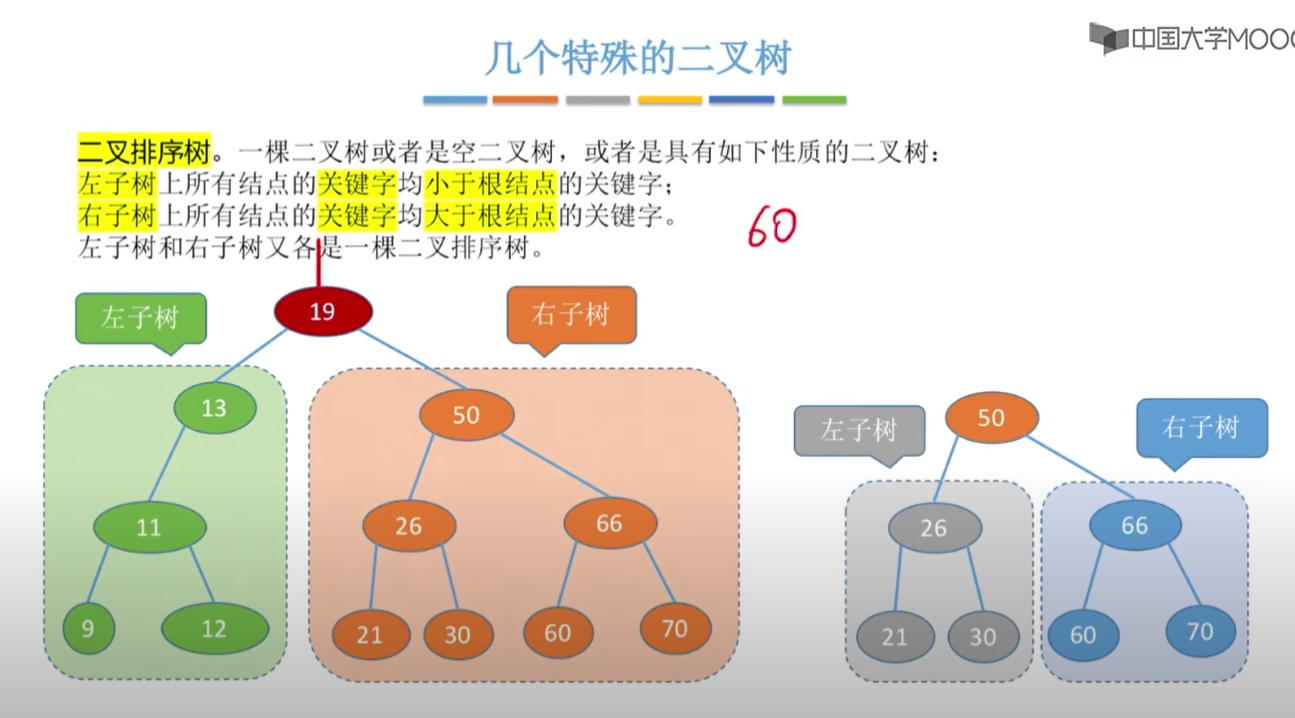
 二叉排序树

 

 

 

 

 

 

 

C#自定义二叉树递归遍历

 

using System;
using System.Diagnostics;
using System.Diagnostics.CodeAnalysis;
using System.Drawing.Drawing2D;
using System.IO;
using System.Text;
using System.Threading;
using System.Xml;
using System.Xml.XPath;
namespace LinearList;
public class Sample
{
    public static void Main()
    {
        LineBinaryTree<int> tree = new(0);
        TreeNode<int>[] nodes=new TreeNode<int> [7];
        for (int i = 0; i < 7; i++)
        {
            nodes[i] = new TreeNode<int>(i);

        }
        tree.Root = nodes[0];
        nodes[0].LeftNode=nodes[1];
        nodes[0].RightNode=nodes[2];
        nodes[1].LeftNode=nodes[3];
        nodes[1].RightNode=nodes[4];
        nodes[2].LeftNode=nodes[5];
        nodes[2].RightNode = nodes[6];
        tree.PreorderTraversal(tree.Root);
        Console.WriteLine();
        tree.MidTraversal(tree.Root);
        Console.WriteLine();
        tree. PostTraversal(tree.Root);


    }
    public class TreeNode<T>
    {
        public TreeNode(T it)
        {
            item = it;
            leftNode = null;
            rightNode = null;
         
        }
        private T? item;

        public T Item { get => item; set => item = value; }
        public TreeNode<T>? LeftNode { get => leftNode; set => leftNode = value; }
        public TreeNode<T>? RightNode { get => rightNode; set => rightNode = value; }
 

        TreeNode<T>? leftNode, rightNode;
 


        public TreeNode()
        {

            item = default;
            leftNode = null;
            rightNode = null;
    

        }
        public void Print()
        {
            Console.WriteLine(Item);
        }
    
    }
    public class LineBinaryTree<T>
    {

        private TreeNode<T>? root ;
   

        public TreeNode<T>? Root { get => root; set => root = value; }
        

        public LineBinaryTree()
        {

        }
        public LineBinaryTree(T it)
        {
            Root = new TreeNode<T>(it);
     
        }

        /// <summary>
        /// 先序遍历
        /// </summary>
        /// <param name="node"></param>
        public void PreorderTraversal(TreeNode<T> node)
        {
            Console.Write(node.Item + "=>");

            if (node.LeftNode != null)
                PreorderTraversal(node.LeftNode);

            if (node.RightNode != null)
                PreorderTraversal(node.RightNode);
 


        }
        /// <summary>
        /// 中序遍历
        /// </summary>

        public void MidTraversal(TreeNode<T> node)
        {
          
            if (node.LeftNode != null)
                MidTraversal(node.LeftNode);
            Console.Write(node.Item + "=>");
            if (node.RightNode != null)
                MidTraversal(node.RightNode);
         


        }
        /// <summary>
        /// 后序遍历
        /// </summary>
        public void PostTraversal(TreeNode<T> node)
        {

            if (node.LeftNode != null)
                PostTraversal(node.LeftNode);

            if (node.RightNode != null)
                PostTraversal(node.RightNode);
            Console.Write(node.Item + "=>");


        }
    }
}