【C# 数据结构与算法】二元组---逻辑结构的
多元组
多元组，也称为顺序组（英语：Tuple），泛指有限个元素所组成的序列。在数学及计算机科学分别有其特殊的意义。
数学上，n元组或多元组是对象个数有限的序列。元组由三部分组成：边界符、分隔符和元素。通常采用的边界符是小括号“
”，分隔符是逗号。 多元组被数学家用来描述包含特定部件的数学对象。例如，有向图被定义成一个二元组（V, E），这里V是节点的集合，E是V × V的子集，表示边。
多元组的名称
长度为n的多元组通常称为n元组。二元组就是一个有序对。n可以是任意正整数，例如，四元数就可以被表示成一个四元组。
二元组表示法
对于数据的逻辑结构还有一种二元组表示法，下面是二元组表示方法。
逻辑结构二元组表示方法：B = （D , R）
B——数据结构
D——数据元素的集合
R——D上二元关系的集合
在上面这种二元组表示方法中，B就是一种数据结构， 用上面的二元组来表示B这种数据结构时，就是由数据元素的集合D和D中的二元关系的集合R组成的，通过这句话，我们可以明白：
D=di|1≤i≤n,n≥0， 数据元素的集合
表示的是集合D中第i个节点或数据元素，换句话说，数据元素的集合D就是由多个组成的。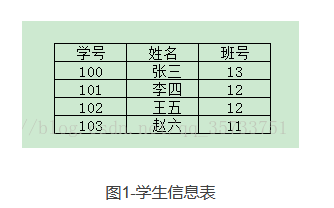
图1-学生信息表
如图1所示，每一个同学的信息（学号，姓名，班号）都是一个数据元素，也就是说，数据元素的结合D包括了图中的每一位同学，而则表示图中的第i个同学的信息。另外，我们知道学号是具有唯一性，且不会重复，因此我们在抽取数据集合时，可以用学号来代表每一位同学的信息（学号，姓名，班号）。
n表示了数据元素的集合D中节点或元素的个数，如果n为0则说明D中节点或元素个数为0，D是一个空集。
R=rj|1≤j≤m,m≥0， D上二元关系的集合
R代表了D上二元关系的集合，这个二元关系是表示上图中（数据元素的集合D中）的两两元素之间的关系，比如：100和101这两个数据元素之间的关系就是一个二元关系，101和102也是如此。也就是说，集合R中有多个二元关系。
表示了集合R中的第j个二元关系，且每个关系用序偶表示。
序偶表示方法： <script type="math/tex" id="MathJax-Element-69"> </script>， ，括号中的x，y两个元素之间的关系就是一个二元关系。
x为第一个元素，y为第二个元素，x为y的前驱元素，y为x的后继元素
对于开始元素来说，没有前驱元素节点；对于终端元素来说，没有后继元素节点。
<script type="math/tex" id="MathJax-Element-71"> </script> 代表有向关系，也就是说x为第一，y为第二；而 代表无向关系，也就是说没有前后之分，第一和第二之分。因此我们可以知道 就是由若干个这样的序偶来表达的。
对于m来说，m表示了集合R中二元关系的个数，如果m = 0，表示二元关系的集合R是一个空集，R是一个空集的话就说明了集合D中元素间是独立的，不存在任何关系，对这种关系只要了解即可。我们在学习数据结构时应该关注有结构的，彼此之间有关系的数据是如何组织的。
我们根据上面所描述知道了二元组的表示方法，那么再对于学生表的逻辑结构二元组表示，如下所示：
学生表 = （D，R）
D = {100，101，102，103}
R = {r}
r = {<100，101>，<101，102>，<102，103>}
我们从D上二元关系的集合R中可以知道它们的关系是一个有向关系，具体关系如r中的所示：在<100，101>序偶中100为第一个数据元素，101为第二个数据元素，其他以此类推，不难看出元素之间是两两相邻的关系，最终它们形成的结构就是一个线性结构，如下所示：
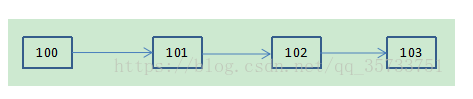
图2-学生表的逻辑结构
2. 逻辑结构的二元组表示法
现在我们来看一个例子，根据逻辑结构来画出其二元组表示法。在图3中一个矩阵，数据如下：
图3-矩阵的逻辑结构
对应的逻辑结构二元组表示如下：
B = {D，R} D = {2，6， 3 ，1 ，8 ，12 ， 7 ，4 ，5 ，10 ，9 ，11} R = {r1 ，r2} （r1表示行关系，r2表示列关系） r1 = {<2，6>，<6，3>，<3，1>，<8，12>，<12，7>，<7，14>，<5，10>，<10，9>，<9，11>}（行关系） r2 = {<2，8>，<8，5>，<6，12>，<12，10>，<3，7>，<7，9>，<1，4>，<4，11>}（列关系）
D表示了数据元素的集合，而D的大括号中的就是数据元素，而R表示了D上二元关系的集合，也就是在二元关系的集合R中有r1和r2这两个二元关系，其中r1代表行关系，r2代表列关系。
3. 根据二元组画出逻辑结构
在应用过程中，当给出二元组这种抽象的表示方法之后，我们应该做到能够根据这种抽象的二元组表示法中给出的信息，用逻辑结构图画出来，通过逻辑结构更加直观的判断具体属于哪一种数据结构。
3.1 例1
二元组表示法如下：
B1 = （D，R） D = {a，b，c，d，e，f，g，h，i，j} R = {r} r = { <a，b>，<a，c>，<a，d>，<b，e>，<c，f>，<c，g>，<d，h>，<d，i>，<d，j> }
从它的二元关系的序偶 <script type="math/tex" id="MathJax-Element-11"></script> 中可以看出这是一个有向关系，那么其二元组关系对应的逻辑结构如下图所示：
图4-逻辑结构1
3.2 例2
二元组表示如下：
B2 = （D，R） D = {a，b，c，d，e} R = {r} r = { (a，b)， (a，c)， (b，c)， (c，d)， (c，e)， (d，e) }
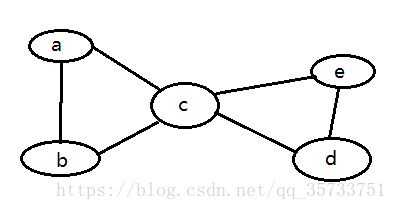
图5-逻辑结构2
3.3 例3
二元组表示如下：
B3 = （D，R） D = {48，25，64，57，82，36，75} R = {r1 ， r2} r1 = {<48，25>，<48，64>，<64，57>，<64，82>，<25，36>，<82，75>} r2 = {<25，36>，<36，48>，<48，57>，<57，64>，<64，57>，<75，82>}
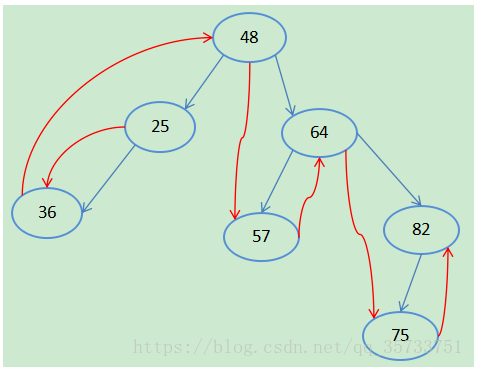
图6-逻辑结构3
在图6中r1关系如蓝色箭头所示，r2关系如红色箭头所示。
