由浅入深!一文带你彻底明白堆排序
本文中所有的代码全都是大根堆!实现语言是Java
图片来源都是这位大神的,大神的文章也给了我很多启发
什么是堆
1.堆的概念
如果有一个关键码的集合K = {k0,k1, k2,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足:Ki <= K2i+1 且 Ki<=K2i+2 ,则称为小堆(或大堆)。
将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
2.性质
-
堆是一颗完全二叉树
-
堆中的某个结点不大于或不小于其父节点的值

3.二叉树和堆的关系
既然知道了堆在逻辑结构上符合完全二叉树的性质,那么堆就符合完全二叉树的性质,这里有两个性质堆接下来的学习很重要!!
在堆中,cur代表当前节点的下标,parent代表其父节点下标,child1,child2代表其两个子节点下标,那么满足
-
parent = (cur - 1) / 2
-
child1 = 2 * i + 1
-
child2 = 2 * i + 2
如何实现堆?
知道了堆是由数组构成的,那么数组如何变成我们想要的堆呢?这里就提出了一种方法堆化!
heapify堆化,一种将数组转换为堆的算法!其他的博文也把它叫做向上调整算法算法、向下调整算法。
向上调整算法是基于向下调整算法的,所以要想明白向上调整必须先明白什么是向下调整,这也是难点!
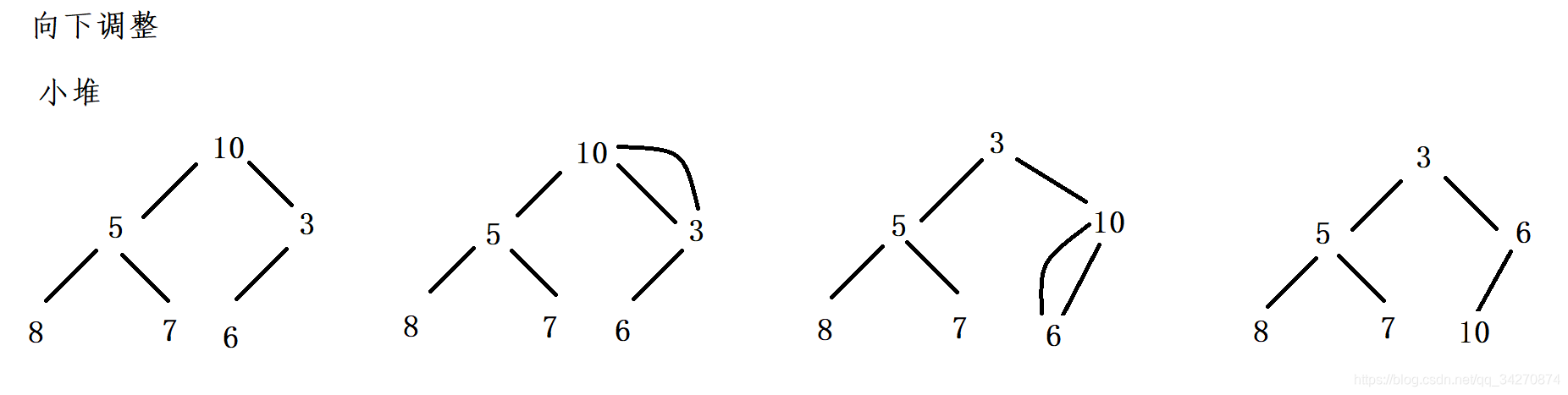
向下调整算法原理
-
设定根节点为当前节点(通过下标获取,标记为cur),比较左右子树的值,找出更小的值,用child来标记。
-
比较child和cur的值,如果child比cur小,则不满足小堆的规则,需要进行交换。
-
如果child比cur大,满足小堆的规则,不需要交换,调整结束。
-
处理完一个节点之后,从当前的child出发,循环之前的过程。
向下调整算法是基于原本的堆因为插入元素导致不是堆而做出调整的算法
图中的例子也可以看出587是堆
向上调整算法原理
-
先设定倒数的第一个叶子节点为当前节点(通过下标获取,标记为cur),找出他的父亲节点,用parent来标记。
-
比较parent和cur的值,如果cur比parent小,则不满足小堆的规则,需要进行交换。
-
如果cur比parent大,满足小堆的规则,不需要交换,调整结束。
-
处理完一个节点之后,从当前的parent出发,循环之前的过程。
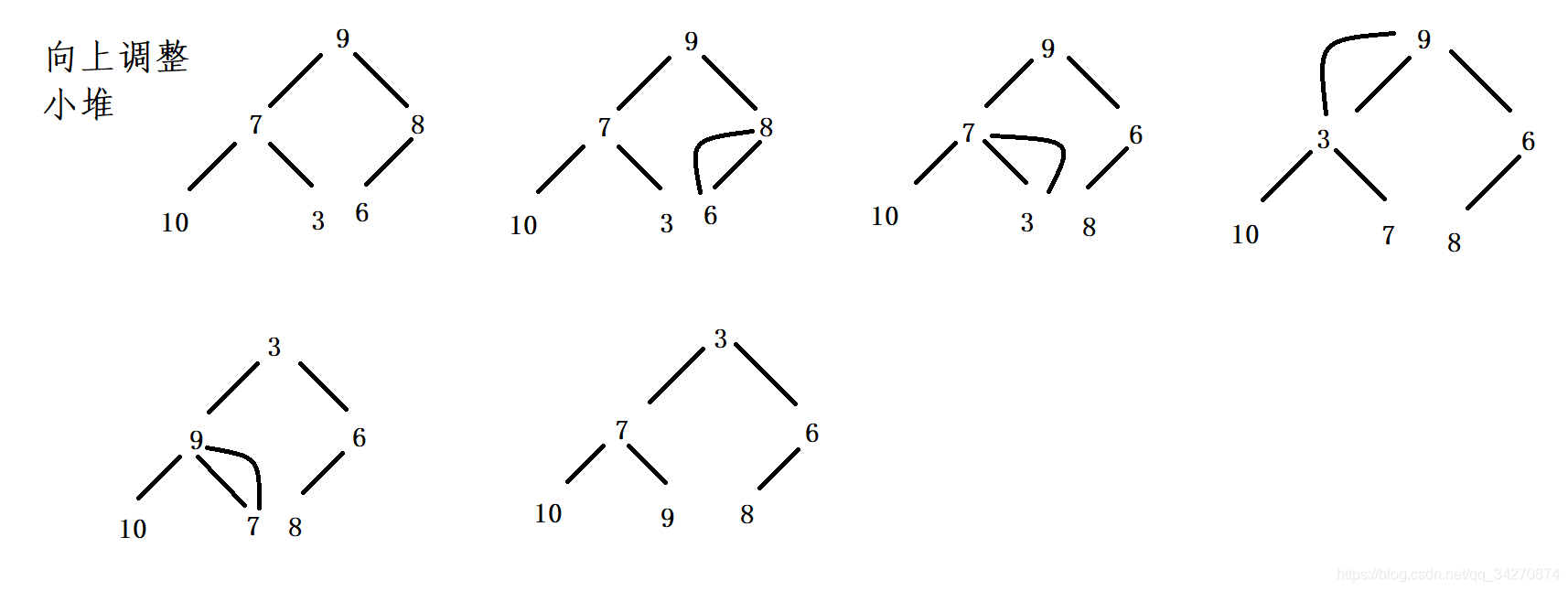
上文说到向上调整算法是基于向下调整算法实现的!为什么这么说呢?因为向上调整的过程是将二叉树分割成最小单元(这里的最小单元是指由一个根节点零到两个的孩子节点构成的最小二叉树),从下往上对每一个最小二叉树做向下调整算法。当对所有的最小二叉树做完向下调整算法后也就完成了堆化!
明白什么是堆化以后我们来动手实现一下,这里用到的是递归的方法
递归这里有点难理解我单独说一下,因为我们是将数组传进来,第一次遍历的i代表的是堆的最顶部的元素,从上到下直到碰到叶子节点就结束了
/**
* 交换两个值,注意这里不能使用位运算来交换,因为会导致数组首个元素为0的情况
*
* @param array 数组
* @param i 第一个值
* @param j 第二个值
*/
public static void swap(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
//堆化是由向上调整算法和向下调整算法构成的
/**
* 向下调整算法
*
* @param tree 存储结构上为数组,逻辑结构上为完全二叉树
* @param size 数组长度
* @param i 父节点
*/
public static void heapify(int[] tree, int size, int i) {
//记录父节点方便后续交换
int max = i;
//父节点的两个子节点
int child1 = 2 * i + 1;
int child2 = 2 * i + 2;
//如果左孩子大于父节点那么记录左孩子结点
if (child1 < size && tree[child1] > tree[max]) {
max = child1;
}
//如果右孩子大于父节点或者是左节点(上一个if判true记录了左孩子)那么记录右孩子
if (child2 < size && tree[child2] > tree[max]) {
max = child2;
}
if (max != i) {
swap(tree, max, i);
heapify(tree, size, max);
}
}
/**
* 向上调整算法 将无序数组构建成堆
*
* @param tree 数组
* @param size 数组大小
*/
public static void buildHeap(int[] tree, int size) {
//从下往上调整算法,从最后一个节点开始
int lastNode = size - 1;
//该节点的父节点
int parent = (lastNode - 1) / 2;
for (int i = parent; i >= 0; i--) {
//对每一个最小单元做向下调整算法
heapify(tree, size, i);
}
}
不理解递归也不关系这里有迭代的
public static void heapify(int[] tree, int size, int i) {
//当前节点的左右孩子
int child1 = 2 * i + 1;
int child2 = 2 * i + 2;
//遍历到叶子节点了也就结束了
while (child1 < size) {
int max = i;
//如果左孩子大于父节点那么记录左孩子结点
if (child1 < size && tree[child1] > tree[max]) {
max = child1;
}
//如果右孩子大于父节点或者是左节点(上一个if判true记录了左孩子)那么记录右孩子
if (child2 < size && tree[child2] > tree[max]) {
max = child2;
}
//如果父结点索引是最大值的索引,那已经是大根堆了,则退出循环
if (i == max) {
break;
}
//父结点不是最大值,与孩子中较大的值交换
swap(tree, max, i);
//将索引指向孩子中较大的值的索引
i = max;
//重新计算交换之后的孩子的索引
child1 = 2 * i + 1;
child2 = 2 * i + 2;
}
}
明白堆化(向下调整)以后相信你对堆的感觉越来越接近了
堆排序
明白了堆的构建过程后,堆排序简直不要太简单,直接讲算法实现原理
-
将待排序序列构造成一个大根堆
-
此时,整个序列的最大值就是堆顶的根节点。
-
将其与末尾元素进行交换,此时末尾就为最大值。
-
然后将剩余n-1个元素重新构造成一个堆,这样会得到n-1个元素的次小值。如此反复执行,便能得到一个有序序列了。

这里贴出完整代码
/**
* 堆排序
*
* @author ccy
* @version 1.0
* @date 2021/11/20 15:11
*/
public class HeapSort {
/**
* 交换两个值,注意这里不能使用位运算来交换,因为会导致数组首个元素为0的情况
*
* @param array 数组
* @param i 第一个值
* @param j 第二个值
*/
public static void swap(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
//堆化是由向上调整算法和向下调整算法构成的
/**
* 向下调整算法
*
* @param tree 存储结构上为数组,逻辑结构上为完全二叉树
* @param size 数组长度
* @param i 父节点
*/
public static void heapify(int[] tree, int size, int i) {
//记录父节点方便后续交换
int max = i;
//父节点的两个子节点
int child1 = 2 * i + 1;
int child2 = 2 * i + 2;
//如果左孩子大于父节点那么记录左孩子结点
if (child1 < size && tree[child1] > tree[max]) {
max = child1;
}
//如果右孩子大于父节点或者是左节点(上一个if判true记录了左孩子)那么记录右孩子
if (child2 < size && tree[child2] > tree[max]) {
max = child2;
}
if (max != i) {
swap(tree, max, i);
heapify(tree, size, max);
}
}
/**
* 向上调整算法 将无序数组构建成堆
*
* @param tree 数组
* @param size 数组大小
*/
public static void buildHeap(int[] tree, int size) {
//从下往上调整算法,从最后一个节点开始
int lastNode = size - 1;
//该节点的父节点
int parent = (lastNode - 1) / 2;
for (int i = parent; i >= 0; i--) {
//对每一个最小单元做向下调整算法
heapify(tree, size, i);
}
}
/**
* 堆排序
*
