价值迭代 (Value Iteration)
转载自知乎
https://zhuanlan.zhihu.com/p/33229439
假设我们有一个3 x 3的棋盘:
- 有一个单元格是超级玛丽,每回合可以往上、下、左、右四个方向移动
- 有一个单元格是宝藏,超级玛丽找到宝藏则游戏结束,目标是让超级玛丽以最快的速度找到宝藏
- 假设游戏开始时,宝藏的位置一定是(1, 2)
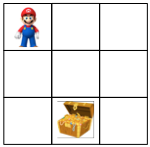
这个一个标准的马尔科夫决策过程(MDP):
- 状态空间State:超级玛丽当前的坐标
- 决策空间Action: 上、下、左、右四个动作
- Action对State的影响和回报 P(State', Reward | State, Action):本文认为该关系是已知的
- 超级玛丽每移动一步,reward = -1
- 超级玛丽得到宝箱,reward = 0并且游戏结束
利用价值迭代 (Value Iteration) 求解马尔科夫决策过程
首先我们定义超级玛丽当前位置的价值 :从当前state = (x, y)开始,能够获得的最大化Reward的总和。
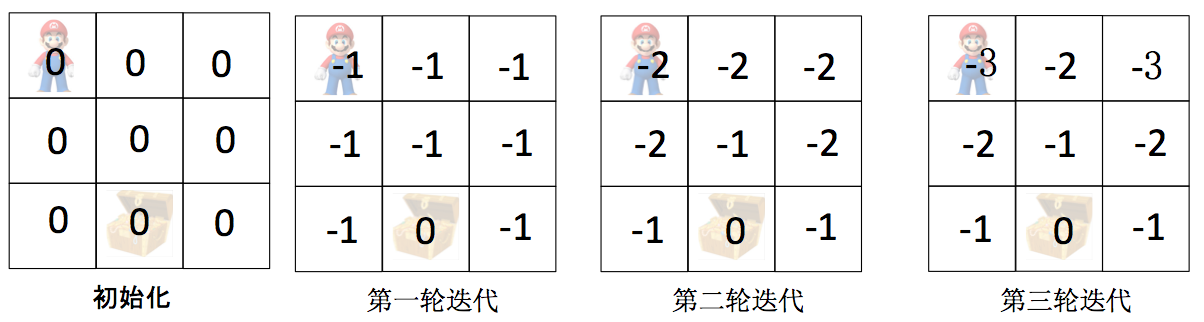
结合上图可以非常简单的理解价值迭代:
- 初始化:所有state的价值V(s) = 0
- 第一轮迭代:对于每个state,逐一尝试上、下、左、右四个Action
- 记录Action带来的Reward、以及新状态 V(s')
- 选择最优的Action,更新V(s) = Reward + V(s') = -1 + 0
- 第一轮结束后,所有状态都有V(s) = -1,即从当前位置出发走一步获得Reward=-1
- 第二轮迭代:对于每个state,逐一尝试上、下、左、右四个Action
- 记录Action带来的Reward、以及新状态 V(s')
- 选择最优的Action,更新V(s) = Reward + V(s')
- 对于宝箱周围的State,最优的Action是一步到达宝箱,V(s) = Reward + V(s') = -1 + 0
- 对于其他State,所有的Action都是一样的,V(s) = Reward + V(s') = -1 + -1
- 第二轮结束后,宝箱周围的State的价值保持不变 V(s) = -1,其他State的价值 V(s) = -2
- 第三轮迭代:对于每个state,逐一尝试上、下、左、右四个Action
- 记录Action带来的Reward、以及新状态 V(s')
- 选择最优的Action,更新V(s) = Reward + V(s')
- 对于宝箱周围的State,最优的Action是一步到达宝箱,V(s) = Reward + V(s') = -1 + 0
- 对于宝箱两步距离的State,最优的Action是先一步到达宝箱周边的State,V(s) = Reward + V(s') = -1 + -1
- 对于宝箱三步距离的State,所有Action都是一样的,V(s) = Reward + V(s') = -1 + -2
- 第四轮迭代:对于每个state,逐一尝试上、下、左、右四个Action
- 记录Action带来的Reward、以及新状态 V(s')
- 选择最优的Action,更新V(s) = Reward + V(s')
- 对于宝箱周围的State,最优的Action是一步到达宝箱,V(s) = Reward + V(s') = -1 + 0
- 对于宝箱两步距离的State,最优的Action是先一步到达宝箱周边的State,V(s) = Reward + V(s') = -1 + -1
- 对于宝箱三步距离的State,最优的Action是所有Action都是一样的,V(s) = Reward + V(s') = -1 + -2
- 在第四轮迭代中,所有V(s)更新前后都没有任何变化,价值迭代已经找到了最优策略
上面的迭代过程实际上运用了贝尔曼方程 (Bellman Equation),对每个位置的价值进行更新
贝尔曼方程 (Bellman Equation)是非常好理解的 --- 状态s的价值V(s)由两部分组成:
- 采取action=a后带来的reward
- 采取action=a后到达的新的状态的价值V(s')
源码实现
下面的代码实现了一个Agent,价值迭代在optimize函数中实现,完整可运行jupyter notebook欢迎访问我的Github: whitepaper/RL-Zoo
class Agent:
def __init__(self, env):
self.env = env
self.V = np.zeros(env.nS)
def next_best_action(self, s, V):
action_values = np.zeros(env.nA)
for a in range(env.nA):
for prob, next_state, reward, done in env.P[s][a]:
action_values[a] += prob * (reward + DISCOUNT_FACTOR * V[next_state])
return np.argmax(action_values), np.max(action_values)
def optimize(self):
THETA = 0.0001
delta = float("inf")
round_num = 0
while delta > THETA:
delta = 0
print("\nValue Iteration: Round " + str(round_num))
print(np.reshape(self.V, env.shape))
for s in range(env.nS):
best_action, best_action_value = self.next_best_action(s, self.V)
delta = max(delta, np.abs(best_action_value - self.V[s]))
self.V[s] = best_action_value
round_num += 1
policy = np.zeros(env.nS)
for s in range(env.nS):
best_action, best_action_value = self.next_best_action(s, self.V)
policy[s] = best_action
return 