5.线性回归算法

1.本节重点知识点用自己的话总结出来，可以配上图片，以及说明该知识点的重要性

回归属于机器学习的监督学习，而回归主要包括线性回归、Logistic回归和回归的评估

 

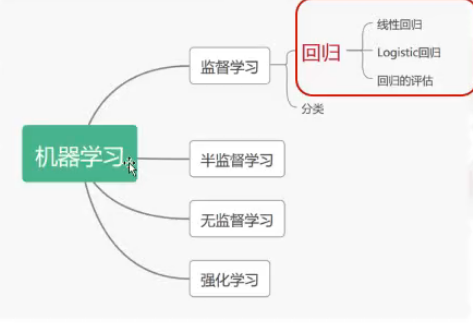
 回归和分类的区别：

分类和回归的区别在于输出变量的类型（预测的目标函数是否连续）。

定量输出成为回归，或者说是连续变量预测。

定性输出称为分类，或者说是离散变量预测。

线性回归

 

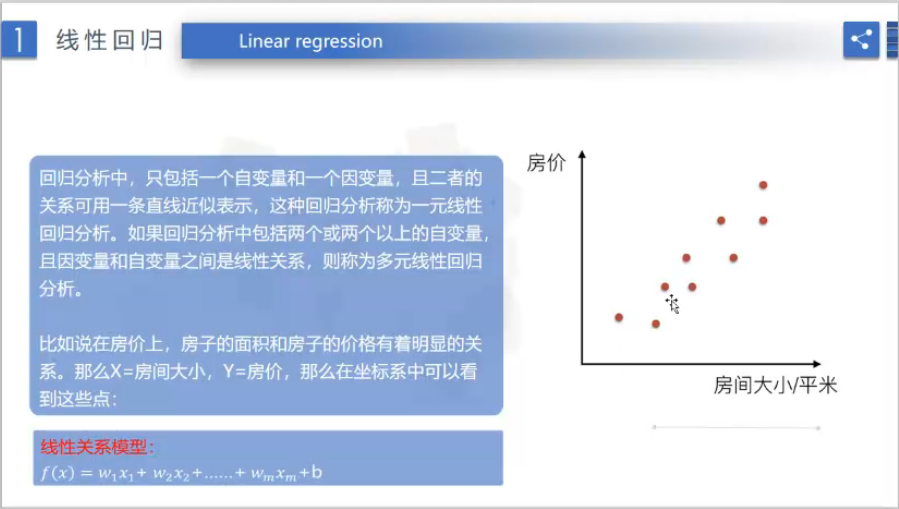
 定义：

线性回归通过一个或者多个自变量与因变量之间进行建模的回归方法，其中可以为一个或者多个自变量之间的线性组合。

 

 矩阵：

大多数算法的计算基础，矩阵的这种运算正好满足了线性回归的这种需求。

损失函数：

 

 

正规方程：

 

 

 

 

 

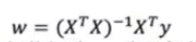
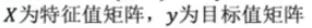
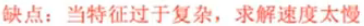
 梯度下降法：

 

 

2.思考线性回归算法可以用来做什么？（大家尽量不要写重复）

        预测某种因素下某事件发生的概率，例如墙体坍塌，与砌墙的材质有关、使用时间有关、承建商有关、外部因素有关等等。

以这些因素来对墙体坍塌的概率进行预测。

3.自主编写线性回归算法 ，数据可以自己造，或者从网上获取。（加分题）

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression  # 线性回归

# 样本数据集，第一列为x，第二列为y，在x和y之间建立回归模型
data=[
    [0.06,3.17],[0.42,3.81],[0.99,4.55],[0.73,4.25],[0.98,4.56],
    [0.52,3.92],[0.37,3.52],[0.03,3.15],[0.13,3.11],[0.13,3.14],
    [0.24,3.47],[0.64,4.11],[0.73,4.28],[0.23,3.48],[0.96,4.65],
    [0.60,3.96],[0.35,3.51],[0.14,3.12],[0.63,4.09],[0.23,3.47],
    [0.07,3.21],[0.06,3.19],[0.92,4.63],[0.71,4.29],[0.01,3.08],
    [0.33,3.44],[0.04,3.16],[0.21,3.36],[0.61,3.99],[0.54,3.89]
]

#生成X和y矩阵
dataMat = np.array(data)
X = dataMat[:,0:1]   # 变量x
y = dataMat[:,1]   #变量y

# ========线性回归========
model = LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
model.fit(X, y)   # 线性回归建模
print('系数矩阵:\n',model.coef_)
print('线性回归模型:\n',model)
# 使用模型预测
predicted = model.predict(X)

plt.scatter(X, y, marker='x')
plt.plot(X, predicted,c='r')

plt.xlabel("x")
plt.ylabel("y")
plt.show()